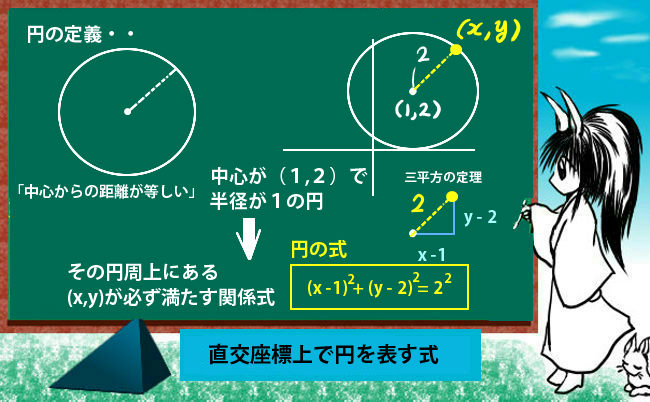
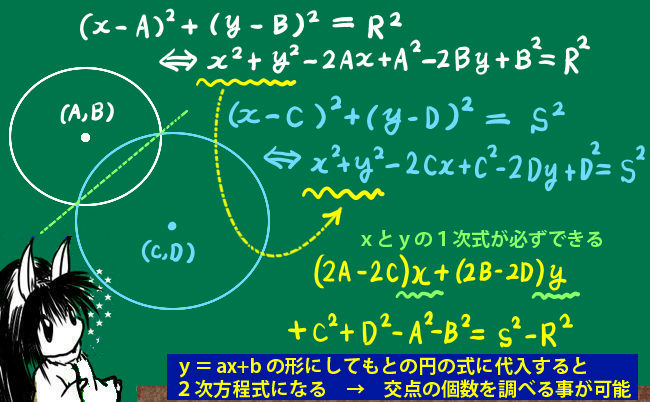
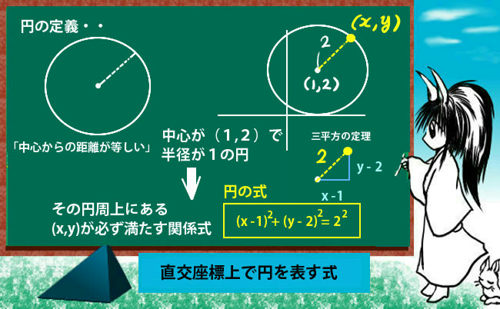
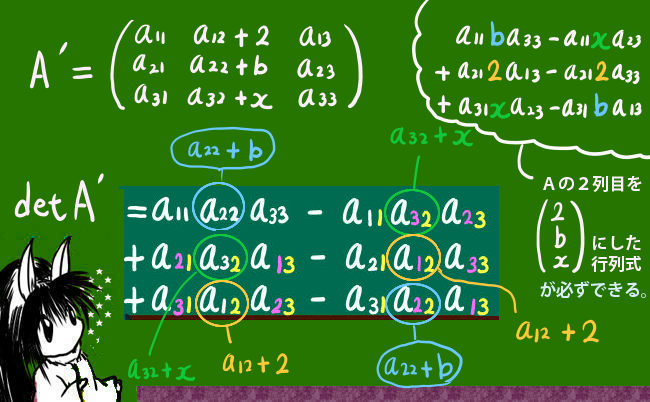行列式について成立する基本公式をまとめてます。
一般のn次の行列式の定義だけでも大変面倒であるわけですが、ここで述べる公式によって特定の条件のもとでの行列式の値を計算するのが容易になる、行列式を含む理論計算が簡易になる等の利点があります。
行列式については、次のような基本性質が成立します。扱う行列は全て正方行列とします。
- 列ベクトルに対する線型性
- 1つの列ベクトルが和・差の形の行列の行列式は和・差の形に分解できる。
- 行列式の1つの列に定数を乗じたものは全体にその定数を乗じた値に等しい。
- 2つ以上の列における和・差・定数倍に関しても所定の規則で行列式を分割できる。
- 列の置換に関する性質
- 列を置換した行列の行列式は、もとの行列式にその置換の符号を乗じたものに等しい。
- 行列式の中に全く同じ要素が並ぶ列が2つあれば行列式は0になる。
- 積に関する性質
- 行列の積に対する行列式は、個々の行列の行列式の積になる。
- 逆行列の行列式と、もとの行列の行列式の積は1に等しい。
(これらのうち、列に関する性質は行についても同様に成立します。)
尚、高校数学の範囲や、行列の理論を限定的にのみ使う工学等の分野で2次の正方行列や3次の正方行列のみを扱う場合には、上記の公式は全て行列の成分の直接計算で示す事ができます。(2次の場合は計算は簡単ですが、一般性は分かりにくいでしょう。)
よく使われる行列の簡易表記として、行列の列の部分を一括して「列ベクトル」とみなすやり方があります。例えば3次の正方行列であれば次のように表す感じです。
$$\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) =(\overrightarrow{a_1},\overrightarrow{a_2},\overrightarrow{a_3})$$
$$\overrightarrow{a_1}=\left(\begin{array}{ccc} a_{11} \\ a_{21}\\ a_{31} \end{array}\right),\hspace{10pt} \overrightarrow{a_2}=\left(\begin{array}{ccc} a_{12} \\ a_{22}\\ a_{32} \end{array}\right),\hspace{10pt}\overrightarrow{a_3}=\left(\begin{array}{ccc} a_{13} \\ a_{23}\\ a_{33} \end{array}\right)$$
以下、証明も含めて詳しく見てみきましょう。
列ベクトルに対する線型性
■
式による表現(1つの列の場合) ■
証明 ■
一般の列ベクトルに対する線型性
式による表現(1つの列の場合)
次のように、行列式の「列ベクトルに関する線型性」が成立します。c は定数(実数、複素数)とします。
$$A=(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k},\cdots\overrightarrow{a_n})\hspace{5pt}のとき、$$
行列式の列ベクトルに対する線型性
- 列ベクトルが和・差の形の行列の行列式は和・差の形に分解できる。$$\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k}+\overrightarrow{b_k},\cdots\overrightarrow{a_n})=\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k},\cdots ,\overrightarrow{a_n})+\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{b_k},\cdots ,\overrightarrow{a_n})$$
- 行列式の1つの列に定数を乗じたものは全体にその定数を乗じた値に等しい。$$\mathrm{det}(\overrightarrow{a_1},\cdots ,c\overrightarrow{a_k},\cdots ,\overrightarrow{a_n})=c\hspace{3pt}\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k},\cdots ,\overrightarrow{a_n})=c\hspace{3pt}\mathrm{det}A$$
和と差に関する性質のところは、「もとの行列と『1つの列だけ』別の列ベクトルに入れ替えた行列」の
行列式の和や差になるという事です。
列ごとの和になっているとか列ごと定数倍になっているとかいうのは、具体的には3次の正方行列で言うと次のような事です。
$$\mathrm{det}\left(\begin{array}{ccc} a_{11}+1 & a_{12} & a_{13}\\ a_{21} +3 & a_{22}& a_{23} \\ a_{31}-2 & a_{32} & a_{33}\end{array}\right) =\mathrm{det}\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) +\mathrm{det}\left(\begin{array}{ccc}
1 & a_{12} & a_{13}\\
3 & a_{22} & a_{23} \\ -2 & a_{32} & a_{33}\end{array}\right) $$
$$\mathrm{det}\left(\begin{array}{ccc} a_{11} & 4a_{12} & a_{13}\\ a_{21}& 4a_{22}& a_{23} \\ a_{31} & 4a_{32} & a_{33}\end{array}\right) =4\hspace{3pt}\mathrm{det}\left(\begin{array}{ccc}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) $$
証明
列ベクトルに関する線型性は、要するに行列式を構成する各項には1つの列の要素が必ず入っている事に起因します。
$$\mathrm{det}A = \sum_{\sigma}\mathrm{sgn(\sigma)}\left(\prod_{i=1}^na_{\sigma(i)i}\right) $$
行列式は行列の成分を使うとこのように表せるので、式で示す場合には次のようになります。
まず和・差のほうから見ると、あるk列目のそれぞれの行の成分に何らかの数が加えられている状況なので、積になっている部分のk番目のところだけを和の形にすればよい事になります。
すると全体を2つの和に分けて、それぞれ行列式の形になるというわけです。
$$\sum_{\sigma}\left\{\mathrm{sgn(\sigma)}\cdot a_{\sigma(1)1}a_{\sigma(2)2}\cdots (a_{\sigma(k)k}+b_{\sigma(k)k})\cdots a_{\sigma(n)n}\right\}$$
$$=\sum_{\sigma}\left(\mathrm{sgn(\sigma)}\cdot a_{\sigma(1)1}a_{\sigma(2)2}\cdots a_{\sigma(k)k}\cdots a_{\sigma(n)n}\right)+\sum_{\sigma}\left(\mathrm{sgn(\sigma)}\cdot a_{\sigma(1)1}a_{\sigma(2)2}\cdots b_{\sigma(k)k}\cdots a_{\sigma(n)n}\right)$$
結果の式では、積のk番目のところだけが別々になって2つの和になっています。
(積の部分は、積の記号\(\Pi\)を使用せずに直接各項を書き下す形にしています。省略部分「・・・」のところは掛け算が続きます。)
定数倍のほうも同じで、積のk番目のところがc倍で、これは和全体に乗じられる定数倍とみなせます。
$$\sum_{\sigma}\left(\mathrm{sgn(\sigma)}\cdot a_{\sigma(1)1}a_{\sigma(2)2}\cdots ca_{\sigma(k)k}\cdots a_{\sigma(n)n}\right)=c \sum_{\sigma}\left(\mathrm{sgn(\sigma)}\cdot a_{\sigma(1)1}a_{\sigma(2)2}\cdots a_{\sigma(k)k}\cdots a_{\sigma(n)n}\right)$$
一般の列ベクトルに対する線型性
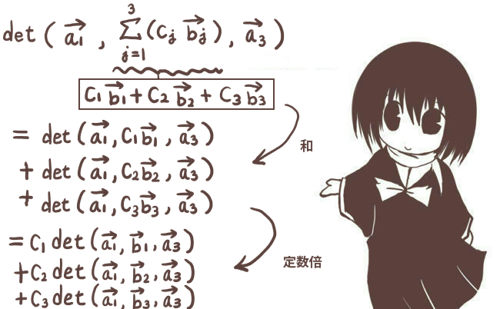
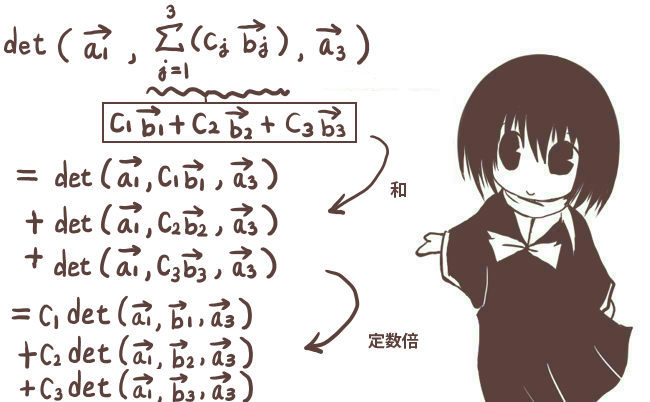
1箇所の列ベクトルについて和や定数倍の項が増えた時には線型性の式を繰り返し使って、
シグマ記号を使って1つにまとめる事もできます。
これは、1つの列のところについて \(c_1\overrightarrow{a}+c_2\overrightarrow{b}+c_3\overrightarrow{d}\) のようになっている場合です。
2箇所以上の列ベクトルで和や差の形になっている場合は少し注意が必要です。1箇所だけのときの証明のやり方を見てもらうと分かりやすいと思うのですが、2箇所ある場合には行列式は2項に分かれるのではなく、2×2=4項に分かれます。n箇所に2項ずつある場合には2n項に分かれます。これを直接書くのは大変面倒ですが、シグマ記号を使うとより簡潔に表せます。
行列式の線型性・一般の場合
- 1つの列ベクトルにおける一般の場合:$$\mathrm{det}\left(
\overrightarrow{a_1},\cdots ,\sum_{j=1}^m(c_j\overrightarrow{b_j}),\cdots\overrightarrow{a_n}
\right)=\sum_{j=1}^mc_j
\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{b_j}\cdots ,\overrightarrow{a_n})$$
- 2つ以上の列ベクトルにおける一般の場合
$$\mathrm{det}
\left(
\overrightarrow{a_1},\cdots ,\sum_{i=1}^{m1}(c_{pi}\overrightarrow{b_{pi}}),\cdots ,\sum_{j=1}^{m2}(c_{sj}\overrightarrow{b_{sj}}),\cdots ,\sum_{k=1}^{m3}(c_{tk}\overrightarrow{b_{tk}}),\cdots\overrightarrow{a_n}
\right)$$
$$=\sum_{i,j,k \cdots =1}^{m1,m2,m3,\cdots}c_{ki}c_{pj}c_{tk}
\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{b_{pi}},\cdots ,\overrightarrow{b_{sj}},\cdots,\overrightarrow{b_{tk}},\cdots,\overrightarrow{a_n})$$
2番目のほうの式の和の記号のところは、i,j,k,・・のそれぞれについて、
1~m1、1~m2、1~m3、・・まで動かすという意味です。
そのため、和の項数は合計でそれぞれを掛け合わせたm1m2m3・・個 になります。
一般的に手計算では手に負えない事は見て明白だと思うので、「形」を把握しましょう。
例として、2箇所の列ベクトルについて2項ずつの和になっている時は、要するに行列式を表す積の中の2箇所で (a1+b)(a2+c)=a1a2+a1b+a2c+bcの形になるので4つに分割されるという事です。
もし3箇所の列ベクトルについて2項の和になっているのであれば23=8つに分割されます。
2箇所の場合について証明の式を具体的に書くと次のようになります。
途中で「・・・」で略してる部分は全て掛け算が続いています。
$$\sum_{\sigma}\left\{\mathrm{sgn(\sigma)}\cdot a_{\sigma(1)1}a_{\sigma(2)2}\cdots (a_{\sigma(k)k}+b_{\sigma(k)k})\cdots(a_{\sigma(m)m}+d_{\sigma(m)m})\cdots a_{\sigma(n)n}\right\}$$
$$=\sum_{\sigma}\left(\mathrm{sgn(\sigma)} a_{\sigma(1)1}\cdots a_{\sigma(k)k}\cdots a_{\sigma(m)m}\cdots a_{\sigma(n)n}\right)
+\sum_{\sigma}\left(\mathrm{sgn(\sigma)} a_{\sigma(1)1}\cdots b_{\sigma(k)k}\cdots a_{\sigma(m)m}\cdots a_{\sigma(n)n}\right)$$
$$+\sum_{\sigma}\left(\mathrm{sgn(\sigma)} a_{\sigma(1)1}\cdots a_{\sigma(k)k}\cdots d_{\sigma(m)m}\cdots a_{\sigma(n)n}\right)+\sum_{\sigma}\left(\mathrm{sgn(\sigma)} a_{\sigma(1)1}\cdots b_{\sigma(k)k}\cdots d_{\sigma(m)m}\cdots a_{\sigma(n)n}\right)$$
このように、4つに分割されるわけです。
列の置換に対する性質
■ 式による表現 ■ 証明(列の置換) ■ 証明(同一の列が2つ以上の時)
式による表現
行列の特定の列と別の要素を入れ替えたり、列の順番を並び替えたした行列の行列式は、もとの行列の行列式と絶対値は必ず同じであり符号だけが異なるという結論になります。
その性質の派生物として、行列内の2つの列ベクトルの要素の値が全く等しい場合には行列式の値は必ずゼロになるという結果も示せます。
列の置換に関連する行列式の性質
- 列を置換 \(\tau\) によって並び替えた行列の行列式は、
もとの行列式にその置換の符号 \(\mathrm{sgn}(\tau )\) を乗じたものに等しい。
$$\mathrm{det}(\overrightarrow{a}_{\large{\tau (1)}},\cdots ,\overrightarrow{a}_{\large{\tau (k)}},\cdots\overrightarrow{a}_{\large{\tau (n)}}) =\mathrm{sgn}(\tau) \mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k},\cdots ,\overrightarrow{a_n})$$
- 正方行列の異なる2つの列ベクトルについて \(\overrightarrow{a_k}=\overrightarrow{a_m}\) となるk、mが存在するならば
その行列式の値は必ず0になる。
$$A=(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k},\cdots ,\overrightarrow{a_m},\cdots,\overrightarrow{a_n})で、\overrightarrow{a_k}=\overrightarrow{a_m}となる時$$
$$\mathrm{det}=0$$
これは理屈としては難しくないのですが、式による証明では少々込み入ります。ここで挙げている行列式の公式の証明の中では最も難しく、しかし重要(積に関する性質の証明に必要なため)という厄介な箇所です。
例えば、1列目と2列目を入れ替えた場合、互換の符号はマイナスなので行列式は「もとの行列式にマイナス符号をつけたもの」になります。
$$\mathrm{det}\left(\begin{array}{ccc} a_{12} & a_{11} & a_{13}\\ a_{22} & a_{21} & a_{23} \\ a_{32} & a_{31} & a_{33}\end{array}\right) =-\mathrm{det}\left(\begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right) $$
2つの列の要素が全く同じ場合とは、2つの列について1行目の値が互いに同じ、2行目の値も互いに同じ、・・・以下、何行目であっても全部互いに等しいという事です。この時、行列式の値はゼロになります。証明を見ると分かる通り、じつはこの性質は列ベクトルの置換に関係します。
$$\mathrm{det}\left(\begin{array}{ccc} 2 & 2 & a_{13}\\ 5 & 5 & a_{23} \\ 1 &1 & a_{33}\end{array}\right)=0 $$
証明(列の置換)
置換 \(\tau\) によって列ベクトルの要素が並び替えされている時、逆置換(より一般的には逆写像)に相当する \(\tau\)-1 を考える事が1つの重要ポイントです。
これは、例えば(1→2, 2→3, 3→1)という置換を逆にたどった(2→1, 3→2, 1→3)の事です。
【1つの例】
\(\tau\) :1→2, 2→3, 3→1
\(\tau\)-1:2→1, 3→2, 1→3
さてしかし、そんなものをなぜ唐突に考えるのかというと、もちろん理由はあります。
まず、\(\tau\) によって列の配列が変わっている行列A’ の成分をbijとおきます。
この置き換えの文字を使うと、行列式はとりあえず通常の形で表せます。
この段階では置換\(\tau\) はまだ式の中には出てきません。
$$\mathrm{det}A^{\prime} = \sum_{\sigma}\mathrm{sgn(\sigma)}\left(\prod_{j=1}^nb_{\sigma (j)j}\right)$$
ここで、列だけ入れ替えて行はいじっていないという設定なので、行列成分bijの添え字の列部分だけを 置換\(\tau\) で変化させるともとの行列成分の形に直す事が可能で、次のように表せます。
$$\large{b_{\sigma (j)j}=a_{\sigma (j)\tau (j)}}$$
これは例えば1列目と2列目が入れ替わっていて、入れ替えたあとの2行1列目を考える時、そこにある要素をbijで表すとb21ですがもとのaijで表すなら列が入れ替わってますからa12になるという意味です。今の例ではb21=a12 であり、\(\tau\)(1)=2です。
式で表すとかなり分かりにくいかと思いますが、bijの積をaijで表した時に、
「列の順番が左から1,2,3・・になるように」書き換える事ができます。
例えば、a22a31a13という積はa31a22a13と書いても同じ値であるという意味です。
つまり、\(\large{b_{\sigma (j)j}=a_{\sigma (j)\tau (j)}}\) において、
「積の並び替え」をする事で \(\tau (j)\) の部分はjに書き換える事が可能である「はず」です。
列を順序通りに「並び替え」するという事は「列の番号の置換」を行うと見なす事もできます。
しかもここでは「置換\(\tau\)」によって配列が変わったものを「もとに戻しているという」操作に相当するので、
積の順序並び替えに相当する置換は列に関しては \(\tau\) の逆置換である \(\tau\)-1になるのです。
しかしその場合、行の番号はどう表すのかという話になります。これは、次のようにします。
aijの列の番号から\(\tau\)-1でbijの列の番号をたどり、そこに\(\sigma\)を作用させて行の番号を得ます。
aijで見た時の列の番号がkのとき、これのもとになっていたbijの列の番号は\(\tau\)-1(k) ですが、
行の番号はそれをさらに置換 \(\sigma\) で変えて \(\sigma\)( \(\tau\)-1(k) ) = \(\sigma\) \(\tau\)-1(k) となるという事です。
少し分かりにくいパズルかもしれませんが、\(\large{b_{\sigma (j)j}}\) の行部分は、列の番号を基準にして何に置き換わったかを指しています。例えばb22に対してb32のようなものを考えるわけです。
つまり、bijの列の番号が分かればi= \(\sigma\)(j) という具合に行の番号が判明します。
aijとbijとでは列の置換だけがなされて行はいじっていないのでbijのほうの行の番号が分かればそれがaijの行の番号に一致する、という事です。
そこで、行列式は次のように変形できるという事になります。
$$\mathrm{det}A^{\prime} = \sum_{\sigma}\mathrm{sgn(\sigma)}\left(\prod_{j=1}^nb_{\sigma (j)j}\right)=\sum_{\sigma}\mathrm{sgn(\sigma)}\left(\prod_{j=1}^na_{\sigma \tau ^{-1}(j)j}\right)$$
ここで、sgn(\(\sigma\))=sgn(\(\sigma \tau ^{-1}\tau\))=sgn(\(\sigma \tau ^{-1}\))sgn(\(\tau\)) と変形できる事に注意します。
また、\(\sigma \tau ^{-1}\) という写像も置換であり(\(\sigma \) を動かす事で)n次の置換の要素全てに対応しています。
という事は、次のようにもとの行列Aの行列式を含んだ形に式を変形できるという事です。
$$\mathrm{det}A^{\prime} =\sum_{\sigma}\mathrm{sgn(\sigma)}\left(\prod_{j=1}^nb_{\large{\sigma \tau ^{-1}(j)j}}\right)=\sum_{\large{\sigma \tau ^{-1}}}\mathrm{sgn(\sigma)}\left(\prod_{j=1}^na_{\large{\sigma \tau ^{-1}(j)j}}\right)$$
$$=\sum_{\large{\sigma \tau ^{-1}}}\mathrm{sgn}(\sigma \tau ^{-1})\mathrm{sgn}(\tau)\left(\prod_{j=1}^na_{\large{\sigma \tau ^{-1}(j)j}}\right)$$
$$=\mathrm{sgn}(\tau)\sum_{\large{\sigma \tau ^{-1}}}\mathrm{sgn}(\sigma \tau ^{-1})\left(\prod_{j=1}^na_{\large{\sigma \tau ^{-1}(j)j}}\right)$$
$$=\mathrm{sgn}(\tau)\mathrm{det}A$$
和の記号の中で\(\sigma\) は置換全体を動かしますが、\(\tau\) はある特定の「1つの置換」です。
(例えば前述の例のように\(\tau\):1→2, 2→3, 3→1)
そのため、sgn(\(\tau\) ) はシグマ記号に乗じる形にできて、残った部分は(合計で)Aの行列式に等しくなります。
証明(同一の列が2つ以上の時)
上記の関係式が成立するのであれば、もしも互いに一致する列ベクトルが2つ以上あった場合には行列式の値が0になる事を示せます。
k列目とm列目が等しくなる時、この2列だけを入れ替えた行列式は、もとの行列式にマイナス符号をつけたものになります。(互換の符号はマイナス。)
$$すると、\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k},\cdots \overrightarrow{a_m},\cdots\overrightarrow{a_n})=-\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{a_m},\cdots \overrightarrow{a_k},\cdots\overrightarrow{a_n})より、$$
$$\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k},\cdots \overrightarrow{a_k},\cdots\overrightarrow{a_n})=-\mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k},\cdots \overrightarrow{a_k},\cdots\overrightarrow{a_n})$$
$$\Leftrightarrow \mathrm{det}(\overrightarrow{a_1},\cdots ,\overrightarrow{a_k},\cdots \overrightarrow{a_k},\cdots\overrightarrow{a_n})=0$$
ここで使っているのは、実数(あるいは複素数でも)について符号がプラスでもマイナスでも同じ値になる数、「x=-x」が成立する数は0だけであるという事を使っています。
積に関する性質
■ 式による表現 ■ 証明(行列の積に対する行列式) ■ 証明(逆行列の行列式)
式による表現
2つの行列AとBの積ABに対して、行列式 det(AB) はどのような値になるでしょう?普通に考えるといかにも収拾のつかない複雑な式になりそうですが(実際、直接計算すると手に負えません)、これはAの行列式とBの行列式の積になるのです。
その結論の派生物の1つとして、『逆行列の行列式』=1/『もとの行列式』という公式を導出できます。また、逆行列の存在の可否と行列式の値の関係の一部についても分かります。
積に関する行列式の性質
- 行列の積に対する行列式は、個々の行列の行列式の積になる。
$$\mathrm{det}(AB)=(\mathrm{det}A)\hspace{3pt}(\mathrm{det}B)$$
- 逆行列の行列式と、もとの行列の行列式の積は1に等しい。
$$\mathrm{det}A\hspace{3pt}\mathrm{det}(A^{-1})=1$$
2番目のほうの性質は「Aの逆行列が存在するならば」という前提です。
(最後に触れますが、そもそも逆行列が存在しない場合があり得るためです。)
結果自体はシンプルですが、証明はやや込み入ります。
ただし、前述の列ベクトルの線型性や、置換に関して成立する関係式を使うと証明可能です。
証明(行列の積に対する行列式)
「行列の積に対する行列式」の状況を調べる時、定義通りに要素の計算をすると一般のn次の正方行列に対しては非常に面倒な式になってしまうので工夫が必要です。
ABの1行1列目の要素はa11b11+a12b21+a13b31+・・・+a1nbn1 で、2行1列目の要素はa21b11+a22b21+a23b31+・・・+a2nbn1のようになりますが、同一の列で見た場合、Bの要素の1列目は共通して使い回されています。これを利用して、まずABの要素を列ごとに整理します。
ABの1列目の要素を列ベクトルで表す事ができて、次のようになります。
$$b_{11}\left(\begin{array}{ccc} a_{11} \\ a_{21}\\\cdots\\ a_{n1} \end{array}\right)+b_{21}\left(\begin{array}{ccc} a_{12} \\ a_{22}\\\cdots\\ a_{n2} \end{array}\right)+\cdots +b_{n1}\left(\begin{array}{ccc} a_{1n} \\ a_{2n}\\\cdots\\ a_{nn} \end{array}\right) =b_{11}\overrightarrow{a_1}+b_{21}\overrightarrow{a_2}+\cdots +b_{n1}\overrightarrow{a_3}=\sum_{j=1}^{n}(b_{j1}\overrightarrow{a_j})$$
そこで、AB全体を列ベクトル表記すると次のようになります。
省略している「・・・」の部分にもシグマ記号で表された各列ベクトルがあります。
$$AB=\left(\sum_{j=1}^{n}(b_{j1}\overrightarrow{a_j}),\hspace{5pt}\sum_{k=1}^{n}(b_{k2}\overrightarrow{a_k}),\cdots,\hspace{5pt}\sum_{z=1}^{n}(b_{zn}\overrightarrow{a_z})\right)$$
これの行列式を、一般の場合の列ベクトルの線型性によって分割します。
この場合には、各列に関して「全く同じ要素を持つ列」になる項が含まれます。
例えば、上記でj=1のときとk=1のときでは全く同じ形の \(\overrightarrow{a_1}\) の形が1列目と2列目に生じます。
(定数倍は行列式全体に掛ける形になるので、この件に関して影響を与えません。)
すると、その部分の行列式の項は0になります。
そのため、和の記号のj, k, ・・・,zの部分は、必ずそれぞれ違う番号を代入した項だけが残るわけです。
j, k, ・・・,zのそれぞれは1~nの範囲を動く事は共通しており、
j, k, ・・・,zの個数自体もn個ある事に注意します。
すると、j, k, ・・・,zの中身は、1~nの番号を置換したものになるのです。
これは、和をとるときに各々1~nではなく、
j, k, ・・・,z全体で「1~nの番号の『置換』」に渡って動くと捉えてよい事を意味します。
具体的に、n=4の場合、各列のシグマ記号の変数について例えば(i,j,k,z)=(2,3,4,1) のような組み合わせの項だけが残ります。(i,j,k,z)=(3,3,4,1)のようになる場合は、その行列式の項は0になるので考えなくていいという事です。
すると、上式の行列式は次のように書けるのです。
$$\mathrm{det}(AB)=\large{
\sum_{j,k,\cdots z=1}^{それぞれnまで}
\left\{
b_{j1}b_{k2}\cdots b_{zn}\mathrm{det}(\overrightarrow{a_j},\overrightarrow{a_k},\cdots,\overrightarrow{a_z})
\right\}
}$$
$$=\large{
\sum_{\sigma}
\left\{
\left(\prod_i^n b_{\sigma (i)i}\right)
\mathrm{det}
(\overrightarrow{a}_{\sigma (1)} ,
\overrightarrow{a}_{\sigma (2)} ,
\overrightarrow{a}_{\sigma (3)} ,
\cdots ,
\overrightarrow{a}_{\sigma (n)})
\right\}
}
$$
$$=\large{
\sum_{\sigma}
\left\{
\left(\prod_i^n b_{\sigma (i)i}\right)
\mathrm{sgn}(\sigma)
\mathrm{det}
(\overrightarrow{a}_1 ,
\overrightarrow{a}_2 ,
\overrightarrow{a}_3 ,
\cdots ,
\overrightarrow{a}_n)
\right\}
}$$
$$=\large{
\sum_{\sigma}
\left\{
\left(\prod_i^n b_{\sigma (i)i}\right)
\mathrm{sgn}(\sigma)
\mathrm{det}A
\right\}
}$$
$$=\large{ (\mathrm{det}A) \sum_{\sigma} \left\{ \mathrm{sgn}(\sigma) \left( \prod_i^n b_{\sigma (i)i} \right) \right\} }$$
$$=\large{ (\mathrm{det}A)( \mathrm{det}B) }$$
このようにして det(AB)=(detA) (detB) が確かに成立する事になります。
証明(逆行列の行列式)
上記の性質を単位行列に適用する事で、逆行列に関する行列式の関係式も分かります。
すなわち、単位行列IはI=A(A-1)と表せて、単位行列の行列式の値は1になるので detI=det{A(A-1)}= det A det A-1 ⇔ 1=det A det A-1
このとき、もちろん行列式が0でないという前提はあります。
あるいはむしろ、
ある行列が可逆(逆行列が存在する)ならば、
I=A(A-1) ⇔ 1=det A det A-1
となるので必ず det A≠0である、と言う事もできます。
「正方行列Aが可逆である(逆行列が存在する) ⇒ det A≠0」という事です。
その対偶命題をとると、
「detA=0ならば行列Aは可逆でない(逆行列は存在しない)」という事も分かります。
では「detA≠0ならばAは可逆で逆行列が存在する」という命題はどうかというと、結論から言うとこれも成立しますがこれまでの議論ではここまではまだ示せません。(もう一工夫必要で、余因子行列というものと行列式の関係を調べる事で証明できます。)
逆行列と可逆性の関係
結論を言うと次の同値関係が成立します。
「detA≠0 ⇔ 正方行列Aは可逆で、逆行列A-1が存在する。」
(detA=0ならばAは可逆でなく、逆行列は存在しない。)