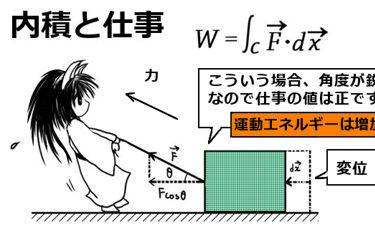
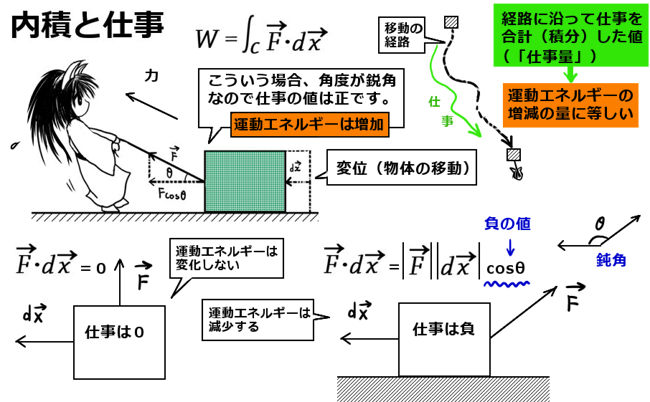
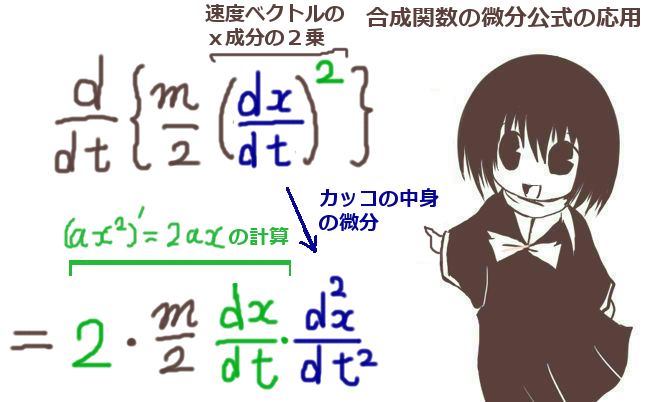
微分が「傾き」を表すのに対し、積分は「面積」を表すというのが基本的な考え方です。
(使い方は色々あって、「体積」を表す事もできます。また、後述するように通常の図形問題で言う面積との相違点もあります。)
英:積分 integral 定積分 definite integral
考え方と計算方法
関数y=f(x)の微分係数はxの各点ごとに1つ、傾きの値として決まります。これに対して、積分の場合にはxの2点を指定するごとに面積の値として決まります。この2点で挟まれる閉区間は積分区間と呼ばれます。この面積は、f(x)を表す曲線とx軸、指定した2点を通りx軸に垂直な直線で囲まれる面積です。
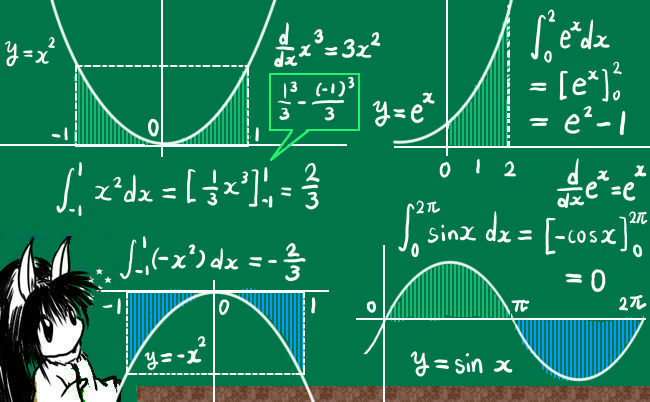
この面積の計算が積分で、このように定まった積分区間内の面積の値は特に「定積分」と呼ばれます。
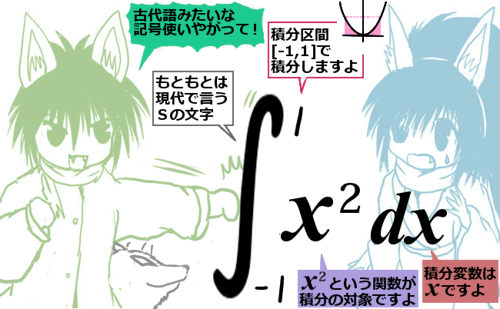
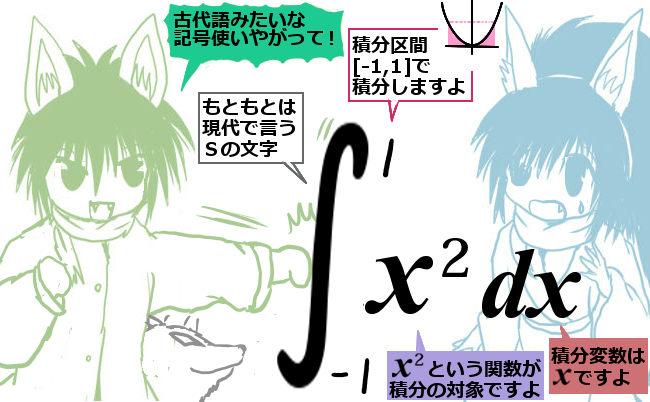
積分区間 [a,b] における関数y=f(x)に対する定積分は、記号では次のように書きます。
「定積分」を次のように書きます。この計算をする事を「積分する」とも言います。$$\large{\int_a^bf(x)dx}$$
- \(\int\) の記号はSの文字由来と言われる。(「和」「合計」を表す語の頭文字)
- 上下に添えられた文字は積分区間 [a,b] の事
- dxは対象の関数の変数がxである事を表す。
【dxと書く由来は微小な区間の幅dxをf(x)に乗じて合計し面積を近似しているため】
定積分の値は1であるとか2であるとか、何らかの「値」になります。
(f(x)が負であれば定積分の値は負の数になる事もあり、0でもあり得ます。)
f(x)に具体的な関数を入れて、特定の積分区間の定積分を考えます。$$\int_{-1}^1x^2dx\hspace{15pt}\int_{0}^2e^xdx\hspace{15pt}\int_{0}^{\large{\pi}}\cos xdx\hspace{15pt}\int_{1}^{\large{e}}\ln xdx$$
次に、具体的にどういう計算をすればよいかという話になります。
結論を先に言うと次の手順で定積分は計算できます。
- 微分すると「対象の関数f(x)になる」別の関数F(x) を探す。
【例えば f(x)=x2 であればF(x)=x3/3, f(x)=cosxであればF(x)=sinx】 - 積分区間 [a,b] のa、bをF(x)に代入したものを用意する。
【例えば積分区間 [0,1]で F(x)=x3/3 であればF(0)=0とF(1)=1/3を用意】 - F(b)-F(a)を計算する。これが積分区間 [a,b] でのf(x)の定積分の値になる。
【例えばF(1)-F(0)=1/3-0=1/3になる。】 $$\left(この計算の時に、F(b)-F(a)を\left[F(x)\right]_a^bとよく書きます。\right)$$
「微分するとf(x)になる」別の関数F(x)の事を、原始関数とも言います。
このように計算できる事は、微積分学の基本定理がもとになっています。
基本的な考え方としては、x軸とy軸、x軸上の1点 (x,0) に垂直な直線とy=f(x) の曲線で囲まれる面積をS(x)として、微分の定義式に当てはめるとS(x)を微分して得られる導関数(d/dx)S(x)=f(x) となるというものです。これはy軸、すなわちx=0から始めているので、S(b)からS(a)を差し引けば閉区間 [a,b] における面積となるという事です。

この時、微分方程式を解く時の注意点にも共通しますが、ある関数F(x)を微分してf(x)になる時、定数cを加えたF(x)+cという関数も同様に「微分するとf(x)になる」関数になります。定積分を計算する時にF(b)-F(a)という引き算を考えるのは、その不定の定数を除去して面積の値を確定させるという工夫です。
具体的な計算例
y=x2の積分区間 [-1,1] での定積分は次のように計算します。
$$\int_{-1}^1x^2dx=\left[\frac{1}{3}x^3\right]_{-1}^1=\frac{1}{3}-\frac{-1}{3}=\frac{2}{3}$$
この計算では、1/3という係数がくっつけて【x3を微分すると3x2なので3で割る】、最後の引き算を考える時に―1をx3/3に代入し、それをさらに「引き算する」ので符号はプラスになり、結果的に2つの正の数の値を加える形になっています。
$$\int_{0}^2e^xdx=\left[\large{e^x}\right]_0^2=e^2-1$$
$$\int_{0}^{\large{2\pi}}\sin xdx=-\left[\large{\cos x}\right]_0^{\large{2\pi}}=-(1-1)=0$$
微分すると sinxになる関数は-cosxですが、ここでは符号の煩雑さを避けるために積分区間の端点(\(2\pi\) と0)を代入するところでカッコの外にマイナス符号を出しています。このような操作は、符号も含めて定数倍に関しては一般的に行う事ができる操作です。
なお、この定積分の計算を1次関数(図形的には直線)に適用すると、きちんと「三角形の面積公式」で計算した時と同じ結果を得ます。
$$\int_0^3xdx=\frac{1}{2}[3x^2]_0^1=\frac{3}{2}(1-0)=\frac{3}{2}$$
$$底辺×高さ÷2で計算して\hspace{5pt}\frac{1\cdot 3}{2}=\frac{3}{2}\hspace{5pt}でも同じ$$

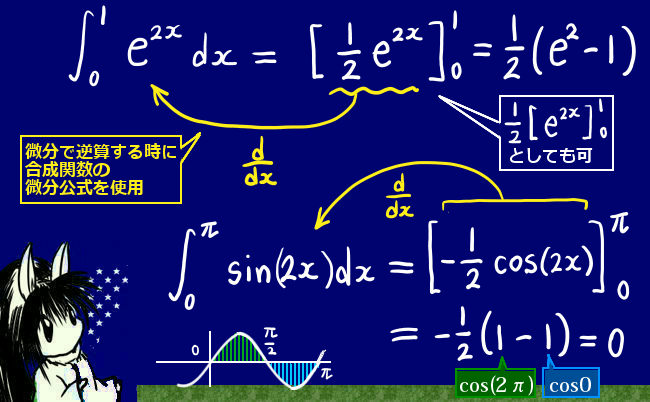
個々の関数に関してどのように定積分を計算するかは結局のところ微分の問題になる事も多く、合成関数の微分などを使用する事もあります。三角関数の場合には加法定理などを使って工夫してから定積分を計算すると分かりやすい事もあります。
$$\int_0^1e^{2x}=\left[\frac{1}{2}e^{2x}\right]_0^1=\frac{1}{2}\left(e^2-1\right)$$
$$\int_0^{\pi}(\cos x\sin x)dx=\frac{1}{2}\int_0^{\pi}\sin (2x)dx=-\frac{1}{4}\left[\cos (2x)\right]_0^{\pi}=-\frac{1}{4}(1-1)=0$$
$$\int_{1}^{\large{e}}\ln xdx=\int_{1}^{\large{e}}\left[x\ln x-x\right]_{1}^{\large{e}}=(e\ln e-e)-(1\cdot 0-1)=(e-e)-(-1)=1 $$
【(d/dx)(xlnx-x)=lnx+x/x-1=lnx+1-1=lnx 積の微分公式使用】
y軸に関して対称な関数(偶関数)の定積分を [-a,a] で考える時は[0,a]での定積分の2倍の値を考えればよく、原点に対して点対称な関数(奇関数)の定積分を [-a,a] で考える場合は値は必ず0になります。
上記の例でも、積分区間が[-a,a]の形であれば偶関数・奇関数の性質を使って計算できるものもあります。
定積分は「負の値」やゼロの事もある
関数が負の値になる時も、定積分はそのまま計算するルールになっています。
y=-x2のような関数を積分区間 [-1,1] で積分する時は、定積分の結果は負の値になります。
$$\int_{-1}^1(-x^2)dx=\left[-\frac{1}{3}x^3\right]_{-1}^1=-\frac{1}{3}-\left(-\frac{-1}{3}\right)=-\frac{2}{3}$$
こういうとき、マイナス符号の扱いが煩雑になりがちなので、計算しやすいように工夫したほうがよい事もあります。例えばこの場合には「y=x2の同じ積分区間での定積分にマイナス符号をつければよい」事になるので、次のようにも書けます。
$$\int_{-1}^1(-x^2)dx=-\int_{-1}^1x^2dx=-\left[\frac{1}{3}x^3\right]_{-1}^1=-\left(\frac{1}{3}-\frac{-1}{3}\right)=-\frac{2}{3}$$
y=sinxの[0,\(2\pi\)] での定積分は0ですが、これは 0から\(\pi\)までの定積分の値がプラスで、そこから定積分はマイナスに転じます。それで、差し引きゼロになってしまうという事です。
$$\int_{0}^{\large{\pi} }\sin xdx=-\left[\large{\cos x}\right]_0^{\large{\pi}}=-(-1-1)=2\hspace{15pt}\int_{\large{\pi}}^{\large{2\pi} }\sin xdx=-\left[\large{\cos x}\right]_{\large{\pi}}^{\large{2\pi} }=-(1+1)=-2\hspace{15pt}$$
半周期の範囲で正弦関数とx軸で囲まれる面積がぴったりと整数になるのは意外かもしれませんが、とりあえず積分の計算によるとそういう結果になるという事です。
プラスとマイナスの両方の値を取り得るという意味では、定積分の計算は平面幾何での図形の「面積」と少し違っている事になります。
もし平面幾何の意味での「面積」の総和を出す必要があるなら、確実に計算するのであればy=f(x)が合った時には絶対値記号をつけて|y|=|f(x)|の定積分を計算します。つまり、負の部分は全てx軸に関してひっくり返して計算する事になります。
他に、関数の2乗を考える場合など、関数の値が確実にプラスである事が確定している時には定積分の計算結果は引かれている部分が無い「面積」の総和になります。