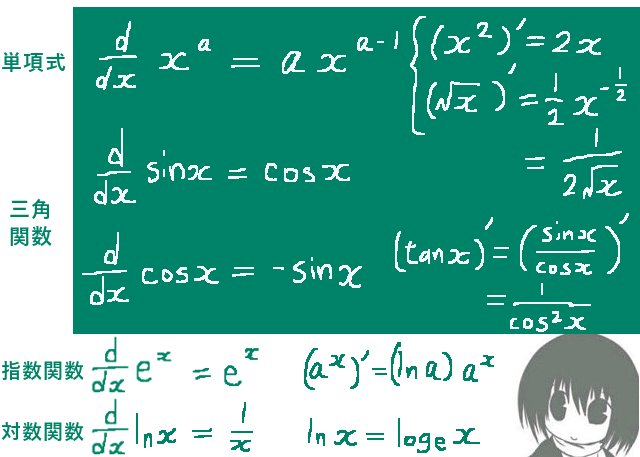大学の微積分学の入門として、簡単に解ける微分方程式について説明します。
微分方程式の解き方の手短な説明
微分方程式とはその通り、微分(および高階微分)を含んだ方程式ですが、要はその方程式を満たす「関数」を探す事が、その方程式を解くという事です。このページで紹介する微分方程式は、パズル感覚で色々組み合わせるだけで解けます。
声優担当:ステ♪様 http://sute.tabigeinin.com/
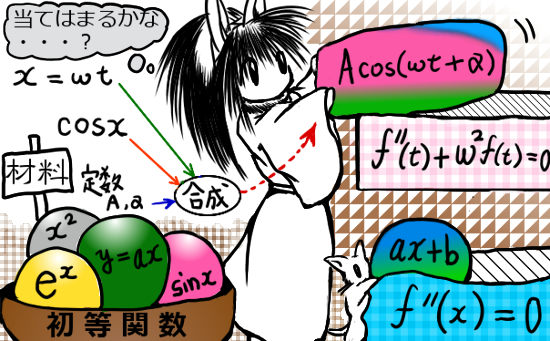
つまり、微分の公式 を微分方程式に当てはめてみて、確かに解になっていればよいわけです。微分の公式と言ってもたくさんあるわけですが、今回用いるのは6つで、三角関数に関しては正弦か余弦のどちらか片方あれば足りるので、実質「5つ」だけの公式を用います。それらは次の表にまとめてあります。これらを単独で使うか上手に組み合わせるかして、微分方程式を解いていけるのです。
合成関数も利用しながら、初等関数の「パーツ」を組み合わせ、具体的な微分方程式に当てはめてみます。このタイプの解法は、高校で教わる微分の知識を直接使えます。「2回微分すると〇○になる関数はどれですか」といった事について、公式の中から探して、組み合わせればよいのです。 使う公式は、この場で表にして記しておきましょう。
対象の関数 微分公式 微分方程式の解法での役割 ①定数(定数関数) \({\large \frac{d}{dx}c=0}\) 微分すると0になる ②単項式「x の a 乗」 \({\large \frac{d}{dx}x^a=ax^{a-1}}\) 微分するとx の指数が1下がる ③自然対数の底 e の指数関数 \({\large \frac{d}{dx}e^x=e^x}\) 微分すると元の関数に戻る ④-1 三角関数(正弦関数) \({\large \frac{d}{dx}\sin x=\cos x}\) 微分2回で元の関数の符号±入替 ④-2 三角関数(余弦関数) \({\large \frac{d}{dx}\cos x=-\sin x}\) 微分2回で元の関数の符号±入替 ⑤合成関数の微分 \({\large \frac{df(y)}{dx}=\frac{df(y)}{dy}\frac{dy(x)}{dx}}\) 微分方程式内の定数倍などを調整
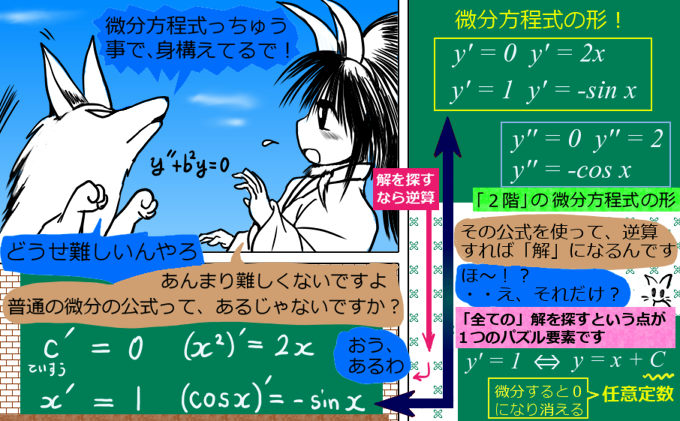
基本は、通常の微分の公式を用いて、当てはまる関数を見つけるだけです。微分方程式特有の考え方としては、「全ての」解を表現するという意味では「微分すると0になって消える定数項」などがオマケとして解にくっついてくる事です。(最初のうちはあまりこだわらなくていいと思います。)
微分方程式論の中の位置付け
このページでは「具体的な微分公式を探して当てはめてみる」という見方をしますが、このやり方は、じつは「微分の逆演算つまり積分 を行い『微分記号を消去する』事で、解となる関数を見つける」・・という見方と同等なのです。そのため、微分方程式論の枠組みの中では「求積法 」と呼ばれます。
少し発展事項
~微分方程式の「解」は、基本的に1つではなく「複数」ある~
具体的な関数を微分方程式に当てはめてみて、それで確かに式が成り立てば、その関数は間違いなく「解」の1つです。他方で、数学的に少し面倒で時に厳密な論証が必要なのは、「それで『全ての解』を表現できているか??」 という点にあります。その事も念頭に置きながら、具体例を通して少しずつ理解していくと学習しやすいかと思います。
では具体的な微分方程式を見てみましょう。とても簡単に、解けます。
①一番簡単な微分方程式「1階微分=0」f ‘(x)=0
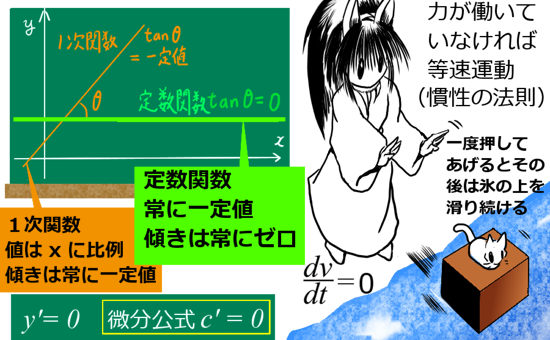
最初に見るのは、「1階微分(通常微分)がゼロになる」という微分方程式です。これは、即刻解けます。しかも、運動方程式において物理的な意味も持ちます。
①一番簡単なタイプの微分方程式
$$ \frac{d}{dx}f(x)=0$$
「微分すると0になる」関数はなんだろう、という方程式です。
$$解: 定数関数\hspace{5pt}f(x)=C \hspace{10pt}(C:定数)$$
当てはまるような公式を探してみますと、
対象の関数 微分公式 微分方程式の解法での役割 ①定数(定数関数) \({\large \frac{d}{dx}c=0}\) 微分すると0になる
と、いうものがありますね。
1つだけ注意していただきたいのは、0や1や2などの「特定の定数」だけではなく、定数であればどんなものでもよいという事です。その事を表現するために、「任意の定数」という表現を用います。この表現は、他のタイプの微分方程式の解でも用います。
物理の力学での運動方程式ではこのタイプの微分方程式は慣性の法則 のうち等速運動 である事を表現します。
② 2階微分=ゼロ f ”(x)=0 1次関数
2階微分が0になるという微分方程式も、簡単に解けるタイプのものです。高階の微分が入っていると一見難しく見えるかもしれませんが、これもじつは非常に簡単なのです。力が働いていない物体は等速「直線」運動する 事に関わります。
「2階微分=0」という微分方程式
$$ \frac{d^2}{dx^2}f(x)=0$$
「『2回』微分すると0になる」関数はなんだろう?という方程式です。
$$解: 1次関数\hspace{5pt}f(x)=bx+c\hspace{10pt}(b,c:定数)$$
2階微分が入っているので、一見、どうすればよいのか迷うかもしれません。
しかし、要するに2回微分すると0ですから・・1回だけの微分は『定数』」であるはず?? ・・という事に気付くと、解けます。1次関数 が解 というわけです。
対象の関数 微分公式 微分方程式の解法での役割 ①定数(定数関数) \({\large \frac{d}{dx}c=0}\) 微分すると0になる ②単項式「x の a 乗」 \({\large \frac{d}{dx}x^a=ax^{a-1}}\) 微分するとx の指数が1下がる
実際に、解となるはずである1次関数を「2回」微分してみましょう。
微分1回目:\(\frac{d}{dx}(bx+c)=b\)(定数)
微分2回目:\(\frac{d}{dx}b=0\)(ゼロ)→ OK
合わせると:\(\frac{d^2}{dx^2}(bx+c)=0\hspace{10pt}\rightarrow \frac{d^2}{dx^2}f(x)=0\hspace{5pt}の解\)
というわけで、確かに1次関数 bx + c は、2階微分=0という微分方程式の解です。
この解の導出過程では、「1階微分=(ゼロ以外の)定数」というタイプの微分方程式の解も、合わせて見つけている事になります。また、同じ論法を使うと、3階微分=0、4階微分=0といった微分方程式の解も同様に考える事が可能というわけです。
$$\frac{d^n}{dx^n}f(x)=0 の解は「(n-1)次関数」$$といった感じになるのです。
それでは次に、物理的には放物運動(2次関数のグラフの形)を表す微分方程式を見てみましょう。これについては高校の物理でも多分扱われていると思いますが、微分方程式の観点から考察してみましょう。
③ \(y^{\prime\prime}-b=0\)・・2次関数
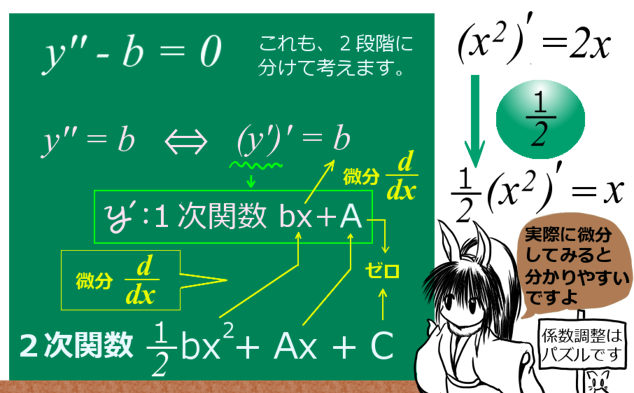
「2階微分が定数に等しい」という微分方程式です。(もちろん\(y^{\prime\prime}=b\)と書いても同じです。b = 0 の場合は2階微分=0のタイプですから、b≠0 と考えてください。)
■ 数学的な解法 ■ 物理的な意味・・地上での水平投射の重力による運動 (放物運動)
解法:1回微分すると1次関数→2回微分すると定数 と考えよう
「2階微分=もとの関数」という微分方程式
$$ \frac{d^2}{dx^2}f(x)-b=0$$
「『2回』微分すると定数になる」関数はなんだろう?という方程式です。
$$解: 2次関数\hspace{5pt}f(x)=\frac{b}{2}x^2+Ax+C\hspace{10pt}(A,C:定数、b は微分方程式内で使われてる係数)$$
この3つ目のタイプの微分方程式の場合、2回微分すると定数・・という事ですから、「1回微分すると1次関数」を見つければよいのです。
対象の関数 微分公式 微分方程式の解法での役割 ①定数(定数関数) \({\large \frac{d}{dx}c=0}\) 微分すると0になる ②単項式「x の a 乗」 \({\large \frac{d}{dx}x^a=ax^{a-1}}\) 微分するとx の指数が1下がる
単項式の微分公式を見ると、1回微分するごとに指数(xの「〇乗」の〇)が1下がりますから、2次関数を1回微分すると1次関数になりますね。
ですから、解となる関数は「2次関数」です。
実際に微分して確かめてみよう
実際に微分をしてみて、確かめてみましょう。
微分1回目:
微分2回目:
合わせると:
物理的には、運動方程式においては「地上で物を投げた時」の運動を表します。座標同士の関係を表す軌道が2次関数の関係式になるので、放物線を描きます。
物理的意味:地上での水平投射 重力だけが働く場合は放物運動
ここでは、運動方程式で働く力が「重力」であるとします。これは、地球上では物体の質量が定まれば一意的に決まり、その大きさは mg (≒9.8m) である事が知られています。この時、水平に物を投げる(「投射する」)と、軌道は2次関数のグラフである放物線になる事を見ましょう。
■ ①考え方・・水平方向と垂直方向に分ける ■ ②設定をして、2方向の2本の運動方程式を作ろう 運動方程式の解から軌道の関係式を作ると、2次関数つまり「放物線」が得られる
① 考え方・・水平方向と垂直方向に力の働き方を分ける
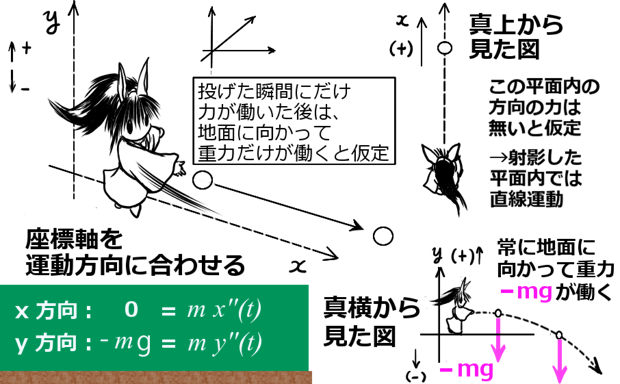
水平に物を投げる(投射する)運動を考えます。投げた瞬間には力が働いているかもしれませんが、一旦手などを離れたら、水平方向には力は働かず、地面に向かう方向にのみ重力が働くと考えて数式を組み合わせるのです。
地面に対して水平(平行)な向き:力は働かない
地面に対して垂直(直角)な向き:重力 mg [N] が地面に向かう向きで働く 上記の「2階微分=0」の微分方程式の物理的意味の項目で、平面や空間の運動で運動方程式を考える場合は、力を分解して「座標成分ごとに運動方程式を立てる」という事を述べました。ここでも、同じ考え方をします。
この場合は、3次元で考えてもよいのですが、最初に物を放り投げた方向に向かって上手に1つの座標軸を合わせたと考えると、すなわち平面で考えても全く同じ運動を表せます。
空気抵抗力などがなく、ひたすら地面に向かって同じ大きさの重力 -mg が働くと仮定します。こういうボールみたいなものを投げる時、力学的には、「『回転』もないものとする」という仮定も、一応重要です。 (※働く力が重力だけであると想定するので、「水平方向には力は働かない」=「水平方向だけで見れば等速直線運動」という事が保障されるので、そのように考えてよいわけです。「直線」という事については、地面の真上から見れば「直線」になっているという事です。このような見方を「射影(しゃえい)」と言います。)
② 設定をして、2方向の2本の運動方程式を作る
このようにして考える時、どちら向きがプラスでどちら向きがマイナスかも含めて、座標軸の向きの設定を行ってから運動方程式を立てます。今、運動は平面で考える事にして、座標軸は x 軸と y 軸であるとします。
座標軸の設定
x 軸:地面に対し水平方向、物体が投射される平面内、進行方向が+プラス
y軸:地面に対して垂直、地面から空の向きが+プラス、空から地面への向きが-マイナス
そして、2本の運動方程式を立てましょう。※尚、この場合に仮に3本目を立てたとしても、その向きには働く力はゼロ、位置もゼロから動かないので 0 = 0 という式ができるだけです。
x 軸成分:
\(0=m\frac{d^2x(t)}{dt^2}\) → 「2階微分=0」なので、解は t の1次関数ですね
y軸成分:\(-mg=m\frac{d^2y(t)}{dt^2}\hspace{5pt}\Leftrightarrow \hspace{5pt}-g=\frac{d^2y(t)}{dt^2}
\) → 「2階微分=定数」の微分方程式で、t の2次関数 というわけです。 y 軸成分の運動方程式で「力」の部分を – mg としているのは、空 → 地面方向は「マイナス」向きと設定したためです。地面方向に向かう「重力」の符号もマイナスにするのです。
② 運動方程式の解から軌道の関係式を作ると、2次関数つまり「放物線」が得られる
という事は、$$x(t)=bt+c,\hspace{5pt}y(t)=-\frac{g}{2}t^2+Bt+C $$という形の2式が、微分方程式である運動方程式の解として、出てくるわけです。
これで、軌道が確かに「放物線」である事が表現されたわけですが、座標軸の正負の向きの設定などから、上記の各定数について b > 0 、A > 0 となるので、最後の結果で \(-Ax^2\)(例えば \(– 2x^2\))という形が出てくるという事は、きちんと「下に落ちていく」という事も表しています。
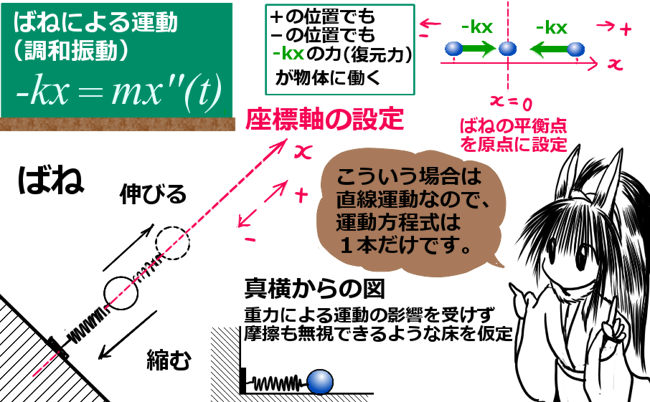
さて次は、三角関数が解になるタイプの微分方程式です。じつは、これは物理の力学で言うと「ばねの運動」なので、空間でも平面でもなく、「一次元(直線運動)」と考えてよいパターンです。ですから運動方程式は1つだけ作ればよいので、意外と考察しやすいかもしれません。
④ \(y^{\prime\prime}+b^2y=0\)・・調和振動(単振動)
このタイプの微分方程式は、2階微分と「元の関数」が入っていて、定数倍の関係にあるというものです。三角関数が関係し、物理的には抵抗力などが無い場合の「ばねの運動」(調和振動、単振動とも言います)を表します。
■
数学的解法 ■
物理的な意味:ばねの運動は三角関数(調和振動、単振動)
数学的解法:まず「2回微分すると元の関数の定数倍」になる関数は?
「2階微分=もとの関数の正の定数倍」という微分方程式
$$ \frac{d^2}{dx^2}f(x)+b^2f(x)=0$$
「『2回』微分すると『もとの関数の負の定数倍』になる」関数はなんだろう?という方程式です。
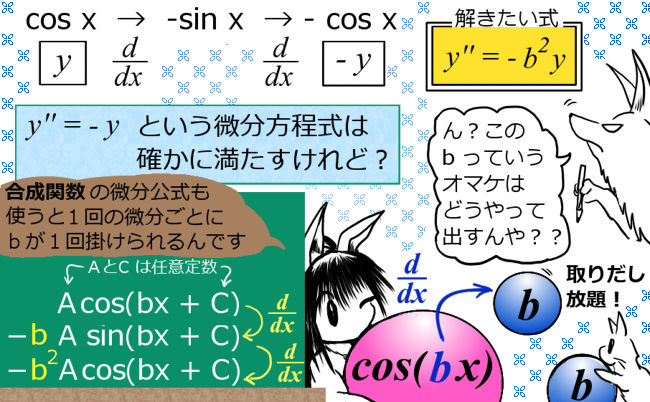
$$解: 三角関数\hspace{5pt}f(x)=A\cos (bx+C)\hspace{10pt}(A,C:定数、b は微分方程式内で使われてる係数)$$
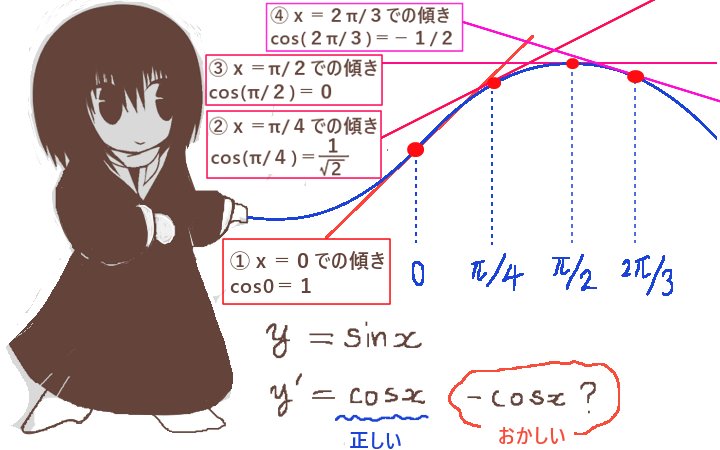
「2回微分するともとの関数の『マイナスの定数倍』」というものは、微分公式にあるでしょうか?三角関数は、これに似ています。実際、これをパーツとして使えるのです。この時、正弦でも余弦でも同じ事なので、ここでは余弦 cos x を、使います。
対象の関数 微分公式 微分方程式の解法での役割 ④-1 三角関数(正弦関数) \({\large \frac{d}{dx}\sin x=\cos x}\) 微分2回で元の関数の符号±入替 ④-2 三角関数(余弦関数) \({\large \frac{d}{dx}\cos x=-\sin x}\) 微分2回で元の関数の符号±入替 ⑤合成関数の微分 \({\large \frac{df(y)}{dx}=\frac{df(y)}{dy}\frac{dy(x)}{dx}}\) 微分方程式内の定数倍などを調整
三角関数を2回微分すると、もとの関数の「マイナス倍」になります。
そのためには、じつは合成関数の微分公式を考えればよいのです。この考え方は、このページで紹介するタイプ以外の微分方程式でも有効な手段です。
例えば cos(2x) の微分を1階と2階について見ますと、$$1階微分:\frac{d}{dx}\cos (2x)=(2x)^{\prime}(-\sin (2x))=-2\sin (2x)$$
$$2階微分:\frac{d^2}{dx^2}\cos (2x)=\frac{d}{dx}(-2\sin (2x))=-4\cos (2x)$$
になります。y = 2x , cos(2x) = cos y と考える事ができるので、合成関数の微分公式が適用できるのです。係数として「2」というのが掛けられていますが、それが合成関数の微分由来で出てくる係数というわけです。
・・すると、この cos (2x) という関数は、2回微分するともとの関数 cos (2x) の – 4 倍になっているので、 「2回微分するともとの関数の『マイナスの定数倍』」 の条件を満たす関数の仲間である事が分かります。
という事は、定数倍として\(-b^2\)がほしいのであれば、
任意定数については、まず A を任意定数として、A cos(bx) という形でも解として成立するのです。また、別の任意定数 C を用いて Acos(bx+C) という形でも、じつはOKなのです。これは、合成関数の微分を行う時に、bx + C を x で微分すると b は生き残りますが C はゼロになって消えるためです。
実際に微分して確かめてみよう!
つまり、総合すると Acos (bx+C) という関数が、解になるという事です。正弦で考えても同様の形になります。実際に微分してみて、確かめてみましょう。
微分1回目:\(\frac{d}{dx}A\cos (bx+C)=-bA\sin(bx+C)\)(マイナスの正弦)
微分2回目:\(\frac{d}{dx}\{-bA\sin(bx+C)\}=-b^2A\cos (bx+C)\)
合わせると:
物理的には、運動方程式を考えると、このタイプの微分方程式は「ばねの運動」を表します。ばねというと、いかにも人工的な響きがありますが、別に工学だけで用いるというものでもありません。例えば、ミクロの領域での分子の振動などを、ばねと同じタイプの振動(調和振動)と考えるモデルをもとにして考察する事が、量子力学や量子化学でもなされるのです。
物理的意味:ばねの運動は三角関数(調和振動、単振動)
運動方程式で、ばねにつながれた物体の運動を考えると、上記の「2階微分=負の定数×もとの関数」という微分方程式になります。ばねは、抵抗力が働かないなら伸びたり縮んだりを繰り返しますから、周期関数である三角関数が解であるという事はその事実と調和しているというわけです。
■ ①
まずは設定をしよう ・・一次元の運動として扱えます ■ ②
解いてみて完成 ・・結果は三角関数です
① まずは設定をしよう
抵抗力がない状態で、ばねの伸び縮みの力だけで、ばねにつながれた物体が(振動)運動しているとします。この場合は、1次元の直線運動と考えてよいので、運動方程式を3つ・2つ立てる必要はなく、1つでよいのです。ですから、式さえ立てれば、結構分かりやすいと思います。
ばねの力の大きさは、ばねの「伸び」または「縮み」に比例します。(「フックの法則」と言います。)
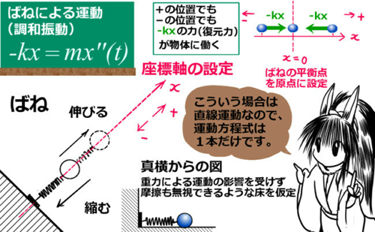
ただ、プラスマイナスの符号にだけは注意しましょう。まず、ばね定数 k は正の値であるとします。次にばねの平衡点を原点 x = 0 として、座標の正負の向きを次のように設定します。
原点から見て、ばねが伸びている方向:プラス方向
原点から見て、ばねが伸びている方向:マイナス方向
この時、ばねによる力の向きを考えてみます。符号に注意してください。
ばねが伸びている時・・つまり位置座標が正の値の時:
ばねが縮んでいる時・・つまり位置座標が負の値の時:
これをまとめますと、「ばねの力は位置座標と常に逆の符号」という事です。
$$ばねの力:F = -kx(t)\hspace{10pt}(x(t):位置座標、ばね定数 k>0)$$
そうしますと運動方程式は次のようになるわけです。
$$-kx(t)=m\frac{d^2x(t)}{dt^2}\hspace{10pt}\Leftrightarrow \hspace{10pt}\frac{d^2x(t)}{dt^2}+\frac{k}{m}x(t)=0$$
物体の運動の様子を調べるにはこれを解けばよいわけですが、もう分かっているわけです!
② 解いてみて完成
ばねにつながれた物体に関する運動方程式\(\frac{d^2x(t)}{dt^2}+\frac{k}{m}x(t)=0\) は、
もう少し物理的に見通しをよくするために、
このオメガ \(\omega\) という記号は、ばねの調和振動に限らず、回転運動などの周期的な運動における角速度 、角振動数 、角周波数 (1秒間に何ラジアン回るか)を表します。ばねの場合は「振動」ですので、角振動数と言う場合が多いです。いずれにしても、ばねの運動を周期運動と見た場合に、角度の部分(「位相」)がどのように変化するかを表す値というわけです。
ここでは \(\frac{k}{m}=\omega^2\) と、おいただけでしたから、そのような角振動数は、物体の質量とばねの性質(ばね定数の大きさの違い)によって決まるという事も分かります。
さて、使用する実質5つの公式のうち、まだ使っていないのが 自然対数の底 e の指数関数の微分公式です。最後に紹介するタイプの微分方程式は、この e の指数関数の微分公式を用いて解けます。
⑤ \(y^{\prime\prime}+by^{\prime}+x=0\)・・粘性抵抗ありのばねの運動
5つ目の微分方程式として、\(y^{\prime\prime}+by^{\prime}+x=0\) で「『特性方程式』が異なる2つの実数解を持つ場合」 を説明いたします。この、後のほうにくっついてる妙な条件は別になくてもきちんと微分方程式は解けるのですが(特性方程式を使った一般の場合の解法 )、簡単なのがこの条件の場合ですので、この場合を述べます。
■
数学的解法 ■
物理的意味:粘性抵抗が「強い」場合のばねの挙動
数学的解法:e の指数関数の微分を使おう
これの説明は他のものと比べて少し長いですが、「公式を上手に当てはめれば解ける」という事には変わりありません。
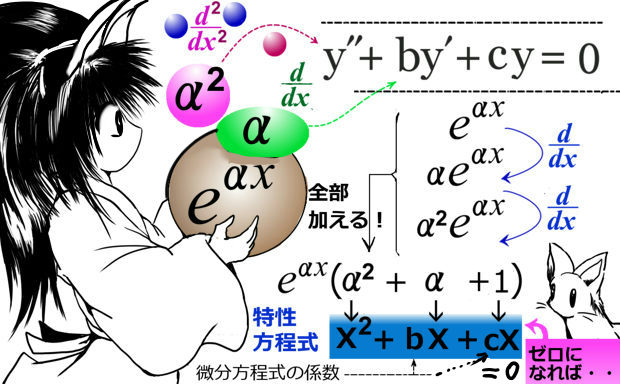
\(y^{\prime\prime}+by^{\prime}+cy=0\)という形の微分方程式
$$ \frac{d^2}{dx^2}f(x)+b\frac{d}{dx}f(x)+cf(x)=0\hspace{10pt}x^2+bx+c=0が異なる「2つの『実数解』」を持つ場合$$
このような形の方程式で、何やら変な条件がくっついている場合の微分方程式です。
$$解: e の指数関数\hspace{5pt}f(x)=Ae^{\alpha x}+Be^{\beta x}$$
$$(A,B:定数、\alpha, \beta は x^2+bx+c=0 の解(異なる2つの実数解)$$
このタイプの微分方程式を解くには、e の指数関数の性質と、1つ前の微分方程式の例でも用いた
対象の関数 微分公式 微分方程式の解法での役割 ③自然対数の底 e の指数関数 \({\large \frac{d}{dx}e^x=e^x}\) 微分すると元の関数に戻る ⑤合成関数の微分 \({\large \frac{df(y)}{dx}=\frac{df(y)}{dy}\frac{dy(x)}{dx}}\) 微分方程式内の定数倍などを調整
考え方を簡単に述べましょう。三角関数で cos (bx) 等を考えた時は、
この \(e^{\alpha x}\) という関数を微分すると、
微分してないもとの関数:\(e^{\alpha x}\)
微分1回目:\(\frac{d}{dx}e^{\alpha x}=\alpha e^{\alpha x}\)
微分2回目:\(\frac{d^2}{dx^2}e^{\alpha x}=\alpha^2 e^{\alpha x}\)
ポイントは、「これらを加え合わせてみる 」という事です。
では今度は、定数倍も考えて、
\(\alpha\) が \(\alpha^2+b\alpha +c=0\) となる事を、
全く同じ意味で、次のようにも言い換えられます。
$$「\alpha が x^2+bx +c=0 の解である」$$
そしてそのような場合、じつはまさしく上の微分方程式の形:
POINT
$$\alpha が x^2+bx +c=0 の解である時、e^{\alpha x}は$$
$$\frac{d^2}{dx^2}f(x)+b\frac{d}{dx}f(x)+cf(x)=0の解の1つ$$
また、任意定数を A として、\(Ae^{\alpha x}\) も解になります。
さて、\(\alpha が x^2+bx +c=0\) の「実数解」である時で、重解では無い時 、
解:「特性方程式」が2つの異なる実数解を持つ場合
$$\alpha と\betaを x^2+bx +c=0 の異なる2つの解、A と B を任意定数として、$$
$$\frac{d^2}{dx^2}f(x)+b\frac{d}{dx}f(x)+cf(x)=0の解は$$
$$Ae^{\alpha x}+Be^{\beta x} で表されます。$$
■ 特性方程式が重解を持つ場合と、実数解をもたない場合にも微分方程式を解く事はできますが、これは別の記事で詳しく述べましょう。指数関数の微分の性質が重要である点は同じです。
物理でも、運動方程式がこのタイプの微分方程式になる事があります。それについて、見てみましょう。
物理的意味:粘性抵抗が「強い」場合のばねの挙動
ばねにつながれた物体の運動を表す運動方程式には、位置座標(1次元・直線)の「2階微分」と、「もとの関数の定数(ばね定数)倍」という項が含まれています。粘性のある流体の中のばねの運動の場合、これに粘性抵抗力 が加わり、
■ 設定をして運動方程式を解く ■ どういう運動かを考察してみよう
設定をして運動方程式を解く
まず、座標の設定としては、抵抗力のないばね運動の時と同じで、一次元の運動と考えてよいのです。ばねの平衡点を原点として、伸びる方向をプラス方向、縮む方向をマイナスとします。
次に、力を整理しましょう。ばねの力と、粘性抵抗力の2つがあります。粘性抵抗力は、運動を妨げる方向に働きますので、マイナス符号をつけるのです。(この抵抗力の符号の考え方は、空気抵抗力や摩擦力に対しても同じです。)
この場合に働く2つの力
ばねの力:\(-kx\) k:ばね定数(正の値)
粘性抵抗力:\(-\rho \frac{dx(t)}{dt}\) \(\rho\):てきとうな比例定数(正の値)
すると、運動方程式は次のようになります。 $$-kx-\rho \frac{dx(t)}{dt}=m\frac{d^2x(t)}{dt^2}$$ $$\Leftrightarrow \frac{d^2x(t)}{dt^2}+\frac{\rho}{m} \frac{dx(t)}{dt}+\frac{k}{m}x=0$$ $$\left(\Leftrightarrow \frac{d^2x(t)}{dt^2}+2\gamma \frac{dx(t)}{dt}+\omega^2x=0\hspace{10pt}\gamma=\frac{\rho}{2m},\omega^2=\frac{k}{m}\right)$$ 最後の形には別に変形しなくてもよいのですが、この形だと、解を出しやすいです。
特性方程式が「異なる2つの実数解を持つ」という条件が満たされているとすると、上記の要領で解く事ができます。一応、特性方程式の解を出しておきましょう。(※2次方程式なので比較的容易に出せる事に注意してください。)
$$特性方程式:X^2+2\gamma X+\omega^2X=0\Leftrightarrow (X+\gamma)^2-\gamma^2+\omega^2=0 $$
$$\Leftrightarrow (X+\gamma)^2=\gamma^2-\omega^2\Leftrightarrow X+\gamma=\pm \sqrt{\gamma^2-\omega^2}$$
$$\Leftrightarrow X=-\gamma \pm \sqrt{\gamma^2-\omega^2}$$
この2解(実数解という条件とします)を用いて、
どういう運動かを考察してみよう
解が出ましたので「これで終わり」でもよいのですが、少し汚い形という事もあって、結局どういう運動になるのかが分かりにくいですね。そこで、もう少しだけ考察をしてみましょう。
特性方程式の2解の形をよく見ますと、
\(X=-\gamma \pm \sqrt{\gamma^2-\omega^2}\) は、これが実数解であるという前提で、
という事は、特性方程式の2解を、「正の定数」\(p,\hspace{5pt}q\hspace{5pt}を用いて X=-p,-q\)と書くと、
微分方程式のほうの解は、
$$x(t)=Ae^{-pt}+Be^{-qt}$$
となります。これだと多少見やすくて、p と q を正の数だとしましたから、これらにマイナスがついたものが指数に来ているという事は、時間に関して「単調減少」の関数であり、しかも変数の値が大きくなるとゼロに近づいていく事が分かります。
また、普通の指数関数ですので、三角関数と違って「振動」もしません。
この考察をまとめると、例えば次のような事が言えるのです。
粘性抵抗が強い場合の考察
時間が経てば経つほど,位置座標の x(t) の値は小さくなり、
位置座標 x(t) は通常の指数関数で表されているので、振動はしない。
特性方程式が2次方程式の場合、実数解を持つかは \(\sqrt{\gamma^2-\omega^2}\) の中身が正か負かで決まるわけですが、
微積分学や物理の入門としては、まず「高校で教わった事を直接使える」ものについて、いくつか具体例を見ながら中に入っていけた事になります。同じように、まずは手持ちの知識を用いて入っていける部分から、少しずつ新規の知識も知っていくようにすると大学数学の内容に無理なく入っていけると思います。