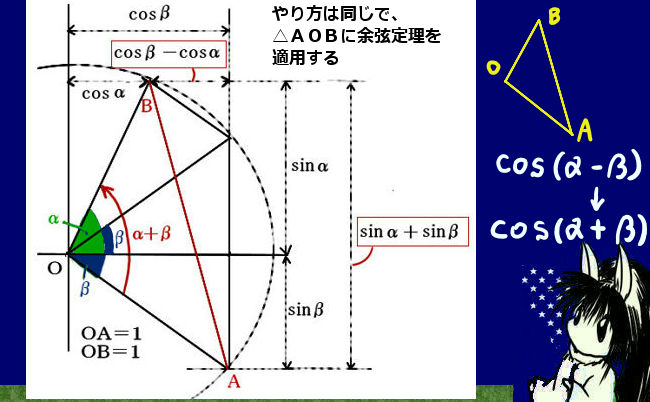
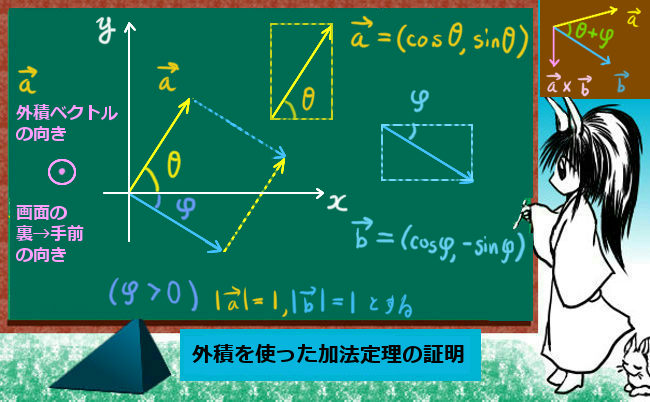
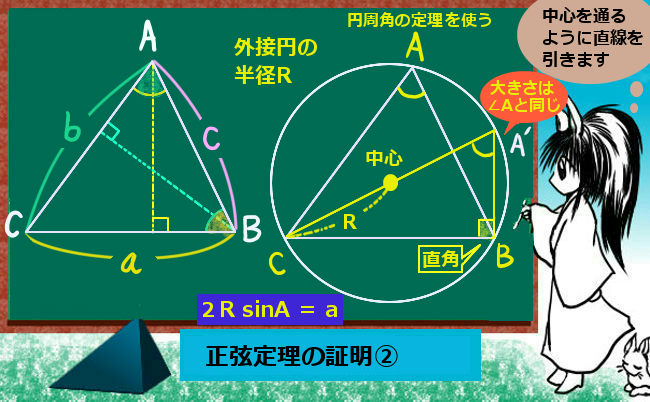
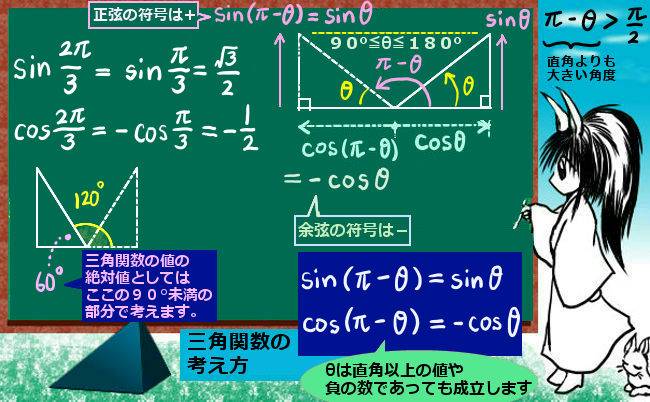
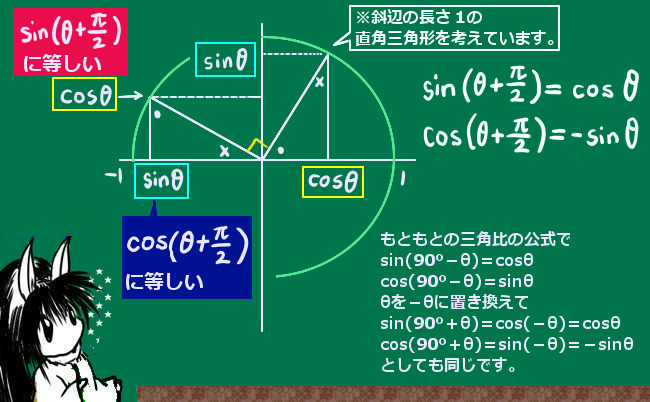
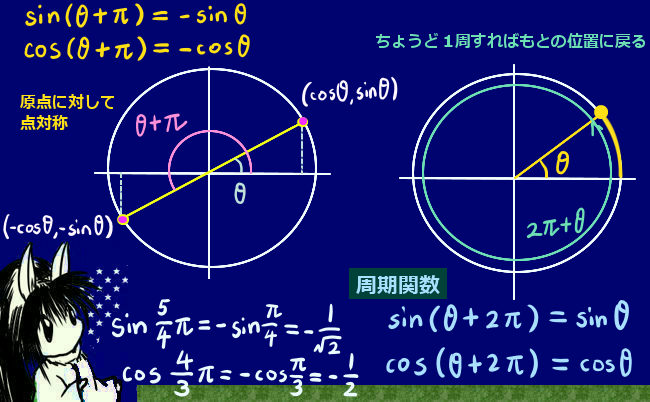
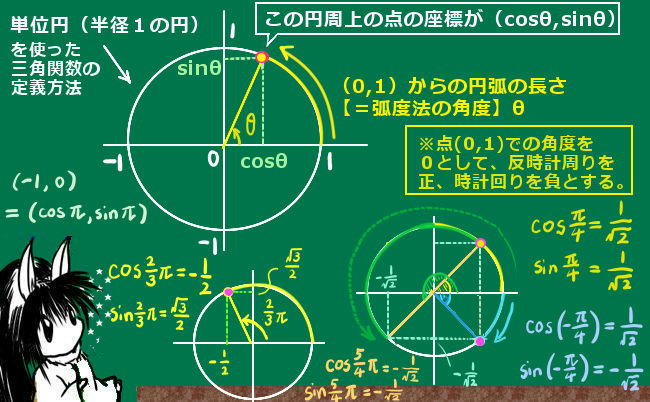
三角関数の積和の公式、和積の公式、倍角の公式、半角の公式という一連の公式は互いに本質的に異なるものではなく、全て三角関数の加法定理から導出されるものです。
(英:倍角の公式 double-angle formula 半角の公式 half-angle formula)
(和積の公式と積和の公式は、英語では加法定理の一部だと捉えられる事も多いようです。)
★高校数学の中の位置付けだと、まずこれらの公式よりも大事なのは加法定理であると言えます。これらの公式は、じつは加法定理さえ覚えていれはその場で割と簡単に導出が可能であるからです。
これらの和積の公式等を暗記するにしても、まずは加法定理との形との対応から慣れていき、入試問題などを解いて練習しながら覚えていくのがよいと思います。
公式の内容
積和の公式、和積の公式、倍角の公式、半角の公式の内容を順に記すと次のようになります。これらは切り離された別々の公式ではなくて、本質的には加法定理を目的に応じて使いやすいように変形したものです。
次の正弦と余弦の「積」に関する4式を言います。【三角関数の積の形を和にする公式です。】$$\sin A \cos B=\frac{\sin (A+B)+\sin (A-B)}{2}$$ $$\cos A \sin B=\frac{\sin (A+B)-\sin (A-B)}{2}$$ $$\cos A \cos B =\frac{\cos (A+B)+\cos (A-B)}{2}$$ $$\sin A \sin B =-\frac{\cos (A+B)-\cos (A-B)}{2}$$
次の正弦と余弦に関する4式を言います。【三角関数の和や差の形を積にする公式です。】$$\sin C +\sin D =2\sin\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)$$ $$\sin C -\sin D =2\cos\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)$$ $$\cos C +\cos D =2\cos\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)$$ $$\cos C -\cos D =-2\sin\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)$$ 後述しますが、ここで使っているCやDは、加法定理や上記の積和の公式でのAとBを使ってC=A+B, D=A-Bとおいたものです。
正弦と余弦に関する倍角の公式は次の2式です。
$$\sin 2A=2\sin A\cos A$$
$$\cos 2A=\cos ^2A-\sin ^2A$$
余弦のほうはcos2A=2cos2A-1=1-2sin2Aとも表せます。
正接の倍角の公式は tan2A=(sin2A)/(cos2A)で計算します。
正弦と余弦に関する半角の公式は次の2式です。
$$\cos A=\pm\sqrt{\frac{1+\cos 2A}{2}}$$
$$\sin A=\pm\sqrt{\frac{1-\cos 2A}{2}}$$
プラスマイナスの符号は角度に応じて適切なほうを選びます。
A=X/2といった置き換えをすると「半角」という事をより明確にもできます。
正接の半角の公式も正弦を余弦で割って計算できます。
ところで、これらの式の数を合計すると12個ありますね。これらを1つ1つ、別々の公式として暗記するのは大変です。そのため、もとになっている加法定理を変形したものであるという見方のほうが勧められます。
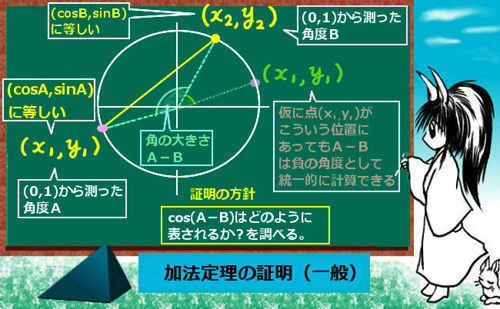
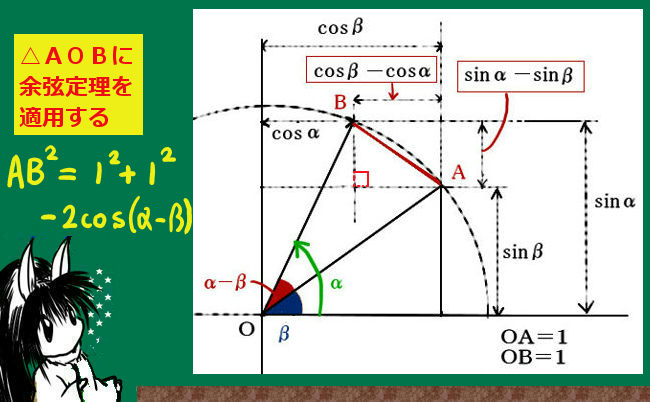
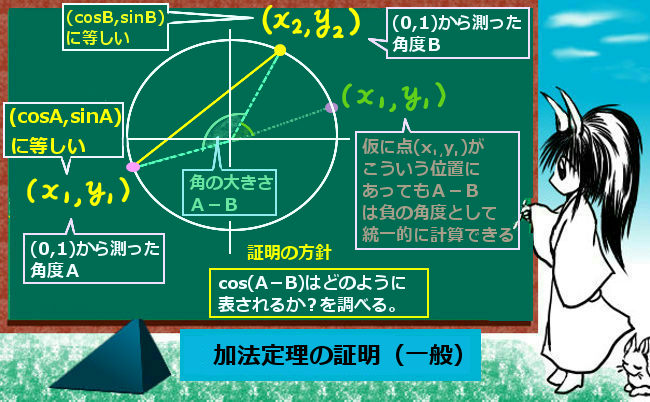
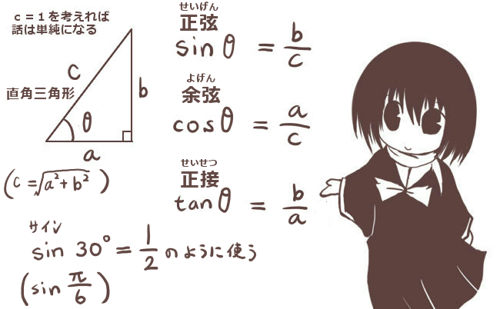
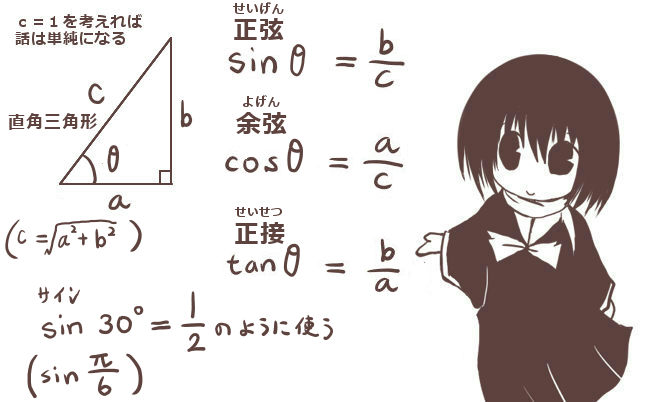
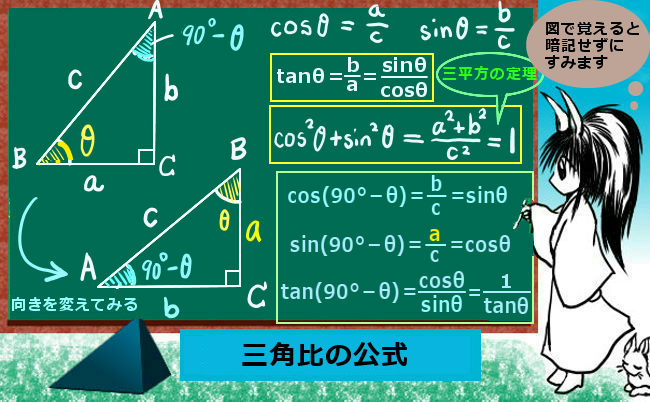
三角関数の加法定理については証明も含めて別途に詳しく述べていますが、正弦と余弦について結果だけ記すと次のようになります。
- sin(A+B)=sinAcosB+cosAsinB
- sin(A-B)=sinAcosB-cosAsinB
- cos(A+B)=cosAcosB-sinAsinB
- cos(A-B)=cosAcosB+sinAsinB
これらを組み合わせると和積・積和の公式が導出され、角度の1つを置き換えると倍角の公式になります。
半角の公式については倍角の公式を変形して導出する事になります。
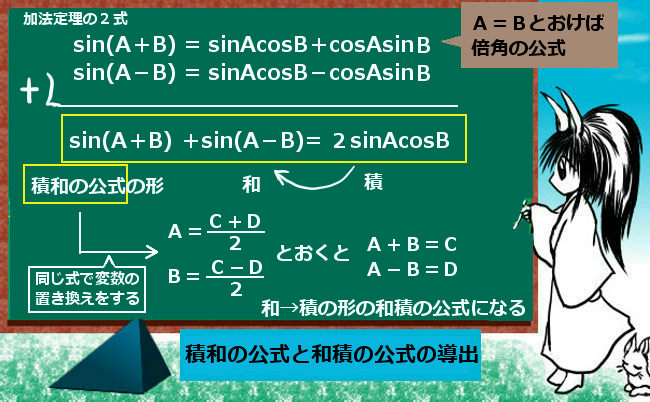
証明①:積和の公式
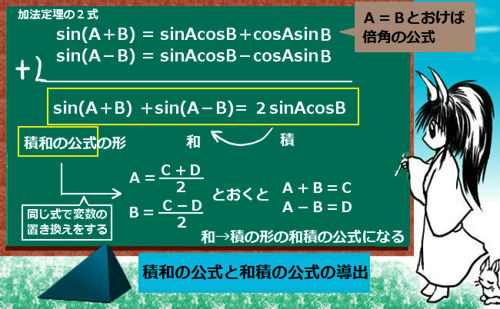
加法定理の4式のうち、正弦同士、余弦同士を見ると、2つの項は符号が違うだけで同じ形をしています。この事を使います。
まず、正弦についての加法定理の2式を加えてみましょう。
sin(A+B)+sin(A-B)=sinAcosB+cosAsinB+sinAcosB-cosAsinB=2sinAcosB
本質的にはこれだけでよくて、和積の公式も積和の公式も、本質的には本来はこの同じ形の関係式です。ただ、三角関数の積を和に直すか、和を積に直すかで少しだけ形を変えて「公式」としているだけです。まず、積和の公式は上記の式の両辺を単純に2で割って、積が和の形になるようにします。
$$\sin A \cos B=\frac{\sin (A+B)+\sin (A-B)}{2}$$
他の3式も、加法定理の2式を加える・2式の差をとる事で導出します。
$$\sin (A+B)-\sin (A-B)=2\cos A \sin B\Leftrightarrow\cos A \sin B=\frac{\sin (A+B)-\sin (A-B)}{2}$$
$$\cos (A+B)+\cos (A-B)=2\cos A \cos B\Leftrightarrow\cos A \cos B =\frac{\cos (A+B)+\cos (A-B)}{2}$$
$$\cos (A+B)-\cos (A-B)=-2\sin A \sin B\Leftrightarrow\sin A \sin B =-\frac{\cos (A+B)-\cos (A-B)}{2}$$
証明②:和積の公式
では、和の形を積に直している和積の公式は、どのように出すのでしょう。
じつは使う式は全く同じで「変数の置き換え」をするのです。
一般的には次のようにします。
まずA+B=C,A-B=Dのようにおき直します。
次にこの2式を加えると 2A=C+D ⇔ A=(C+D)/2
片方からもう片方を引くと2B=C-D ⇔ (C-D)/2
このようになる事を使って、式を整理して公式としています。
$$\sin (A+B)+\sin (A-B)=2\sin A \cos B においてA=\frac{C+D}{2}, \hspace{5pt}B=\frac{C-D}{2}とおくと$$
$$\sin C +\sin D =2\sin\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)$$
加法定理の2式の和ではなく「差」をとると、正弦の差を積に直す形の公式が得られます。
$$\sin (A+B)-\sin (A-B)=2\cos A \sin B においてA=\frac{C+D}{2}, \hspace{5pt}B=\frac{C-D}{2}を代入します。$$
$$\sin C -\sin D =2\cos\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)$$
余弦のほうについても、加法定理の2式を加える・差をとる事で公式を導出します。まず余弦に関する和積の公式の和の形のほうのものは次のようになります。
$$\cos (A+B)+\cos (A-B)=2\cos A \cos B においてA=\frac{C+D}{2}, \hspace{5pt}B=\frac{C-D}{2}を代入します。$$
$$\cos C +\cos D =2\cos\left(\frac{C+D}{2}\right)\cos\left(\frac{C-D}{2}\right)$$
差の形のほうは次のようになります。
$$\cos (A+B)-\cos (A-B)=2\cos A \cos B においてA=\frac{C+D}{2}, \hspace{5pt}B=\frac{C-D}{2}を代入します。$$
$$\cos C -\cos D =-2\sin\left(\frac{C+D}{2}\right)\sin\left(\frac{C-D}{2}\right)$$
具体例:
例えば、唐突に sin75°+sin15°の値はいくらかと聞かれたらこの公式を使えば即座に答えは出るという事です。(こういう問いは理解度を試すための問題で、高校数学以外ではあまりやりません。)
(75°+15°)÷2=45° と (75°-15°)÷2=30° の正弦の値を使います。$$\sin 75°+\sin 15°=2(\sin 45°)(\cos 30°)=2\cdot \frac{\sqrt{2}}{2}\cdot\frac{\sqrt{3}}{2}=\frac{\sqrt{6}}{2}$$
加法定理で75°=30°+45°などとして加法定理を使って計算しても結果は同じです。ただ、和積の公式を知っていると多少計算は速く済みます。
証明③:倍角と半角の公式
次に倍角の公式と半角の公式と呼ばれる式の導出方法です。
これらもまた別々のものではなく、本質的には同じ式であるものを変形したものです。

まずは倍角の公式から見ましょう。
sin2A=2sinAcosA という式ですが、
じつはこれは、加法定理で2つの角度についてA=Bとしているだけなのです。
余弦のほうの倍角の公式も、やり方は同じです。
つまり次のようにします。
sin(A+B)=sinAcosB+cosAsinB において A=Bとして sin2A=2sinAcosA
cos(A+B)=cosAcosB-sinAsinB において A=Bとして cos2A=cos2A-sin2A
余弦のほうは、cos2A+sin2A=1を使ってcos2A=2cos2A-1、もしくはcos2A=1-2sin2Aとも表せます。
次に半角の公式の導出です。
このページで紹介している公式のうち半角の公式についてだけは加法定理から直ちには出せず、余弦のほうの倍角の公式を変形する事になります。
(ただし倍角の公式が簡単に出るので、導出に手間はかからないはずです。)
cos2A=2cos2A-1 ⇔ cos2A=(cos2A+1)/2 から余弦の半角の公式、
cos2A=1-2sin2A ⇔ sin2A=(cos2A-1)/2 から正弦の半角の公式を得ます。
2乗がありますので、平方根を考える事になります。
$$\cos A=\pm\sqrt{\frac{1+\cos 2A}{2}}$$
$$\sin A=\pm\sqrt{\frac{1-\cos 2A}{2}}$$
平方根をとる時に一般の場合では符号が確定しませんが、具体的に例えばプラスの鋭角に対する「半分の角度」を考えるのであれば、余弦も正弦もプラスのはずなので、プラス符号のほうをとります。
このように倍角・半角の公式もまた、基本は本質的に加法定理によるものであるわけです。加法定理さえ覚えておけば、例えば倍角の公式は暗記しなくても即座に出てきますし、半角の公式で正弦・余弦の公式がともに余弦を使って表される事も理解できて覚えやすいはずなのです。
尚、角度Aに対する3倍の3Aを考えた3倍角の公式、4倍角の公式、・・なども一応存在します。
ただしこれらも同様に、いずれも加法定理から出せる関係式ですので一般的には暗記しなくてもよい場合も多いと思われる事項です。
参考までに、複素数に関するド・モアブルの定理を使うと、そういった三角関数の3倍角の公式などの形を比較的容易に知る事も可能です。
積和の公式や倍角の公式などは、大学入試で直接計算を問われる場合以外には、三角関数に関する積分の計算に使う事が比較的多いように思います。例えば、sinxcosxの原始関数(微分すると対象の関数となる関数)は微分の公式だけからは即座には分かりにくいので、倍角の公式を思い出してこれを (sin 2x)/2の形にして積分の計算をするといったものです。
また、物理学で2つの正弦波の重ね合わせをするときも、和積の公式を知っていると即座に結果を計算できるので便利です。
この手の三角関数の微積分での変形計算は大学入試でも問われるかもしれませんが、大学数学の微積分の一部でも重要である場合があります。ただし繰り返しになりますが、加法定理とこれらの公式の導出の方法の大筋さえ覚えておけば、もし公式を忘れてしまってもすぐにその場で計算できるようになります。