矢印で表される「ベクトル」と通常の数(スカラー)との違いについて説明します。
■関連サイト内記事(ベクトルに関する記事)
■物理学へのベクトルの応用
これらの他にも、力学・電磁気学等でベクトルによる考え方は多く使えます。
べクトルの考え方とイメージ
基本的には、ベクトルとは「方向」と「大きさ」の2つの合わせ持つ量として考えられます。通常の正の実数や自然数などは「大きさ」しか持ちません。
◆プラスとマイナスを「互いに逆の方向」とみなせば通常の実数等も「互いに逆向きの2つの方向」を持っているとも言えますが、ベクトルは平面や空間のあらゆる向きの方向を考えます。
イメージとしては、平面上の線分が向きを持っているという感じです。
(空間内の線分でも同じです。平面上のベクトルを特に平面ベクトル、空間内のベクトルを特に空間ベクトルと呼ぶ事もあります。数学的には、より「次元の高い」ベクトルも定義できます。)
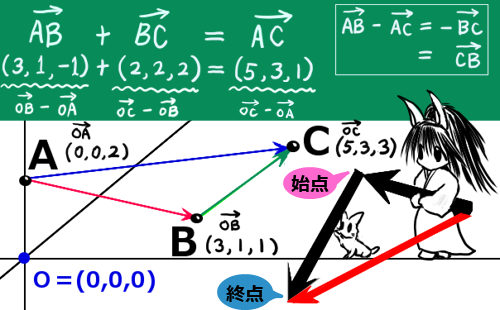
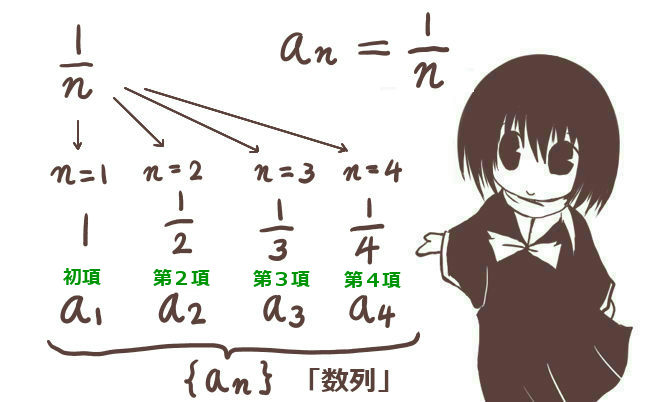
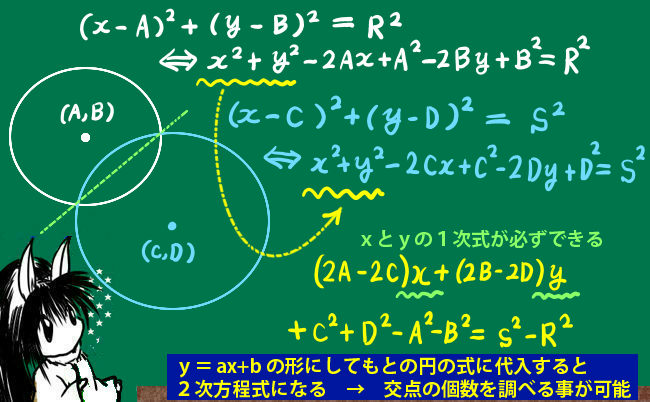
平面に点Aと点Bを結ぶ線分があった時、その線分は長さ(大きさ)を持ちます。その線分に対して、「AからBに向かうのか」「BからAに向かうのか」という事も決めたものが「ベクトル」であるというのが基本的なイメージです。
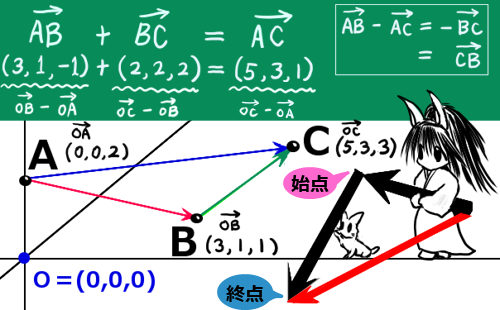
この図では空間ベクトルの色々な表記法・計算などを図示しています。
ベクトルの矢印の始まりの点を「始点」、矢印の先端の点を「終点」と言います。ベクトルは、座標の成分でも表す事ができます。数学的には、座標成分で表す方法のほうが色々な計算で便利です。ただし、物理でベクトルを用いる場合は、図形的な考察も重要となる場合があります。
この考え方は、例えば力学の「速度ベクトル」で使います。
例えば点Aから点Bの間で物体が移動しているという時に、
「AからBに向かっているのか」「BからAに向かっているのか」で、運動の性質は当然異なります。
それを数式としてはベクトルで表現するのです。
◆より詳細に言うと、
ベクトルとは「向きと大きさを持ち、加算、減算、定数倍、内積といった演算が定義できる」ものである事も重要です。それらの演算もまた、物理学等への応用でも使います。
動画声優担当ステ♪様 http://sute.tabigeinin.com/
BGM:音楽の卵
ベクトルの表記方法
ベクトルの表記方法はいくつかあります。
図形的に矢印で図示する方法、平面上または空間内の点を使って表す方法、原点を基準にした座標で表現する方法、などがあります。
①図形的に矢印で図示する方法
(始点と終点を明記する方法)
ベクトルは図形的に図示して表現する事ができます。この場合には、方向を持つ事を明確にするために、ただの線では無く「矢印」を用いるのが通例です。
この時には、向きが例えば「点Aから点B」の場合には矢印の先(矢の部分)を点Bの部分に書きます。
逆に、「点Bから点A」の向きであれば、
大きさは同じで逆向きのベクトルという意味で矢印の先を点Aに書くわけです。
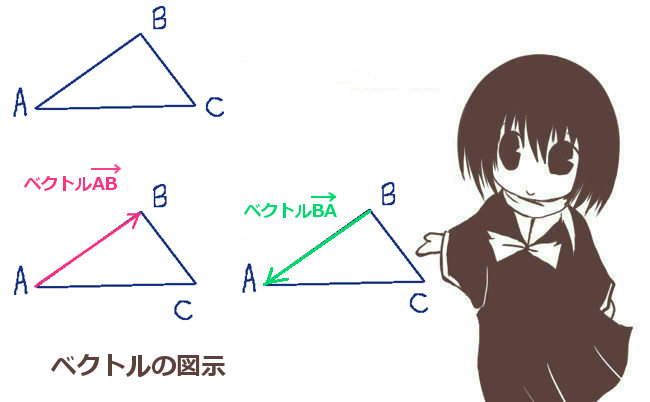
「点Xから点Y」に向かうベクトルがある時(この時に大きさも確定していますが)、
点Xをベクトルの始点、点Yをベクトルの終点と言う場合があります。
平面上だけでなく、空間内でも考える事ができます。
②平面上または空間内の点を使って表す方法
平面上または空間内において、原点Oから点Aへの向きと大きさを持つベクトルを、$$\overrightarrow{OA}$$と書く表記方法があります。
線分OA の上に「矢印」をつけるわけです。
点Oから点Aに向かう「方向付きの線分」ですよ、という意味合いです。
また、原点を基準とする事が明らかである場合は、次のようにも書きます。 $$\overrightarrow{a}$$
この場合には、点Pや点Qといった点の名称を使うよりは、何か適当な小文字(a, b, p, q, x, y, ・・・)を使う事が比較的多いように思います。
普通は \(\overrightarrow{OA}に対して\overrightarrow{a}、\overrightarrow{OB}に対して\overrightarrow{b}\) のようにアルファベットを対応させますが、これはあくまで分かり易くするためです。
「このベクトルをこの文字で表す」と明示しておけば、対応させなくても間違いではありません。
原点を基準としないベクトルも考える事ができます。
例えば、点Aから点Bに向かうベクトルは\(\overrightarrow{AB}\)と書くことができ、
逆に、点Bから点Aに向かうベクトルは\(\overrightarrow{BA}\)と書くことができます。
◆ベクトルに定数倍(スカラー倍)、加算、減算などの演算を定義すると、$$\overrightarrow{AB} =-\overrightarrow{BA}$$ という関係式が必ず成立します。(※厳密には、演算の定義が無いとマイナスの符号をつけるといった事自体に数学的な意味が発生しない事には注意。)この関係は、次に見る座標によるベクトルの表現を見る事でもイメージしやすくなります。
③座標を使った表記方法
直交座標上の原点(0, 0)を基準とする事を前提に、ベクトルを座標で表す方法があります。
この場合、「原点から特定の点まで」という「大きさ」と「方向」を定めているわけです。
例えば(1, 1)という座標は平面の直交座標において
「斜め右上45°方向の大きさ \(\sqrt{2}\) 」というベクトルを表す事ができるのです。
このようにベクトルを座標で表したとき、通常の座標のようにx成分、y成分といった言葉を使います。「あるベクトルのx成分、y成分はともに1」といった具合です。

この方法でベクトルを考えると、(1,1) というベクトルと( -1, -1) というベクトルは、大きさは同じで向きは逆向きである事がわかります。(図示でも、計算でも示せます。)
一般的に(x,y) と(-x,-y)という2つのベクトルは
「同じ大きさで逆向き」のベクトルです。
【例外は図形的な意味では向きが無いゼロベクトル (0,0)】
「逆向き」である事を、ベクトルにおいてもマイナス符号で表現します。
例えば\(\overrightarrow{A}=(x,y)\) であるなら、\(-\overrightarrow{A}=(-x,-y)\) です。
これは、1つのベクトルに対して
-1というスカラーを乗じたと考えても同じ事です。
【この計算はゼロベクトル (0,0)に対しても統一的に行う事ができます。】
なお、ベクトルの大きさを計算する方法は座標上の2点間距離を計算する方法と同じであり、三平方の定理を使います。
ベクトルを、始点と終点を明記して矢印で表す表記と、原点を基準にして座標で表す表記は、実は原則としては「向き」と「大きさ」を表現する方法としては同一視できるものです。ただし、ベクトルをどういうものとして考えるかの前提が必要にもなります。
■参考サイト内記事:ベクトルの相等:自由ベクトルと束縛ベクトル
④ボールド体表記(主に書籍等で使用)
通常の文字 a, b, x 等に対して、それらを「ボールド体」a, b, x 表記にする事でベクトルを表す場合もあります。
この表記は書籍では多用されますが、慣れてないと通常のスカラー変数なのかベクトルなのか、紛らわしいかもしれません。
ウェブ上だとさらに分かりにくい事があるので、
当サイトでは敢えてベクトルは全て「矢印」の表記にしています。
- 矢印表記:\(\overrightarrow{a} \)
- ボールド体表記 a・・これでベクトルを表す (通常の表記 a )
ボールド体表記は、当サイトではベクトルの表記としては使用しません。
スカラーとは?ベクトルとの違い
ある量がベクトルであるか通常の数であるのか区別が必要な時には、
ベクトルに対して通常の数(実数など)をスカラーと呼びます。
(※言葉としては「ベクトル量」「スカラー量」といった言い方もします。それぞれ、「ベクトル」「スカラー」と同じです。)
また、対象が関数である場合にはベクトル関数、スカラー関数と呼んで区別もします。変数、定数といった語にも同様にベクトル・スカラーの名称をつけて呼ぶ事があります。
| \(F(x), x, a\) | スカラー関数 スカラー変数 スカラー定数 |
| \(\overrightarrow{F}(x),\overrightarrow{x},\overrightarrow{a}\) | ベクトル関数 ベクトル変数 ベクトル定数(定ベクトル) |
「成分として」持つものを特に「ベクトル場」と呼ぶ事もあります。
ベクトル変数については、例えばスカラー関数をf\((\overrightarrow{x})\) のように表す事もあります。これはx,y,zの座標によって関数の値が定まるという意味なので3変数のスカラー関数f(x,y,z)として扱っても同じものを表します。
定ベクトルのうち、(0,0)を表すベクトルは
特にゼロベクトルと呼んで\(\overrightarrow{0}\)と表記する事もあります。
ただしこのサイトでは表記の簡略化のため、
ゼロベクトルはスカラー同様に0として表記をします。
ゼロベクトルは、図形上は向きがどこに向いているというわけでもなく、大きさも0であるベクトルという事になります。
ベクトル関数については座標成分で表す表記が分かりやすいかと思われます。
例えば変数xに対するてきとうな(x+1, x2)といったベクトルを考えると、このベクトルはxの値によってただ1つ定まります。そのようなベクトルをベクトル関数と呼ぶわけです。
いずれの場合も、「スカラー」という語を使う時には
「ベクトルではなくスカラー」という意味合いが強いです。
言い換えると、ベクトルを使わない議論をしている時にスカラーという語を敢えて使う事は少ないと言えます。
ベクトルには通常の数つまりスカラーを掛け算する事ができ、それは図形的にはベクトルの大きさだけを変化させる操作です。その事をベクトルの定数倍、あるいはスカラー倍とも言います。
$$ベクトルのスカラー倍:例えば\hspace{5pt}2\overrightarrow{AB},\hspace{5pt}-4\overrightarrow{AB},\hspace{5pt}\sqrt{3}\overrightarrow{AB}$$
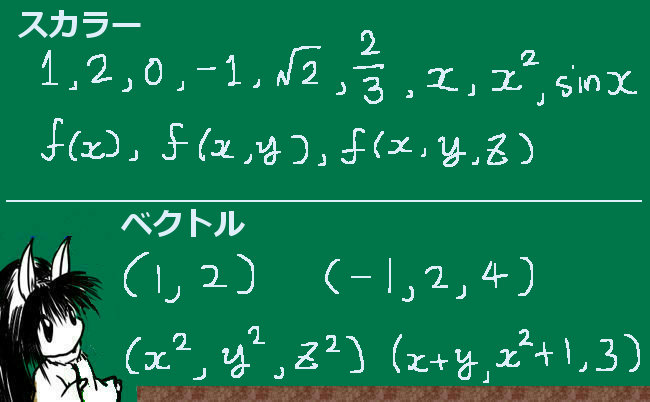
ベクトル関数にも1変数のもの、多変数のものがあります。
関数と区別する場合、成分が定数で構成されるベクトルを特に「定ベクトル」と呼ぶ事があります。
物理学等への応用も含めて、ベクトルに関して成立する定理、スカラー関数に関して言及している関係式などがあります。演算を組み合わせてベクトルとスカラーの関係が混じる事もあります。そういった時に、問題にしている対象がベクトルなのか「通常の実数等=スカラー」なのかが数学的な議論の際に重要となるのです。
例として、ベクトルに対して「内積」という演算をすると通常の数、つまりスカラーになります。
逆に、微積分も含んだ込み入った例ですが3変数のスカラー関数に対して「勾配」という演算をするとベクトル関数になります。
参考までにそのような「ベクトルなのかスカラーなのか」が特に重要になるものをいくつか整理して列挙すると次のようになります。
| 数学的・物理的な量 | 表記 | ベクトルか スカラーか | 定義の対象 |
| 内積(スカラー積) | \(\overrightarrow{A}\cdot\overrightarrow{B}\) | スカラー | 2つのベクトル |
| 外積(ベクトル積) | \(\overrightarrow{A}\times\overrightarrow{B}\) | ベクトル | 2つ以上の ベクトル |
| 勾配 (グレーディエント) | \(\mathrm{grad}\varphi\) \(\nabla\varphi\) | ベクトル | 3変数の スカラー関数 |
| 発散 (ダイバージェンス) | \(\mathrm{div}\overrightarrow{A}\) \(\nabla\cdot\overrightarrow{A}\) | スカラー | 1つのベクトル ※収束に対する 発散とは別物です。 |
| 回転 (ローテーション) | \(\mathrm{rot}\overrightarrow{A}\) \(\nabla\times\overrightarrow{A}\) | ベクトル | 1つのベクトル |