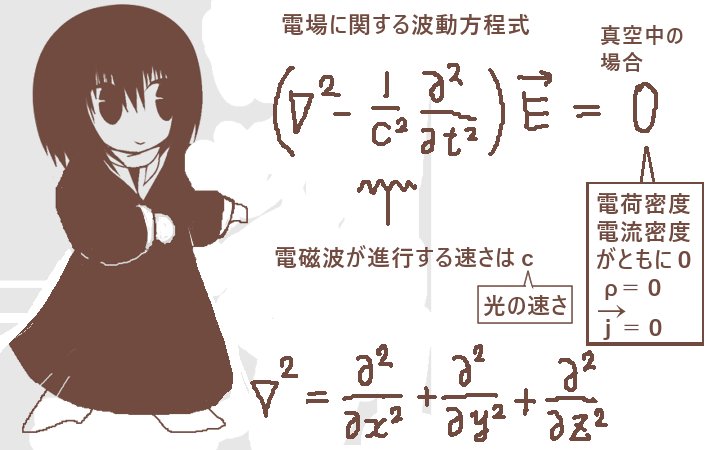
4つのマクスウェル方程式からは電磁波の式を得るための波動方程式およびそのもとになっている一般形の方程式の導出されます。
個々のマクスウェル方程式の性質や数式的な解析は他記事で詳しく説明しています。
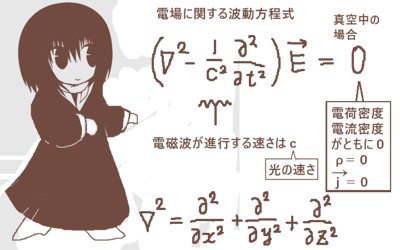
電場と磁場の波動方程式
結論を先に述べると、マクスウェル方程式からは
次のような電場と磁場のそれぞれについての波動方程式を導出できます。
真空中でρ=0および\(\overrightarrow{j}\)=0である条件では
電場と磁場のそれぞれについて成立する式は、
微分方程式としては次のように3次元の場合の波動方程式になります。
| 真空中における 電場の波動方程式 | \(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\right)\overrightarrow{E}=0\hspace{5pt}\) |
| 真空中における 磁場の波動方程式 | \(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\right)\overrightarrow{B}=0\hspace{5pt}\) |
ε0は真空の誘電率、μ0は真空の透磁率です。
係数については光の速さc=1/\(\sqrt{\epsilon_0\mu_0}\)を使って書いても同じです。
また、方程式を左辺と右辺に分けて書いても同じ微分方程式を表します。
| 別の書き方 | 左辺と右辺を分けた式 | 光の速さを使った時 |
| 電場 | \(\nabla^2\overrightarrow{E} =\epsilon_0\mu_0\frac{\Large\partial^2} {\Large\partial t^2}\overrightarrow{E}\) | \(\left(\nabla^2-\frac{\Large 1}{\Large c^2} \frac{\Large\partial^2}{\Large\partial t^2}\right)\overrightarrow{E}=0\) |
| 磁場 | \(\nabla^2\overrightarrow{B}=\epsilon_0\mu_0 \frac{\Large\partial^2}{\Large\partial t^2} \overrightarrow{B}\) | \(\left(\nabla^2-\frac{\Large 1}{\Large c^2}\frac{\Large\partial^2}{\Large\partial t^2}\right)\overrightarrow{B}=0\hspace{5pt}\) |
このように電場と磁場のそれぞれについて全く同じ形の式がマクスウェル方程式から導出されるわけですが、「真空中」という条件がついています。
これらの波動方程式には、もとになっている形があります。
マクスウェル方程式から法則と数学的な変形だけで直接的に導出される式は、
真空中に限らず一般の場合に成立する式です。
マクスウェル方程式から導出されるもとの形の式は次の通りです。 $$\left(\nabla^2-\epsilon_0\mu_0\frac{\partial^2}{\partial t^2}\right)\overrightarrow{E}=\frac{1}{\epsilon_0}\mathrm{grad}\rho+\mu_0\frac{\partial\overrightarrow{j}}{\partial t}$$ $$\left(\nabla^2-\epsilon_0\mu_0\frac{\partial^2}{\partial t^2}\right)\overrightarrow{B}=-\mu_0\mathrm{rot}\overrightarrow{j}$$ 一般の場合では電場と磁場の両方の式に電流密度が関係してくる事になります。
また、電場に対するスカラーポテンシャル(時間変動も含めた一般的な形)と磁場に対するベクトルポテンシャルを使った形の波動方程式と、そのもとになっている関係式もあります。
| 一般形 | ε0μ0を使って書いた時 | 光の速さを使った時 |
| 電場の式 | \(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\right)\phi=-\frac{\Large\rho}{\Large\epsilon_0}\) | \(\left(\nabla^2-\frac{\Large 1}{\Large c^2}\frac{\Large\partial^2}{\Large\partial t^2}\right)\phi=-\frac{\Large\rho}{\Large\epsilon_0}\) |
| 磁場の式 | \(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial}{\Large\partial t^2}\right)\overrightarrow{A}=-\mu_0\overrightarrow{j}\) | \(\left(\nabla^2-\frac{\Large 1}{\Large c^2}\frac{\Large\partial}{\Large\partial t^2}\right)\overrightarrow{A}=-\mu_0\overrightarrow{j}\) |
右辺を0とみなせる状況下では普通の波動方程式の形になります。
ただし、後述するこの式の解は右辺の電荷密度と電流密度が0でない場合も含んだ形の解です。
電磁波と光の関係
真空中の光の速さをcとすると実は数値的にε0μ0=1/(c2) が成立しています。
ε0=8.8542×10-12
μ0=1.2566×10-6
c=2.9979×108です。
1/(ε0μ0)≒1/(11.126187×10-18)≒8.9878×1016で、この平方根を考えると確かに真空中の光の速さとほぼ同じになります。
(物質中では光の速さは変わります。また、同じく誘電率と透磁率の値も物質中では変わります。)
さらに、波動方程式の解から分かる波(電磁波)が進行する速さは1/\(\sqrt{\epsilon_0\mu_0}\) です。
これは電磁現象に限らず一般の波動について言える事で、
例えば速さvで「波形」が進行するsin(kx-ωt)のような形の関数はω/k=vのもとで
\(\left(\frac{\Large\partial^2}{\Large\partial x^2}-\frac{\Large k^2}{\Large \omega^2}\frac{\Large\partial^2}{\Large\partial t^2}\right)\sin(kx-\omega t)=0\) を満たします。
この時に時間で偏微分する項の係数の逆数の平方根(プラスの値)はω/kで、
ωは角速度または角周波数で周期Tとω=2π/Tの関係があります。
またkは波数で波長λとk=2π/λの関係があるのでω/k=(2π/T){λ/(2π)}=λ/Tです。
ここで波の進行の速さvはv=λ/Tで表されるので、ω/k=vとなっています。
正弦波に限らず波動に対しては速さを考える事ができ、また正弦波でない波動を正弦波の重ね合わせとして考える方法もあります。
ε0μ0=1/(c2) からc=1/\(\sqrt{\epsilon_0\mu_0}\) なので、
電磁波が真空中を伝わる速さは光の速さに等しいという結果が得られます。
ところで光はマクロで見ると波なので、
物理学的には電磁波と光は波動として同じものであると捉えられています。
上記の関係式は、偶然にもほぼ一致するという事では無くて
「理論的にも実験的にも必ず成立する式である」
というのが物理学における解釈であるわけです。
いわゆる「目に見える光」は可視光とも呼ばれ、光の波長によって見える範囲が限定されている事が分かっています。(人と動物ではその範囲が違っていたりします。)
電磁波が光であるというのは基本的には「波動としては」という事であり、光は粒子(光子)でもあります。より詳しく言うと光は1つ1つは粒子として振る舞うけれども、それが多数集まると波として振る舞うようになります(干渉などの現象を起こすようになる)。ただし、電磁波と光を同一視できる関係は通常のマクロなスケールにおいてだけでなく、ミクロのスケールにおいても電場と磁場(のポテンシャル)から考えて光を量子力学的に考察する事がなされます。
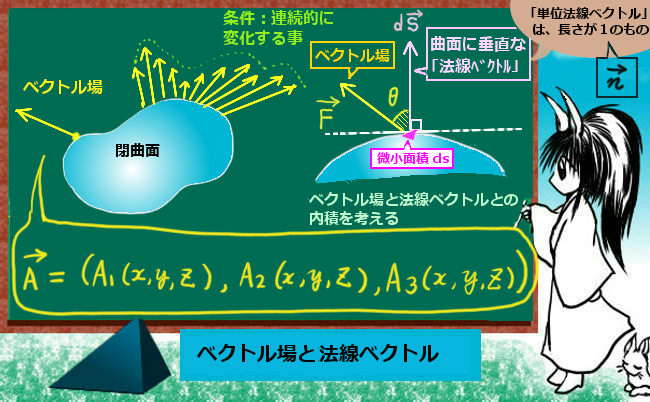
導出に必要な式および法則・記号・公式等
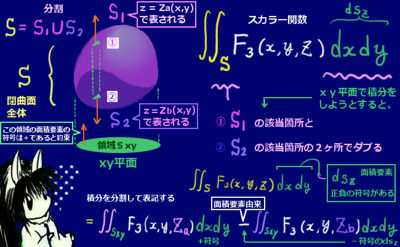
まず、マクスウェル方程式のうち時間微分を含む2式であるアンペールの法則と電磁誘導の法則の式に着目します。それらは、発散と回転の分類から言うと膜ウェル方程式の中で電場と磁場の回転に関する2式でもあります。
| マクスウェル方程式 (微分形) | 時間微分を含まない式 (電磁場の発散) | 時間微分を含む式 (電磁場の回転) |
| 電場の式 | 電場に関するガウスの法則 \(\mathrm{div}\overrightarrow{E}=\frac{\Large\rho}{\Large\epsilon_0}\) | アンペールの法則 \(\mathrm{rot}\overrightarrow{B}=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}\right)\) |
| 磁場の式 | 磁場に関するガウスの法則 \(\mathrm{div}\overrightarrow{B}=0\) | 電磁誘導の法則 \(\mathrm{rot}\overrightarrow{E}=-\frac{\Large\partial\overrightarrow{B}}{\Large\partial t}\) |
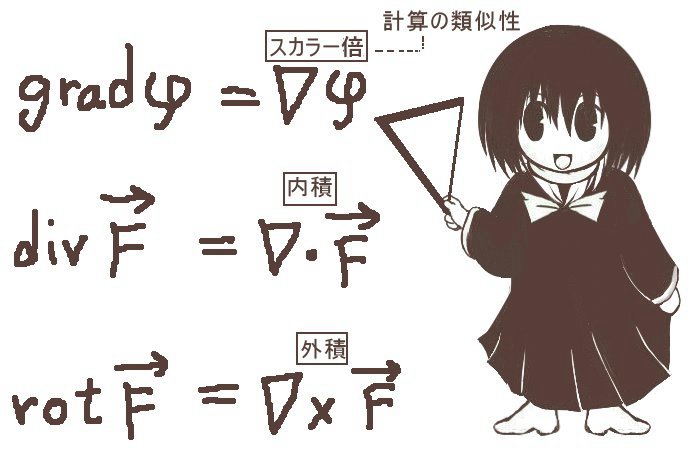
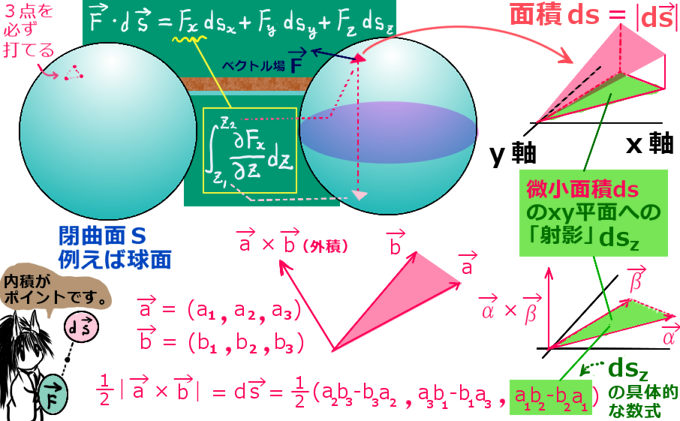
「ベクトル場の回転に対する回転」はベクトル解析での公式によりラプラス演算子(x,y,zでの2階偏微分を内積的な計算で作用させる演算子)を含む形になり、さらに途中計算で出てくる発散の項をガウスの法則(電場と磁場両方を使用)によって変形する事で波動方程式の形の微分方程式が得られる、というのが基本的な理論の流れです。
さらに「真空中」という条件を付ける事で電流密度の項を無視できるとすると比較的見やすい形の微分方程式となります。また、電場に対するスカラーポテンシャル(=電位)と磁場に対するベクトルポテンシャルからも同じく波動方程式を作る事ができて、特定の解を導出するにはそちらを使う方が簡単である場合もあります。
ナブラを使って書いた場合は次のようになります。
| マクスウェル方程式 (微分形・ナブラ表示) | 時間微分を含まない式 (電磁場の発散) | 時間微分を含む式 (電磁場の回転) |
| 電場の式 | 電場に関するガウスの法則 \(\nabla\cdot\overrightarrow{E}=\frac{\Large\rho}{\Large\epsilon_0}\) | 電磁誘導の法則 \(\nabla\times\overrightarrow{E}=-\frac{\Large\partial\overrightarrow{B}}{\Large\partial t}\) |
| 磁場の式 | 磁場に関するガウスの法則 \(\nabla\cdot\overrightarrow{B}=0\) | アンペールの法則 \(\nabla\times\overrightarrow{B}=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}\right)\) |
電磁波の式の導出の時には2階の時間微分を使うのでラプラス演算子を使うと表記が便利です。
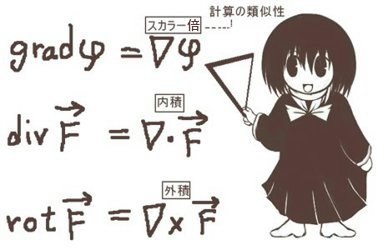
これはナブラによって表記できますがベクトルに対してはdiv, rot, grad の簡単な組み合わせでは書けません。
ただしスカラー場に対しては∇2φ = div(gradφ) の関係は成立します。
■「ベクトル場の回転」に回転をさらに作用させた時の式
| 通常表示 | $$\mathrm{rot}\left(\mathrm{rot}\overrightarrow{F}\right)=\mathrm{grad}\left(\mathrm{div}\overrightarrow{F}\right)-\nabla^2\overrightarrow{F}$$ |
| ナブラ使用時 | $$\nabla\times\left(\nabla\times\overrightarrow{F}\right)=\nabla\left(\nabla\cdot\overrightarrow{F}\right)-\nabla^2\overrightarrow{F}$$ |
■ラプラス演算子(∇2または△)
【これは記号として定義するものです。スカラーに対してもベクトルに対しても使えます。】
$$\nabla^2\overrightarrow{F}=△\overrightarrow{F}=
\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right)\overrightarrow{F}$$
$$=\frac{\partial^2\overrightarrow{F}}{\partial x^2}+\frac{\partial^2\overrightarrow{F}}{\partial y^2}+\frac{\partial^2\overrightarrow{F}}{\partial z^2}$$
■勾配ベクトルや発散に対する時間による偏微分
勾配や発散で使われる偏微分は座標変数によるものであり、
微分可能(ここでは2階まで)な関数であれば偏微分の順序は入れ換える事ができるので
$$\frac{\partial}{\partial t}(\mathrm{grad}\phi)=\mathrm{grad}\left(\frac{\partial\phi}{\partial t}\right)$$
$$\frac{\partial}{\partial t}\left(\mathrm{div}\overrightarrow{F}\right)=\mathrm{div}\left(\frac{\partial\overrightarrow{F}}{\partial t}\right)$$
のように式を変形できます。
■その他のベクトル解析の公式
- スカラー場φに対して、∇2φ=div (gradφ)
- \(r=\sqrt{(x-a_1)^2+(y-a_2)^2+(z-a_3)^2}\)に対して、
r≠0の時 ∇2(1/r)=div {grad(1/r)}=0 -
\(\overrightarrow{r}=(x-a_1,\hspace{2pt}y-a_2,\hspace{2pt}z-a_3)\)
\(\overrightarrow{R}=\frac{\Large 1}{\Large r}(x-a_1,\hspace{2pt}y-a_2,\hspace{2pt}z-a_3)\) の時、
grad(φ/r)=φgrad(1/r)+(1/r)gradφ
=\(-\frac{\Large\varphi}{\Large r^2}\overrightarrow{R}+\frac{\Large 1}{\Large r}\mathrm{grad}\varphi\) - grad(1/r)=-{1/(r3)} \overrightarrow{r}
- \(\mathrm{div}(r^n\overrightarrow{r})=(n+3)r^3\)
特にn=-1の時、\(\mathrm{div}\overrightarrow{R}=\mathrm{div}\left(\frac{\Large 1}{\Large r}\overrightarrow{r}\right)=2r^{-1}=\frac{\Large 2}{\Large r}\) - (∂/∂x)r= (x―a1)/r
- ∇2(φ1φ2)=∇2φ1+2(gradφ1)・(gradφ2)+∇2φ2
(積の微分公式を2回使う事に由来。第2項は内積です。) - div(φ\(\overrightarrow{F}\))=(gradφ)・\(\overrightarrow{F}\)+φdiv\(\overrightarrow{F}\)
以下ではラプラス演算子のみナブラ記号による∇2を使用し、
その他は div, grad 等の表記を使います。それらは全てナブラ記号で表現する事は可能です。
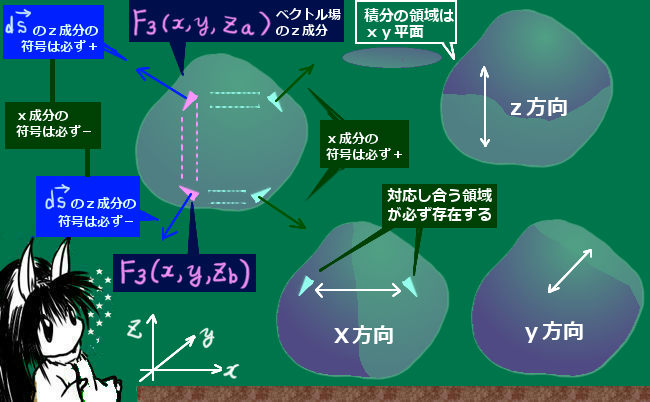
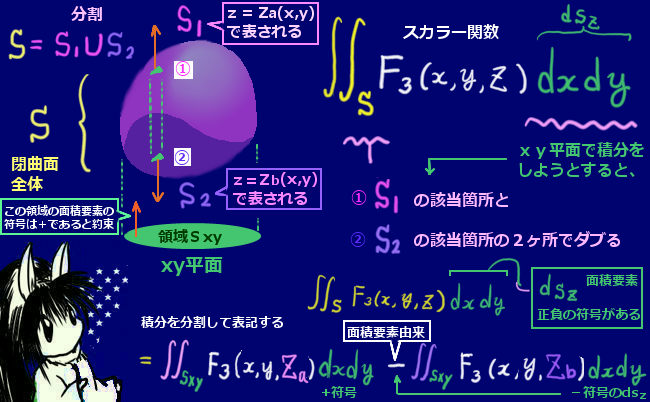
電場についての波動方程式の導出
電場と磁場の両方についてかなり似た操作でそれぞれについての波動方程式を導出できます。電磁誘導の法則とアンペールの法則をそれぞれ使いますが、実は計算の過程において電場と磁場の場合の両方でマクスウェル方程式のうち3つを使う事になります。
電場についての波動方程式を導出する時には、まず電磁誘導の法則の式から始めます。
| 電磁誘導の法則の微分形 | \(\mathrm{rot}\overrightarrow{E}=-\frac{\Large\partial\overrightarrow{B}}{\Large\partial t}\) |
| 両辺に回転を作用させる → 右辺は磁場の回転に対する 時間微分として書ける | \(\mathrm{rot}\left(\mathrm{rot}\overrightarrow{E}\right)=-\mathrm{rot}\left(\frac{\Large\partial\overrightarrow{B}}{\Large\partial t}\right)\) \(\Leftrightarrow\mathrm{rot}\left(\mathrm{rot}\overrightarrow{E}\right)=-\frac{\Large\partial}{\Large\partial t}\left(\mathrm{rot}\overrightarrow{B}\right)\) |
| アンペールの法則を 右辺に代入して 電場だけの式にする ◆時間による2階微分は ここで生じます。 | \(\mathrm{rot}\left(\mathrm{rot}\overrightarrow{E}\right)=-\frac{\Large\partial}{\Large\partial t}\left\{\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}\right)\right\}\) \(=-\mu_0\frac{\Large\partial\overrightarrow{j}}{\Large\partial t}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{E}}{\Large\partial t^2}\) |
| 左辺に公式を適用して変形 | \(\mathrm{grad}\left(\mathrm{div}\overrightarrow{E}\right)-\nabla^2\overrightarrow{E}=-\mu_0\frac{\Large\partial\overrightarrow{j}}{\Large\partial t}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{E}}{\Large\partial t^2}\) |
| 電場に関する ガウスの法則を左辺に代入 | \(\mathrm{grad}\left(\frac{\Large\rho}{\Large\epsilon_0}\right)-\nabla^2\overrightarrow{E}=-\mu_0\frac{\Large\partial\overrightarrow{j}}{\Large\partial t}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{E}}{\Large\partial t^2}\) \(\Leftrightarrow\frac{\Large 1}{\Large\epsilon_0}\mathrm{grad}\rho-\nabla^2\overrightarrow{E}=-\mu_0\frac{\Large\partial\overrightarrow{j}}{\Large\partial t}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{E}}{\Large\partial t^2}\) |
| 電場の項とその他を 左辺と右辺に分けて整理 | \(\Leftrightarrow\frac{\Large 1}{\Large\epsilon_0}\mathrm{grad}\rho+\mu_0\frac{\Large\partial\overrightarrow{j}}{\Large\partial t}=\nabla^2\overrightarrow{E}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{E}}{\Large\partial t^2}\) \(\Leftrightarrow\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\right)\overrightarrow{E}=\frac{\Large 1}{\Large\epsilon_0}\mathrm{grad}\rho+\mu_0\frac{\Large\partial\overrightarrow{j}}{\Large\partial t}\) |
| 真空中で電荷密度と 電流密度が0であると すると、 3次元の波動方程式 の形になる | 真空中を想定してρ=0および\(\overrightarrow{j}\)=0であるとすると \(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\right)\overrightarrow{E}=0\) \(\left(\Leftrightarrow\nabla^2\overrightarrow{E}=\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\overrightarrow{E}としても可\right)\) |
以上の式では、ε0μ0の項が出てきた時点で
光の速さcを使った形である1/(c2)に直して計算を進める事もできます。結果は同じです。
磁場についての波動方程式の導出
磁場についてもアンペールの法則から始めて。同様の手順でやれば波動方程式を導出できます。
| アンペール法則の微分形 | \(\mathrm{rot}\overrightarrow{B}=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}\right)\) |
| 両辺に回転を作用させる → 右辺は電場の回転に対する 時間微分として書ける | \(\mathrm{rot}\left(\mathrm{rot}\overrightarrow{B}\right)=\mathrm{rot}\left\{\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}\right)\right\}\) \(\Leftrightarrow\mathrm{rot}\left(\mathrm{rot}\overrightarrow{B}\right)=\mu_0\mathrm{rot}\overrightarrow{j}+\epsilon_0\mu_0\frac{\Large\partial}{\Large\partial t}\left(\mathrm{rot}\overrightarrow{E}\right)\) |
| 電磁誘導の法則を 右辺に代入して 磁場だけの式にする ◆時間による2階微分は 先ほどと同じく ここで生じます。 | \(\mathrm{rot}\left(\mathrm{rot}\overrightarrow{B}\right)=\mu_0\mathrm{rot}\overrightarrow{j}+\epsilon_0\mu_0\frac{\Large\partial}{\Large\partial t}\left(-\frac{\Large\partial\overrightarrow{B}}{\Large\partial t}\right)\) \(=\mu_0\mathrm{rot}\overrightarrow{j}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{B}}{\Large\partial t^2}\) |
| 左辺に公式を適用して変形 | \(\mathrm{grad}\left(\mathrm{div}\overrightarrow{B}\right)-\nabla^2\overrightarrow{B}=\mu_0\mathrm{rot}\overrightarrow{j}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{B}}{\Large\partial t^2}\) |
| 磁場に関する ガウスの法則を左辺に代入 (勾配の項は0になる。) | \(\mathrm{grad}0-\nabla^2\overrightarrow{B}=\mu_0\mathrm{rot}\overrightarrow{j}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{B}}{\Large\partial t^2}\) \(\Leftrightarrow-\nabla^2\overrightarrow{B}=\mu_0\mathrm{rot}\overrightarrow{j}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{B}}{\Large\partial t^2}\) |
| 磁場だけの項と それ以外を分けて 式を整理 | \(\Leftrightarrow-\nabla^2\overrightarrow{B}+\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{B}}{\Large\partial t^2}=\mu_0\mathrm{rot}\overrightarrow{j}\) \(\Leftrightarrow\nabla^2\overrightarrow{B}-\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{B}}{\Large\partial t^2}=-\mu_0\mathrm{rot}\overrightarrow{j}\) |
| 真空中で電荷密度と 電流密度が0であると すると、 3次元の波動方程式 の形になる | 真空中を想定して\(\overrightarrow{j}\)=0であるとすると \(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\right)\overrightarrow{B}=0\) \(\left(\Leftrightarrow\nabla^2\overrightarrow{B}=\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\overrightarrow{B}としても可\right)\) |
ポテンシャルによる電磁場の波動方程式の導出
電場のスカラーポテンシャルと磁場のベクトルポテンシャルから波動方程式(および一般の形の方程式)を作る事もできます。
この場合、まず電磁誘導の法則の微分形をベクトルポテンシャルを使った形にします。
| ベクトルポテンシャルで 表した磁場 | 電磁誘導の法則の微分形 | ベクトルポテンシャルで 表した電磁誘導の法則 |
| \(\mathrm{rot}\overrightarrow{A}=\overrightarrow{B}\) | \(\mathrm{rot}\overrightarrow{E}=-\frac{\Large\partial\overrightarrow{B}}{\Large\partial t}\) | \(\mathrm{rot}\overrightarrow{E}= -\frac{\Large\partial}{\Large\partial t}\mathrm{rot}\overrightarrow{A}\) \(\Leftrightarrow\hspace{2pt} \mathrm{rot} \left(\overrightarrow{E}+\ \frac{\Large\partial\overrightarrow{A}}{\Large\partial t}\right)=0\) |
ここで、静電場に対する渦無しの法則を考えた時と同様に
「回転が0であるベクトル場」は何かのスカラー場の勾配として書けます。
そのスカラー場を考えて磁場の時間変化が無い時は電位に等しくなるように-Φとします。そのようにおいた式の両辺の発散を考えると式をラプラス演算子で表せます。
| スカラー場Φを考えます。 (一般の場合の電場に対する スカラーポテンシャル) | \(-\mathrm{grad}\phi=\overrightarrow{E}+ \frac{\Large\partial\overrightarrow{A}}{\Large\partial t}\)となるΦが存在する。 |
| 両辺の発散を考えます。 すると、左辺は ラプラス演算子∇2で 表す事ができます。 | \(-\mathrm{div}\left(\mathrm{grad}\phi\right)=\mathrm{div}\left(\overrightarrow{E}+\frac{\Large\partial\overrightarrow{A}}{\Large\partial t}\right)\) \(\Leftrightarrow -\nabla^2\phi=\mathrm{div}\left(\overrightarrow{E}+\ \frac{\Large\partial\overrightarrow{A}}{\Large\partial t}\right)\) (※スカラー場に対しては∇2Φ=div(gradΦ)が成立。 ベクトルに対しては同様の簡単な関係式は作れません。) |
ところでベクトルポテンシャルのゲージ条件はまだ何も決めていないので、少し唐突で無理やり感もあるように見えるかもしれませんが次のゲージ条件を課します。
このゲージ条件を特に「ローレンツ条件」と呼ぶ事があります。
$$\mathrm{div}\overrightarrow{A}+\epsilon_0\mu_0\frac{\partial\phi}{\partial t}=0$$
$$\left(あるいは光の速さcを使って\mathrm{div}\overrightarrow{A}+\frac{1}{c^2}\frac{\partial\phi}{\partial t}=0\right)$$
下記では、この式の時間微分を考えたものと、勾配を考えたものも使用します。
■時間微分をしたもの
$$\frac{\partial}{\partial t}\mathrm{div}\overrightarrow{A}+\epsilon_0\mu_0\frac{\partial^2\phi}{\partial t^2}=0$$
$$\Leftrightarrow\mathrm{div}\frac{\partial\overrightarrow{A}}{\partial t}+\epsilon_0\mu_0\frac{\partial^2\phi}{\partial t^2}=0$$
$$\Leftrightarrow\mathrm{div}\frac{\partial\overrightarrow{A}}{\partial t}=-\epsilon_0\mu_0\frac{\partial^2\phi}{\partial t^2}$$
■勾配を考えたもの
$$\mathrm{grad}\left(\mathrm{div}\overrightarrow{A}\right)+\mathrm{grad}\left(\epsilon_0\mu_0\frac{\partial\phi}{\partial t}\right)=0$$
$$\Leftrightarrow\mathrm{grad}\left(\mathrm{div}\overrightarrow{A}\right)=-\left(\epsilon_0\mu_0\frac{\partial}{\partial t}\mathrm{grad\phi}\right)$$
$$電磁誘導の法則に由来する-\mathrm{grad}\phi=\overrightarrow{E}+\frac{\partial\overrightarrow{A}}{\partial t}を使って、$$
$$\mathrm{grad}\left(\mathrm{div}\overrightarrow{A}\right)=
\epsilon_0\mu_0\frac{\partial}{\partial t}\left(\overrightarrow{E}+\frac{\partial}{\partial t}\overrightarrow{A}\right)
=
\epsilon_0\mu_0\frac{\partial\overrightarrow{E}}{\partial t}+\epsilon_0\mu_0\frac{\partial^2\overrightarrow{A}}{\partial t^2}$$
磁場に関するガウスの法則はベクトルポテンシャルを考える事自体に使っている事に注意すると、先ほどの電磁誘導の法則をポテンシャルで考えた式を考えた時点でまだ使っていないマクスウェル方程式は電場に関するガウスの法則とアンペールの法則です。
そこで電磁誘導の法則から得られたベクトルポテンシャルとスカラーポテンシャルの関係式を、同じくポテンシャルで表した電場に関するガウスの法則とアンペールの法則に代入して上記のゲージ条件を適用すると波動方程式が得られます。
電場のスカラーポテンシャルの場合
| 電場に関するガウスの法則(微分形) | \(\mathrm{div}\overrightarrow{E}=\frac{\Large\rho}{\Large\epsilon_0}\) |
| 一般形のスカラーポテンシャルで表した 電場に関するガウスの法則 | \(-\mathrm{div}\left(\mathrm{grad}\phi+\frac{\Large\partial\overrightarrow{A}}{\Large\partial t}\right)=\frac{\Large\rho}{\Large\epsilon_0}\) |
| 【ゲージ条件から】 \(\mathrm{div}\frac{\Large\partial\overrightarrow{A}}{\Large\partial t}=-\epsilon_0\mu_0\frac{\Large\partial^2\phi}{\Large\partial t^2}\) 【スカラー場で成立する式】 ∇2Φ=div(gradΦ) | \(-\nabla^2\phi+\epsilon_0\mu_0\frac{\Large\partial^2\phi}{\Large\partial t^2}=\frac{\Large\rho}{\Large\epsilon_0}\) \(\Leftrightarrow\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\right)\phi=-\frac{\Large\rho}{\Large\epsilon_0}\) |
| 電荷密度を0とみなせる 場合には波動方程式の形 | \(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\right)\phi=0\) |
この結果は、ベクトルではなくスカラー場の波動方程式になっています。
また、ポテンシャルで考える場合には電磁場を考える地点での電荷密度を0と考えずに一般形のまま計算をする事がよくあります。さらに、後述するこの微分方程式の解となる式においては電磁場およびポテンシャルを考えている地点とは別の領域に存在する電荷密度の分布を考えます。
それは電位やベクトルポテンシャルを考える時にも使う考え方ではありますが、紛らわしい事もあり注意が必要な点とも言えます。
磁場のベクトルポテンシャルの場合
磁場の場合はアンペールの法則の微分形から始めて、計算式が一見少し複雑になりますが波動方程式の形に変形できます。
| アンペールの法則の微分形 | \(\mathrm{rot}\overrightarrow{B}=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}\right)\) |
| \(\overrightarrow{B}=\mathrm{rot}\overrightarrow{A}\)を代入 回転に関する公式により変形 | \(\mathrm{rot}\left(\mathrm{rot}\overrightarrow{A}\right)=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}\right)\) \(\Leftrightarrow\mathrm{grad}\left(\mathrm{div}\overrightarrow{A}\right)-\nabla^2\overrightarrow{A}=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}\right)\) |
| 【ゲージ条件から】 \(\mathrm{grad}\left(\mathrm{div}\overrightarrow{A}\right)\) \(=\epsilon_0\mu_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}+\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{A}}{\Large\partial t^2}\) 代入すると電場の項 (変位電流の部分) が消えます。 | \(\epsilon_0\mu_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}+\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{A}}{\Large\partial t^2}-\nabla^2\overrightarrow{A}\) \(=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\Large\partial\overrightarrow{E}}{\Large\partial t}\right)\) 両辺に同じ係数の変位電流の項があり、消える。 \(\epsilon_0\mu_0\frac{\Large\partial^2\overrightarrow{A}}{\Large\partial t^2}-\nabla^2\overrightarrow{A}=\mu_0\overrightarrow{j}\) |
| 整理するとこの形 | \(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial}{\Large\partial t^2}\right)\overrightarrow{A}=-\mu_0\overrightarrow{j}\) |
| 電流密度を0とみなせる 場合には波動方程式の形 | \(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial}{\Large\partial t^2}\right)\overrightarrow{A}=0\) |
ここでは静電場に限定せず一般の電場を考えているので、
電場のスカラーポテンシャルは\(\overrightarrow{E}=-\mathrm{grad}\phi\)(静電場の場合)ではなく、
上記の
\(-\mathrm{grad}\phi=\overrightarrow{E}+\frac{\Large\partial\overrightarrow{A}}{\Large\partial t}\)
\(
\Leftrightarrow\overrightarrow{E}=-\mathrm{grad}\phi-\frac{\Large\partial\overrightarrow{A}}{\Large\partial t}\)を使用しています。
平面波解として得られる電磁波の式
ベクトルに対する偏微分方程式も、
成分ごとに見ればスカラー関数に対する偏微分方程式になります。例えば、
\(\left(\nabla^2-\epsilon_0\mu_0\frac{\Large\partial^2}{\Large\partial t^2}\right)E_x=0\)などです。
これの解の1つとして比較的簡単で代表的なものは次のような平面波です。
(以下、c=1/\(\sqrt{\epsilon_0\mu_0}\)であるとします。)
2階まで微分可能である任意の2つの関数U(u)とW(w)を使って、
変数をz-ctとz+ctとして電場のx成分について
Ex=U(z-ct)+W(z+ct)
のような関数形を考えます。(xとyに関しては変数ではない関数。)
すると、実はこれは真空中の電場に関する波動方程式の解になっており、
平面電磁波あるいは単に平面波を表すものになります。
これは一体何を言っているのかという話ですが、U(z-ct)は進行波でW(z+ct)が反射波を表します。さらにxとyは変数ではないという関数形である事は「z軸方向に進行していく」事を表します。
※この段階では「波」と言っても周期関数に限らず、何らかの「波形」の関数が時間ごとに進行していくものです。また、zだけが特別扱いというわけではなく、U(y-ct)+W(y+ct)のような関数を考えればこれはy方向に進行していく「波」を表します。
いずれにしても、定数cはそれが進行していく速さを表すわけで、ε0μ0=1/(c2)の関係式によって「電磁波が進行する速さは光の速さに等しい」という事を表しています。
最初のほうで少し触れたように、具体的な正弦波などの関数を想定する場合には波としての速さと関数に対する変数の部分(位相)との間に関係式を作る必要な事があります。
例えばここでの場合で進行波としての正弦関数を考える時には、
振幅E0と波数 k に対してE0sin(ku)の形の式にu=zーctを代入して
E0sin(kz-kct)=E0sin(kz-ωt)のようにします。
上記の式が確かに波動方程式の解になっているかどうかについては直接計算すればよいのですが、意外と少し面倒くさくて変数と微分の関係などに注意する必要があります。(微分をしていくだけの計算問題になるので、記述は後回しにします。)
電場のx成分とy成分が平面電磁波を表す形であるとして、
磁場に関してもx瀬尾文とy成分が同様の形であるとします。
∂Ex/∂x=0と∂Ex/∂y=0および∂Ey/∂x=0と∂Ey/∂y=0などの関係をマクスウェル方程式に戻って当てはめていくと、他の成分についても決定するものが複数あります。
それらを整理すると次のようになります。
| Ex=U(z-ct)+W(z+ct)および Ey=Uy(z-ct)+Wy(z+ct)から | ∂Ex/∂x=∂Ex/∂y=0 ∂Ey/∂x=∂Ey/∂y=0 |
| 磁場に関しても波動方程式は 同じ形なのでBxとByは zとtのみの関数だとして | ∂Bx/∂x=∂Bx/∂y=0 ∂By/∂x=∂By/∂y=0 |
| 電場に関するガウスの法則で 電荷密度ρが0のもとで | ∂Ex/∂x+∂Ey/∂y+Ez/∂z=0 により∂Ez/∂z=0 |
| 磁場に関するガウスの法則より | ∂Bx/∂x+∂By/∂y+Bz/∂z=0 により∂Bz/∂z=0 |
| Ez/∂z=0を波動方程式に当てはめて | ∂Ez/∂t=0 |
| 電磁誘導の法則の微分形の z成分を考えると | ∂Ey/∂x-∂Ex/∂y=-∂Bz/∂tより ∂Bz/∂t=0 |
∂Ez/∂z=0である事を踏まえて、
さらにEzがxとyに関しても定数だとしても波動方程式を満たすのでそのようなものを考えます。
つまりその場合は∂Ez/∂x=∂Ez/∂y=0です。
その条件下では、電磁誘導の法則のx成分とy成分から
∂Ey/∂z=∂Bx/∂t
∂Ex/∂z=-∂By/∂t
という関係が得られます。
その事から、その条件下で電場と磁場のx成分とy成分の関係は次のようになります。
| Ex =Ux(z-ct)+Wx(z+ct) | Bx =(1/c){-Uy(z-ct)+Wy(z+ct)} | ∂Ey/∂z =∂Bx/∂t |
| Ey =Uy(z-ct)+Wy(z+ct) | By =(1/c){Ux(z-ct)-Wx(z+ct)} | ∂Ex/∂z =-∂By/∂t |
もし進行波と反射波が別々のベクトルであるとするなら、電磁波の進行方向に対して垂直な平面内で進行波における電場と磁場は直交し、反射波における電場と磁場も直交する事になります。
| 進行波と反射波が 別々のベクトル という仮定 | 電場 | 磁場 | 進行方向に垂直な 平面内での電場と磁場の内積 |
| 入射波 | Ex1=Ux Ey1=Uy | Bx1=-Uy/c By1=Ux/c | (1/c)(-UxUy+UxUy)=0 |
| 反射波 | Ex2=Wx Ey2=Wy | Bx2=Wy/c By2=-Wx/c | (1/c)(WxWy-WxWy)=0 |
電磁波における電場と磁場の成分が正弦波あるいはその重ね合わせであると考えると、平面電磁波の電場と磁場の成分が進行方向に垂直である事は「波数ベクトル」との内積が0になる事でも示せます。
Ex=U(z-ct)+W(z+ct)が波動方程式の解である事を見るには次にようにします。
Z1=z-ct,Z2=z+ctとするとEx=U(Z1)+W(Z2)であり,
(∂/∂t)Ex=(dU/dZ1) (∂Z1/∂t)+(dW/dZ2) (∂Z2/∂t)
=-c(dU/dZ1)+(dW/dZ2)
【※もしU(P(z,t),Q(z,t))のような関数なら
∂U/∂t=(∂U/∂P)(∂P/∂t)+(∂U/∂Q)(∂Q/∂t)のような計算になります。
ここでは∂z/∂t=0なので見かけ上はその項が無い形になっています。
】
さらに計算すると、
(∂2/∂t2)Ex=-c(d2U/dZ12) (∂Z1/∂t)+c(d2U/dZ22) (∂Z2/∂t)
=-c2(d2U/dZ12)+c2(d2U/dZ22)
同様にして、
(∂2/∂z2)Ex=(∂/∂z){(dU/dZ1) (∂Z1/∂z)+(dW/dZ2) (∂Z2/∂z)}
=(∂/∂z){(dU/dZ1)+(dW/dZ2)}
=(d2U/dZ12) (∂Z1/∂z)+(d2U/dZ22) (∂Z2/∂t)
=(d2U/dZ12)+(d2U/dZ22)
よって、{∂2/∂z2-(1/c2) (∂2/∂t2)}Ex=0であり、
Ex=U(Z1)+W(Z2)はzとtだけの関数という設定なので
xとyによる偏微分は0である事に注意すると
{∇2-(1/c2) (∂2/∂t2)}Ex=0
を満たす事が分かります。
y成分についても同じ変数の形Z1,Z2と、異なる関数形Uy,Wyを考えて
Ey=Uy(Z1)+Wy(Z2)
というzとtだけの関数として計算すれば波動方程式を満たします。
ポテンシャルによる計算から得られる電磁波の式
ポテンシャルを使ったほうの波動方程式を解くと、少し別の形の数式での電磁波の式を得ます。
スカラーポテンシャルにしてもベクトルポテンシャルにしても、静電場と静磁場の場合には積分の形はとるけれども一応微分方程式の解としてポテンシャルを数式で表す事は可能です。
そして前述のポテンシャルの波動方程式および一般の形の式(ρ≠0等の場合)でも、実はかなり似た形の式が解になります。
静電場や静磁場に限定した時と異なる点は、電荷密度と電流密度に変数として加わる「時間」の部分です。そしてその時間変数は、空間中で電磁波による電磁場を考えている地点と、電磁場を作っている電荷や電流がある領域との時間変化における「時刻」のずれが反映された形にする必要がある事が知られています。
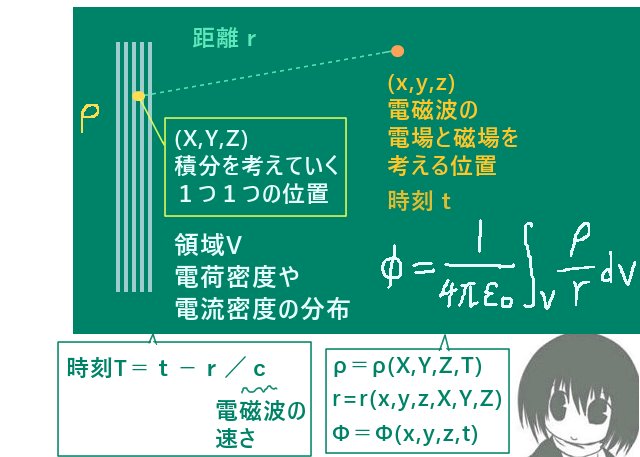
具体的には、まず平面波を表す解で得られた電磁波の速さc=\(\sqrt{\epsilon_0\mu_0}\)が一般に適用できるものだと仮定して、電荷や電流の各位置から電磁場を考える位置までの距離をrとします(これは関数)。
そして、電荷や電流の時間変数をtとした時に、その変数をt-r/cに置き換えたものを考えます。
これはrという位置座標の関数を含むのでx,y,z,tの関数です。
そこでT(x,y,z,t)=t-r/cとおいておきます。
前述のポテンシャルで表した場合の真空中の波動方程式、および電荷密度あるいは電流密度が0でない場合の式における解の1つは次式で表されます。
ポテンシャルであるΦと\(\overrightarrow{A}\),および積分していないρや\(\overrightarrow{j}\)は
x,y,zおよびtの関数であるとします。
電荷あるいは電流密度が分布する領域をVとして、
dv=dXdYdXのもとで
(x,y,z)と(X,Y.Z)の距離をrとおき、
T=t-r/c のもとで
積分中の電荷密度ρと電流密度\(\overrightarrow{j}\)はX,Y,Z,T(=t-r/c)の関数であるとします。
| 式と解 | もとの式(波動方程式を含む一般形) | 解となるポテンシャル |
| 電場 | $$\left(\nabla^2-\epsilon_0\mu_0\frac{\partial^2}{\partial t^2}\right)\phi=-\frac{\rho}{\epsilon_0}\hspace{20pt}$$ | $$\phi=\frac{1}{4\pi\epsilon_0}\int_V\frac{\rho}{r}dv$$ |
| 磁場 | $$\left(\nabla^2-\epsilon_0\mu_0\frac{\partial}{\partial t^2}\right)\overrightarrow{A}=-\mu_0\overrightarrow{j}$$ | $$\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_V\frac{\overrightarrow{j}}{r}dv$$ |
これらの解は遅延ポテンシャル(retarded potential)とも呼ばれます。
積分の中身とそれ以外の部分で関数が何の変数であるかを整理すると次のようになります。
| ◆x,y,z,tの関数 電場や磁場を考える位置と時間 | ◆X,Y,Z,Tの関数【積分の中身】 電荷密度や電流密度の分布内の位置 |
| \(\phi=\phi(x,y,z,t)\) \(\overrightarrow{A}=\overrightarrow{A}(x,y,z,t)\) | \(\rho=\rho(X,Y,Z,T)\) \(\overrightarrow{j}=\overrightarrow{j}(X,Y,Z,T)\) |
時間変数に関しては T=T(x,y,z,X,Y,Z,t)であり、x,y,z,X,Y,Z,t は互いに独立な変数です。
また、\(r=r(x,y,z,X,Y,Z)\) であり、積分に関してはx,y,zは定数扱いです。
また、ポテンシャルから計算できる電場と磁場は次のようになります。
■電場
\(-\mathrm{grad}\phi=\overrightarrow{E}+ \frac{\Large\partial\overrightarrow{A}}{\Large\partial t}\Leftrightarrow\overrightarrow{E}=-\mathrm{grad}\phi-\frac{\Large\partial\overrightarrow{A}}{\Large\partial t}\)である事と、
電荷密度の分布は領域内で微分可能(従って連続)である関数形である事
(X,Y,Zが積分変数の被積分関数をx,y,zやtで偏微分してから積分可能)、
ベクトルポテンシャルの項は静磁場の時の式を使ってε0μ0=1/(c2 )の関係に注意します。
積分内で電荷密度と電流密度は先ほどと同じくX,Y,Z,Tの関数とします。
電場と磁場はx,y,z,tの関数です。また、\(\overrightarrow{R}=\frac{\Large 1}{\Large r}(x-X,\hspace{2pt}y-Y,\hspace{2pt}z-Z)\)とします。
$$\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_V\frac{\overrightarrow{j}}{r}dv=\frac{1}{4\pi\epsilon_0c^2}\int_V\frac{\overrightarrow{j}}{r}dvに注意して、$$
$$\overrightarrow{E}=-\mathrm{grad}\left(\frac{1}{4\pi\epsilon_0}\int_V
\frac{\rho}{r}dv\right)-\frac{\partial\overrightarrow{A}}{\partial t}$$
$$=\frac{1}{4\pi\epsilon_0}\int_V\left(\frac{\rho}{r^2}\overrightarrow{R}+\frac{\rho}{cr}\overrightarrow{R}-\frac{\partial }{\partial t}\frac{\overrightarrow{j}}{c^2r}\right)dv$$
■磁場
回転と外積ベクトルの関係に注意して計算すると\(\mathrm{rot}\overrightarrow{A}=\overrightarrow{B}\)により、次式になります。
積分中のクロス「×」記号は外積の意味です。
$$\overrightarrow{B}=\mathrm{rot}\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_V\left(\frac{\overrightarrow{j}}{r^2}\times\overrightarrow{R}+\frac{\overrightarrow{j}}{cr}\times\overrightarrow{R}\right)dv$$
これらの式は、時間変化する電荷密度や電流密度(具体的には周波数の高い交流電流など)によって電磁波を形成する電場と磁場の関数形を具体的に表せる事を意味しています。
また、電磁波が正弦波のような周期関数になるかどうかも、領域Vに分布する電荷密度や電流密度の形で決まる事になります。
式に積分が含まれている事を見ると分かる通り、実際に詳しく考察する時には工夫が必要です。
これらの式においてrが十分大きい時には1、/rに比例する項に比べて他の項をほぼ0とみなして近似する事ができます。
遅延ポテンシャルが解となっている事の確認計算
先ほどの「遅延ポテンシャル」が波動方程式を作るポテンシャルの式を満たすのかどうかは、少々長ったらしい計算が必要ですが確認する事ができます。
まず、スカラーポテンシャルのほうを見ます。ベクトルポテンシャルについても、成分ごとに見ればスカラーポテンシャルの時と同様に計算ができます。
∇2と発散、勾配はいずれもx,y,zの変数での偏微分を行うものとします。
| 何を計算していくのか? | 電場のスカラーポテンシャルについて |
| 電磁場に関する 波動方程式の一般形となるこの式に対して | $$\left(\nabla^2-\epsilon_0\mu_0\frac{\partial^2}{\partial t^2}\right)\phi=-\frac{\rho}{\epsilon_0}$$ |
| このように表されるΦを代入して 式が満たされるのかを検証。 | $$\phi=\frac{1}{4\pi\epsilon_0}\int_V\frac{\rho}{ r}dv$$ |
積分の中身ρ/rについてラプラス演算子を作用させると、公式を使って
∇2(ρ/r)=∇2ρ+2{grad(1/r)}・(gradρ)+ρ∇2(1/r)
ここでρ∇2(1/r)の項に関してはr≠0であれば∇2(1/r)=0になります。【ただし、電磁波の電場を考える点(x,y,z)が領域V内にあるような状況(r=0という事)があっても、極限値として考えれば実はこの項は積分をした時に有限の値になります。】
そこで、計算が必要なのは残りの2項になります。
- ∇2ρ
- 2{grad(1/r)}・(gradρ)
ρとrは積分の中にあり、
ρ=ρ(X,Y,Z,T) と r=r(x,y,z,X,Y,Z) の変数に注意して計算します。
勾配ベクトルの内積部分の計算
勾配ベクトルの内積部分の計算を先に見ます。
積分内のρの変数であるX,Y,Z,Tのうち
x,y,zの関数であるのはTだけです。
∂ρ/∂x=(∂ρ/∂T) (∂T/∂x)
【本来、数学的な計算としては∂ρ/∂x=(∂ρ/∂T) (∂T/∂x)+(∂ρ/∂X) (∂X/∂x)+・・・で、
∂X/∂x=0,∂Y/∂x=0,∂Z/∂x=0なので(∂ρ/∂X)(∂X/∂x)等の項は0】
ここでT=t-r/cなので、
∂T/∂x=-(∂/∂x) (r/c)=-(x-X)/(rc) であり、
∂ρ/∂x=(∂ρ/∂T) (∂T/∂x)=-{(x-X)/(rc)}(∂ρ/∂T)
他方でT=t-r/cをtで偏微分すると∂T/∂t=1であり、
∂x/∂tや∂X/∂t等は0なので
∂ρ/∂t=(∂ρ/∂T) (∂T/∂t)+(∂ρ/∂x) (∂x/∂t)+(∂ρ/∂y) (∂y/∂t)+・・・
=(∂ρ/∂T) (∂T/∂t)
=∂ρ/∂T
独立変数の関係にあるのはx,y,z,X,Y,Z,tであるので
【考えている位置自体は運動していないのでx=x(t)等の関係は無く、xとtは定数の関係。】
x,y,z,X,Y,Zに対するtの偏微分は0(例えば∂x/∂t=0など)
つまり∂ρ/∂t=∂ρ/∂Tの関係があるので
先ほどの式は
∂ρ/∂x=-{(x-X)/(rc)}(∂ρ/∂t)と書けます。
【Tによる偏微分ではなくtによる偏微分でも同じ結果になるという事。】
これらの事はyやzについても同様の計算で、時間変数による偏微分はtで書けます。
∂ρ/∂y=-(y-Y)(∂ρ/∂t)/(rc)
∂ρ/∂z=-(z-Z)(∂ρ/∂t)/(rc)となるので
\(\overrightarrow{R}=\frac{\Large 1}{\Large r}(x-X,y-Y,z-Z)\) とすると、
gradρ=-(1/c) (∂ρ/∂t)\(\overrightarrow{R}\)
ここで、grad(1/r)=-\(\overrightarrow{R}\)/(r2)であり、
\(\overrightarrow{R}\)の大きさは1である事に注意すると∇2(Φ/r)の式中の内積計算は
2{grad(1/r) }・(gradρ)={-2/(r2) } {-(1/c) (∂ρ/∂t) }
={2/(cr2) } (∂ρ/∂t)
【この項は、あとで消えます。】
電荷密度に対する∇2ρの部分の計算
また、スカラー関数については∇2ρ=div(gradρ)なので、div(gradρ)を計算します。
grad(∂ρ/∂t)については先ほどのgradρ=-(1/c) (∂ρ/∂t)\(\overrightarrow{R}\)と同じ形の計算が可能で、
grad(∂ρ/∂t)gradρ=-(1/c) (∂2ρ/∂t2)\(\overrightarrow{R}\)
\(\overrightarrow{R}\) の大きさはr/r=1である事に注意して、
公式div(φ\(\overrightarrow{F}\))=(gradφ)・\(\overrightarrow{F}\)+Φdiv\(\overrightarrow{F}\) および
div\(\overrightarrow{R}\)=2/rも使用すると次のようになります。
$$\nabla^2\left(\mathrm{grad}\rho\right)=\mathrm{div}\left(\mathrm{grad}\rho\right)$$
$$=\mathrm{div}\left\{-\frac{1}{c}\frac{\partial \rho}{\partial t}\overrightarrow{R}\right\}=-\frac{1}{c}\left\{\left(\mathrm{grad}\frac{\partial \rho}{\partial t}\right)\cdot\overrightarrow{R}+\frac{\partial \rho}{\partial t}\mathrm{div}\overrightarrow{R}\right\}$$
$$=-\frac{1}{c}\left\{-\frac{1}{c}\left(\frac{\partial^2 \rho}{\partial t^2}\overrightarrow{R}\right)\cdot\overrightarrow{R}+\frac{2}{r}\frac{\partial \rho}{\partial t}\right\}$$
$$=\frac{1}{c^2}\frac{\partial^2 \rho}{\partial t^2}-\frac{2}{cr}\frac{\partial \rho}{\partial t}$$
これを見ると、式の最後の形の2項目の-{2/(cr)} (∂ρ/∂t)に1/rを乗じると
先ほどの2{grad(1/r)}・(gradρ)={2/(cr2)} (∂ρ/∂t)に加えれば0になる事が分かります。
よって、ここで式を一度整理すると次式になります。
$$\nabla^2\left(\frac{\rho}{r}\right)=\frac{1}{r}\nabla^2\left(\mathrm{grad}\rho\right)+2\left\{\mathrm{grad}\left(\frac{1}{r}\right)\right\}\cdot(\mathrm{grad}\rho)+\rho\nabla^2\left(\frac{1}{r}\right)$$
$$=\frac{1}{c^2r}\frac{\partial^2 \rho}{\partial t^2}+\rho\nabla^2\left(\frac{1}{r}\right)$$
この式に1/(4πε0)を乗じて領域Vで体積積分します。
【ベクトルポテンシャルの成分の時には、ここでμ0/(4π)を乗じます。】
$$\frac{1}{4\pi\epsilon_0}\int_V\nabla^2\left(\frac{\rho}{r}\right)dv=\frac{1}{4\pi\epsilon_0}\int_V\left\{\frac{1}{c^2r}\frac{\partial^2 \rho}{\partial t^2}+\rho\nabla^2\left(\frac{1}{r}\right)\right\}dv$$
$$整理すると、\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\left(\frac{1}{4\pi\epsilon_0}\int_V\frac{\rho}{r}dv\right)=\frac{1}{4\pi\epsilon_0}\int_V\rho\nabla^2\left(\frac{1}{r}\right)dv$$
r≠0の時はρ∇2(1/r)=0なので波動方程式の形を満たす事が分かります。
$$r\neq 0であるなら、\left(\nabla^2-\frac{1}{c^2}\frac{\partial^2}{\partial t^2}\right)\left(\frac{1}{4\pi\epsilon_0}\int_V\frac{\rho}{r}dv\right)=0$$
ではr=0になるような点を含む場合ではどうかというと、その場合でも遅延ポテンシャルの形の式は積分をした時に極限を考える形でρ≠0の場合の方程式を満たします。(デルタ関数で考える事も多い。)また、遅延ポテンシャルによる解は実はかなり一般性を持った形の解でもあります。