代数学での「体」【たい】の拡大という考え方について説明します。
英:拡大体 extension field 部分体 subfield
【体:field 日本語訳は、おそらくドイツ語での名称から。 】
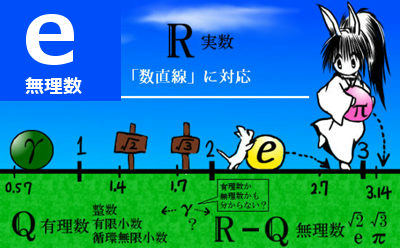
「体」の拡大とは?
実数に対してi2=-1となるiを導入して複素数a+biを考える事や、
有理数に対して平方根などを使ってp+q\(\sqrt{2}\) を考える事を、「拡大」と言います。
実数や有理数は「体」(たい)という構造の集合に分類され、拡大を行う事で別の体である「拡大体」という集合ができると解釈します。逆に、拡大した体の側から見た時、もとの体は「部分体」であると言います。
より一般的には、2つの体KとLがあるとしてLがKの拡大体である時、その「拡大」自体の事を記号でL/Kと書きます。この表記を使うと、例えば実数から複素数への拡大は\(\mathbb{C}\)/\(\mathbb{R}\)と表されるわけです。
もちろんこの記号は、対象のKとLが体である時に限って体の拡大としての意味を持ちます。
【通常の数や関数についてはx/yは割り算で、対象が群ならG/Hは剰余群、環であれば剰余環、特に指定のない集合に対しては差集合を表します。】
体の「拡大」
- \(\mathbb{C}\)は\(\mathbb{R}\)の「拡大体」
- \(\mathbb{R}\)は\(\mathbb{C}\)の「部分体」
- 記号では、実数体→複素数体への「拡大」を
\(\mathbb{C}\)/\(\mathbb{R}\)
と書く。
複素数に関しては複素関数論などでも詳しく扱われるので、ここでは有理数に対するp+q\(\sqrt{2}\)の形の数を元に持つ集合\(\mathbb{Q}\left(\sqrt{2}\right)\)などについて具体例として詳しく見てみます。
平方根の計算を行う時、例えば$$(1+2\sqrt{2}+\sqrt{3})+(2-\sqrt{2}+3\sqrt{3})$$ $$=(1+2)+(2-1)\sqrt{2}+(3+1)\sqrt{3}$$ $$=3+\sqrt{2}+4\sqrt{3} $$のように、「有理数だけの項」「2の平方根の項」「3の平方根の項」ごとに分けて加算や減算を行います。平方根でなくても3乗根でも4乗根でもよく、要するに無理数があれば同じように計算します。
このような時、有理数全体\(\mathbb{Q}\)の元に対して、何か有理数でない別の元を組み合わせて計算を行っているわけです。2+3\(\sqrt{2}\) のような数は「実数」の元であると言うのはもちろん正しい表現ですが、この形の元に限ったものだけを集めて「体」の構造を保つようにしたものは有理数の「拡大体」と見なすことができ、\(\mathbb{Q}\left(\sqrt{2}\right)\) のように書きます。実数に対する複素数と同様に考えるという事です。
$$\mathbb{Q}(\sqrt{2})=\{p+q\sqrt{2}|p,q\in\mathbb{Q}\}$$
このようなものを考える時は、3の平方根などの他の無理数は考えずにp+q\(\sqrt{2}\) の形の数同士の加減乗除の計算を考えます。この時、q=0とすれば通常の有理数になるので、集合として、\(\mathbb{Q}\subset\mathbb{Q}\left(\sqrt{2}\right)\) のような包含関係になります。2の平方根を添加した拡大体のほうが、もとの有理数全体よりも大きい集合です。
この場合の加減乗除の計算自体は通常の平方根を含む計算と全く同じですが、複素数の計算との類似性に注意すると共通点が見えてくるかと思います。
$$(p_1 +q_1\sqrt{2})\pm (p_2 +q_2\sqrt{2})=(p_1\pm p_2)+(q_1\pm q_2)\sqrt{2}\in\mathbb{Q}\left(\sqrt{2}\right)$$
$$(p_1 +q_1\sqrt{2})(p_2 +q_2\sqrt{2})=(p_1p_2+2q_1q_2)+(p_1q_2+p_2q_1)\sqrt{2}\in\mathbb{Q}\left(\sqrt{2}\right)$$
$$\frac{1}{p +q\sqrt{2}}=\frac{p -q\sqrt{2}}{(p +q\sqrt{2})(p -q\sqrt{2})}=\frac{p -q\sqrt{2}}{p^2 -2q^2}\in\mathbb{Q}\left(\sqrt{2}\right)$$
商のところに関しては、1を割ったものだけ考えれば一般の商はそれとの積と考えられるので分子を1としています。このように、加減乗除の計算の計算結果後も\(\mathbb{Q}\left(\sqrt{2}\right)\)の集合に属するので、このような時に体\(\mathbb{Q}\left(\sqrt{2}\right)\)は加減乗除の計算に関して「閉じている」と言います。
\(\mathbb{Q}\left(\sqrt{3}\right)\) や \(\mathbb{Q}\left(\sqrt{5}\right)\)のような拡大体でも事情は同じで、加減乗除の計算に関して閉じています。
ここで、p+q\(\sqrt{2}\) +r\(\sqrt{3}\) のような形の場合には拡大体として見る場合には注意が必要で、記号としては\(\mathbb{Q}\left(\sqrt{2},\sqrt{3}\right)\) のように書きますが、実際のところは \(\sqrt{6}\) も含まれます。これは、積や商の計算で\(\sqrt{2}×\sqrt{3}=\sqrt{6}\) が発生するためです。つまり実質的には、この拡大体は次のような形をしています。
$$\mathbb{Q}\left(\sqrt{2},\sqrt{3}\right)=\{p+q\sqrt{2}+r\sqrt{3}+s\sqrt{6}|p,q,r,s\in\mathbb{Q}\}$$
$$例えば、1+3\sqrt{2}+\frac{\sqrt{3}}{2}+2\sqrt{6}\in \mathbb{Q}\left(\sqrt{2},\sqrt{3}\right)$$
この場合、(\(\sqrt{6}\))2=6、\(\sqrt{2}×\sqrt{6}=2\sqrt{3}\)、\(\sqrt{3}×\sqrt{6}=3\sqrt{2}\) となるので2、3,6以外の平方根は加減乗除の計算で発生しません。
同じような注意点は、3乗根による有理数体の拡大を考える時にも発生します。
一見違うように見える拡大体が、実際は同一の集合である場合もあります。
\(\mathbb{Q}\left(\sqrt{2},\sqrt{3}\right)\) と少し似た\(\mathbb{Q}\left(\sqrt{2}+\sqrt{3}\right)\) という拡大を考えると、一見別の体になる?ようにも見えますが、
じつは\(\mathbb{Q}\left(\sqrt{2},\sqrt{3}\right)\)=\(\mathbb{Q}\left(\sqrt{2}+\sqrt{3}\right)\)です。
$$p+q(\sqrt{2}+\sqrt{3})$$
$$(\sqrt{2}+\sqrt{3})^2=5+2\sqrt{6},(\sqrt{2}+\sqrt{3})^3=2\sqrt{2}+6\sqrt
{3}+9\sqrt{2}+3\sqrt{3}=11\sqrt{2}+9\sqrt{3}$$
2乗のほうの形に注目すると、まず\(\sqrt{6}\)単独を\(\left(\sqrt{2}+\sqrt{3}\right)\)で表す事ができ、
3乗のほうの形に注目すると\(\sqrt{2}\)や\(\sqrt{3}\)単独を、\(\left(\sqrt{2}+\sqrt{3}\right)\)の加減乗除で表せます。
$$(\sqrt{2}+\sqrt{3})^3-9(\sqrt{2}+\sqrt{3})=2\sqrt{2},\hspace{15pt}(\sqrt{2}+\sqrt{3})^3-11(\sqrt{2}+\sqrt{3})=-2\sqrt{3}$$
$$p+q\sqrt{2}+r\sqrt{3}+s\sqrt{6}=p+q\frac{(\sqrt{2}+\sqrt{3})^3-9(\sqrt{2}+\sqrt{3})}{2}-r\frac{(\sqrt{2}+\sqrt{3})^3-11(\sqrt{2}+\sqrt{3})}{3}+\sqrt{6}$$
$$=p-\frac{5}{2}+\left(\frac{11r}{3}-\frac{9q}{2}\right)(\sqrt{2}+\sqrt{3})+\frac{s}{2}(\sqrt{2}+\sqrt{3})^2+\left(\frac{q}{2}-\frac{r}{3}\right)(\sqrt{2}+\sqrt{3})^3$$
\(\left(\sqrt{2}+\sqrt{3}\right)\)を4乗すると再び2、3,6の平方根が出てくるので4以上のベキ乗を考える必要はなく、有理数全体を動く独立変数が4つありますので、少々汚い形ですがこれは\(\mathbb{Q}\left(\sqrt{2}+\sqrt{3}\right)\)と同じ集合になります。
この例はちょっとめんどくさい計算でしたが、より簡単な例では実数体→複素数体の拡大の中にも見られます。実数を複素数に拡大する時はi2=-1となるiを考えました。では、\(\alpha\)3=-1となるような「別の実数で無い数?」を考えると別の拡大が可能でしょうか?
じつのところ、\(\alpha\)3=-1となる\(\alpha\)は、複素数で表せてしまいます。理屈は簡単で、ドモアブルの定理を使えばcos(\(\pi\)/3)+isin(\(\pi\)/3), cos(2\(\pi\)/3)+isin(2\(\pi\)/3), -1の3つが該当します。(よく考えてみると当然ですが、これらの1つは実数です。)同様に、\(\alpha\)n=-1を満たす\(\alpha\)を使って実数体の拡大を考えても、全て集合としては「複素数」と同じになってしまうわけです。
【ただし、それらの拡大を実数体ではなく有理数体の拡大として考えると話は変わってきます。】
では、実数については複素数以外の拡大はあり得ないのかというと、結論は「あります」。例えば複素数体の拡大として「四元数体」と呼ばれるものが該当します。さらに八元数と呼ばれるものを考える事も可能ですが、これは積の結合法則が成立しないものなので「体」には含まれません。
多項方程式の解による体の拡大【用語の整理】
体論の基本的な理論の中で重要な拡大の1つは、多項方程式の解による拡大です。キーワードはいくつかあるので整理しましょう。1つ1つの意味は大した事ないのですが、これらをごちゃごちゃに文章の中で使われると結構混乱する人も多いと思います。
■ 「既約」 ■ 「モニック」 ■ 「体上の多項式」 ■ 「最小多項式」 ■ 「共役」
「既約」
多項式が既約であるとは、簡単に言うとそれ以上「因数分解できない」という意味です。
これは「どの体で考えているか」によってどの式が既約かそうでないかが変わってくる事に注意が必要です。
例えば、x2-2は、実数の範囲では因数分解可能ですが、有理数に限定した場合はそうではありません。そのためこの式は「有理数体上で既約である」あるいは「\(\mathbb{Q}\)上で既約である」と、代数学では表現します。
同様に、x2+2は複素数の範囲では因数分解可能ですが実数の範囲では因数分解できないので、「\(\mathbb{R}\)上で既約」であり、\(\mathbb{C}\)上では既約ではないと表現します。
「モニック」
「モニック」とは、多項式の最大の次数(ベキ乗の数)の項の係数が1であるという事です。
これは、意味自体は簡単な事で、大げさな事ではありません。
【「モノ」とは単一とか1を表す語で「モノクロ」とか「モノラル」等の「モノ」です。】
x2-2x+1, x3+x, x+1, x4+3x2+2などの多項式はみな「モニック」です。
2x2-2x+1, 3x+1, -x4+3x2+2などの多項式はモニックではありません。
「体上の多項式」
係数は全て体Kの元である多項式を「K上の多項式」と言います。
例えば、x2-2x+1などの実数係数の多項式は「\(\mathbb{R}\)上の多項式」の1つです。x2-2ix+1などは、実数で表せないiが係数に入っていますので「\(\mathbb{C}\)上の多項式」(のうち\(\mathbb{R}\)上の多項式を含まないもの)の1つです。
「最小多項式」
\(\alpha\)∊Lと、ある体KがあってK上の多項式でf(\(\alpha\))=0となるもののうち「既約」で「モニック」で「次数が最小のもの」を特に「最小多項式」と言います。
例えば、x2+1はi∊\(\mathbb{C}\)の\(\mathbb{R}\)上の最小多項式です。
x2-2は\(\sqrt{2}\)∊\(\mathbb{R}\)の\(\mathbb{Q}\)上の最小多項式です。
ここで、もし\(\sqrt{2}\)∊\(\mathbb{R}\)に対して\(\mathbb{R}\)上の最小多項式を考えるなら、それは1次式x-\(\sqrt{2}\)になります。
ちょっと整理すると次のようになります。
「\(\alpha\)∊LのK上の『最小多項式』」とは:LはKの拡大体であるとして、
体Kの元を係数とする多項式、つまり「K上の多項式」のうち、
次のものを\(\alpha\)∊LのK上の最小多項式と言います。
- \(\alpha\)∊Lを代入すると0になる【f(\(\alpha\))=0となる】
- そのうち次数(xnのn)が最小のもの
- 既約である
- モニックである
具体的な数に対する最小多項式を導出する時には計算の工夫が必要な場合もあります。
例えば \(\alpha=\sqrt{2}+\sqrt{3}\) の「\(\mathbb{Q}\)上の最小多項式」が具体的にどんなものかを知りたい場合には、
まず式を変形してから \(\alpha -\sqrt{2}=\sqrt{3}\) の両辺を2乗します。$$\alpha^2-2\sqrt{2}\alpha+2=3$$$$\Leftrightarrow \alpha^2-1=2\sqrt{2}\alpha$$2乗した後にさらに変形した後の式の両辺を、さらに2乗します。$$\alpha^4-2\alpha^2+1=8\alpha^2\Leftrightarrow \alpha^4-10\alpha^2+1=0$$
このように、2段階に分けて平方根の部分を有理数にしています。
\(\alpha=\sqrt{2}+\sqrt{3}の\mathbb{Q}\)上の最小多項式はx4-10x2+1です。【係数は確かに有理数。】
「共役」
複素数で「共役複素数」というものがありますが、これはより一般的に言うと、L上のある元\(\alpha\)に対するK上の最小多項式f(x)に対して、\(\alpha\)以外でf(x)の根になる【f(x)=0の解になる】\(\alpha\)以外の他のLの元の事を指します。
複素数で言うと、1+iの共役複素数1-iはともにx2+2x+2=0の解ですが、この左辺の多項式は「1+iの\(\mathbb{R}\)上の最小多項式」です。1-iは1+iの「\(\mathbb{R}\)上の共役」であると言います。
この意味では、共役というものは1つだけではなくもっと多くある事もあり得ます。x3-2は3\(\sqrt{2}\)∊\(\mathbb{R}\)の\(\mathbb{Q}\)上の最小多項式ですが、3\(\sqrt{2}\)∊\(\mathbb{C}\)と考えると、x3-2=0を満たす別の2解が存在します。それらが3\(\sqrt{2}\)∊\(\mathbb{C}\)の\(\mathbb{Q}\)上の共役になります。
「代数拡大」
変数は複素数範囲、係数は実数である多項方程式(\(\mathbb{R}\)上の多項式)があったとしましょう。
【上記の通り、係数が全て体Kの元である多項式が「K上の多項式」です。】
任意の複素数xに対して、そのxが解となる実数係数の多項式は存在し、
そのような時に実数から複素数への拡大\(\mathbb{C}\) /\(\mathbb{R}\)は「代数拡大」と呼ばれます。
例えばてきとうな実数係数の多項式 x4+x3+\(\sqrt{2}\)x2-x+1=0 などを考えると、
これを満たすx∊\(\mathbb{C}\)は必ず存在します【代数学の基本定理】。
現にこの多項方程式の解となるx=\(\alpha\) に対して、「\(\alpha\)∊\(\mathbb{C}\)は \(\mathbb{R}\) 上『代数的』である」という表現をします。
この「代数的」という語を使う時には、必ずL/Kという拡大があって、
「拡大体Lのほうの元」に対して、「K上」代数的であると言います。
これを一般の体K、Lについて置き換えると、\(\alpha\)∊Lに対して係数a1~an∊Kが存在して
\(\alpha\)n+a1\(\alpha\)n-1+・・・+an-1\(\alpha\)+an=0となる時、\(\alpha\)∊L はK上で「代数的である」と言い、
任意のx∊LについてxがK上代数的である時、KからLへの拡大L/Kは「代数拡大」であると言います。
任意のx∊Lについて表現する用語なので、L/Kは「K上の代数拡大」という具合に言えばよい事になります。\(\mathbb{C}\)/\(\mathbb{R}\)は「\(\mathbb{R}\)上の代数拡大」である(単に拡大である事に加えて)という表現の仕方になります。
特に、K上の任意の多項式f(x)に対してf(\(\alpha\))=0となるような\(\alpha\)∊Kが存在する時、
Kは「代数閉体」であると言います。複素数体は代数閉体であり、実数体や有理数体は代数閉体ではありません。【例えばf(x)=x2+1などを考えれば、これをゼロにするxはx=+i,-iなので。】
ここで、体の拡大L/Kがあって拡大体Lのほうが代数閉体である時には「LはKの『代数閉包』である」と言います。
この手の数学の分野は、上記のように様々な用語が出てきてややこしい事は間違いないのですが、意味や具体例を考えながら整理していくと意外と面白いかもしれない分野です。