アンペールの法則は電流と磁場の関係を表す式であり、マクスウェル方程式の1つです。マクスウェル方程式の他の3式のように積分形と微分形の両方があり、数式的には微分形は磁場の回転(rot)で含む形をしています。また、時間変動(時間による偏微分)の観点からは電場の時間変動を含む式です。
この記事では、他の電磁場の法則や数学の定理との関係を中心にアンペールの法則の内容と性質について整理してまとめています。
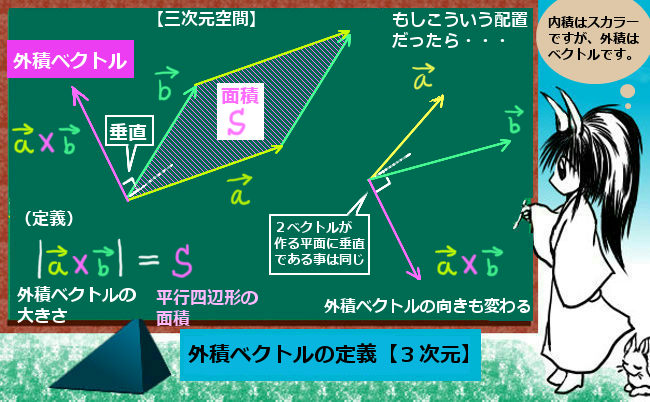
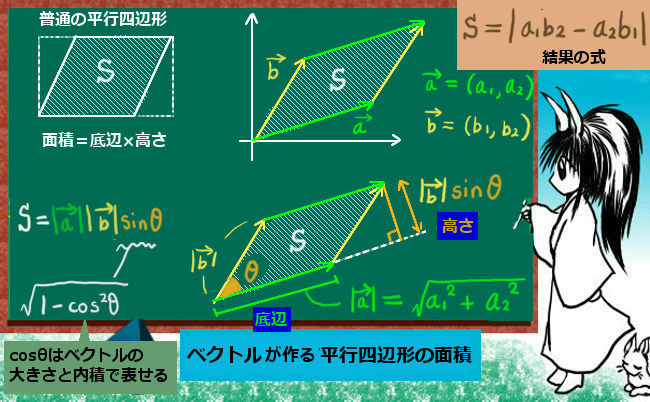
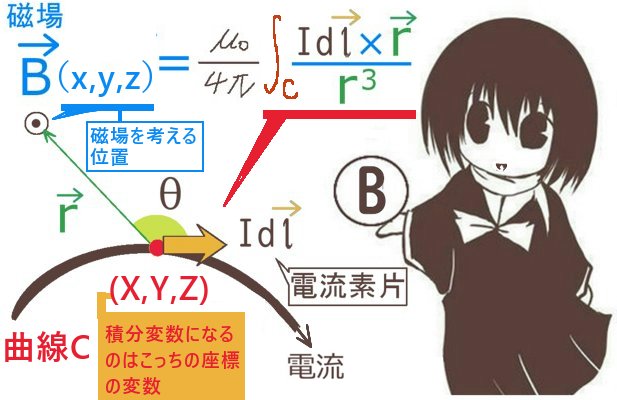
アンペールの法則は、いくつかの条件のもとでビオ・サバールの法則と等価である事が知られています。アンペールの法則は磁場の循環(周回の接線線積分)および磁場の回転と、電流・電流密度・変位電流との関係を表す式ですが、ビオ・サバールの法則は電流または電流密度からベクトル場としての磁場を直接表す形をした法則です。
法則の内容
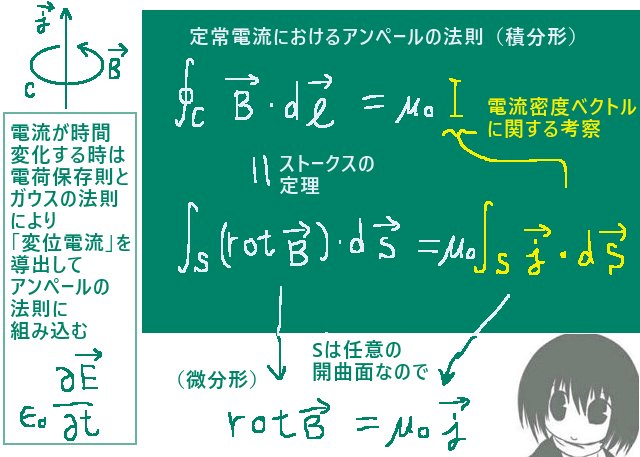
アンペールの法則の積分形は基本的には磁場の接線線積分(ここでは周回積分であり、循環とも言う)で書かれて、それはストークスの定理によって磁場の回転の法線面積分でも書ける事になります。それに関連して、アンペールの法則の微分形は数式的には磁場の回転を表す式です。
アンペールの法則における閉曲線Cと開曲面S(閉曲面では無く)の関係は、ある閉曲線Cがあった時にそれを外縁(外周)に持つ「任意の開曲線S」になります。つまり閉曲線Cのところで切れて開曲面になっている事を条件に、曲面Sは形状を問わないという事です。ですから1つのCに対してS1とかS2とかのたくさんの開曲面があり得ます。ただしここでは、左辺と右辺の両方に法線面積分の項がある時は積分領域の曲面Sは両辺で同じものを指しています。
以下、\(\overrightarrow{B}\)は磁場、\(\overrightarrow{E}\)は電場、\(\overrightarrow{j}\)は電流密度、\(I\)は電流の大きさ\(\left(=\left|\overrightarrow{j}\right|\right)\)です。
■一般の形
$$\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\mu_0\int_S\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)\cdot d\overrightarrow{s}$$
■特に電場の時間変化が無い時
(これは電流の時間変化が無い時でもあります。)
$$\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\mu_0\int_S\overrightarrow{j}\cdot d\overrightarrow{s}=\mu_0I$$
これらの式はいずれもストークスの定理を使って、
左辺(周回積分の項)を変形して次のようにも書けます。
$$一般の形\hspace{3pt}\int_S\left(\mathrm{rot}\overrightarrow{B}\right)\cdot d\overrightarrow{s}=\mu_0\int_S\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)\cdot d\overrightarrow{s}$$
$$\frac{\partial\overrightarrow{E}}{\partial t}=0の時、\int_S\left(\mathrm{rot}\overrightarrow{B}\right)\cdot d\overrightarrow{s} =\mu_0\int_S\overrightarrow{j}\cdot d\overrightarrow{s}=\mu_0I$$
電場\(\overrightarrow{E}\)の時間微分の項\(\Large\epsilon_0{\frac{\partial\overrightarrow{E}}{\partial t}}\)は変位電流と呼ばれますが、
それは導線に生じている電荷の流れとしての「電流」とは別物なので注意も必要です。
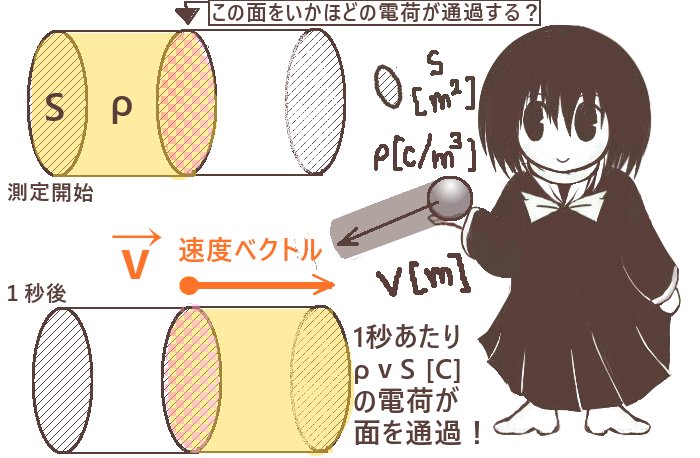
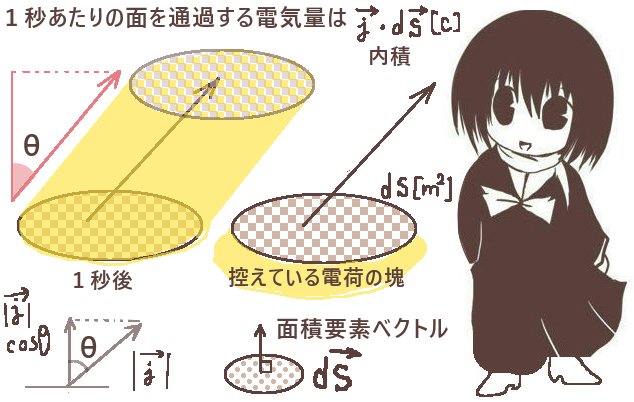
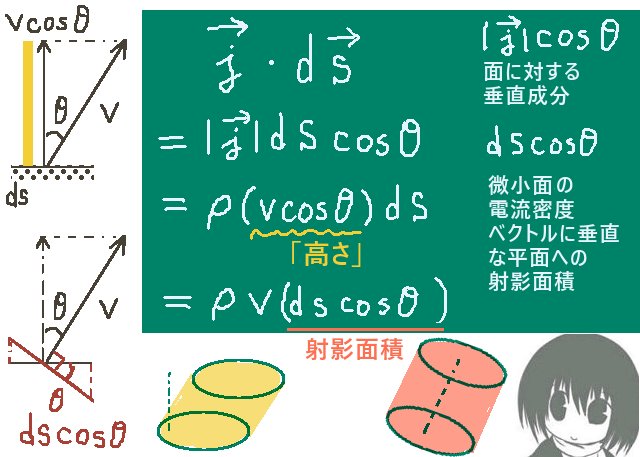
電流に相当するのは、電流を向き付きで単位面積あたりで表した電流密度\(\overrightarrow{j}\)のほうです。
ただし後述するように変位電流とは電荷保存則に由来する量でもあり、具体例によっては電流との関係も確かに深い事が伺えます。
ストークスの定理によって法線面積分で表した形の式を見ると、左辺と右辺がともに法線面積分となっています。先ほど触れたように積分領域の曲面Sは閉曲線Cを外縁とする条件のもとで任意の形状なので、式が成立するには積分の中身が一致していないといけません。そしてそれがアンペールの法則の微分形になります。
◆一般の形 $$\mathrm{rot}\overrightarrow{B}=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)$$ ◆電場の時間変化が無い時または電流の時 $$\mathrm{rot}\overrightarrow{B}=\mu_0\overrightarrow{j}$$
これらをナブラを使って書くなら次のようになります。
アンペールの法則には、多くの式にベクトル場の 「回転」が含まれている事が分かります。そこで回転を「∇×」の記号で書いた場合は次のようになります。 $$\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\int_S\left(\nabla\times\overrightarrow{B}\right)\cdot d\overrightarrow{s}=\mu_0\int_S\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)\cdot d\overrightarrow{s}=\mu_0I$$ ◆電場の時間変化が無い時または電流の時 $$\nabla\times\overrightarrow{B}=\mu_0\overrightarrow{j}$$

定電流の時のアンペールの法則の修正版として一般形を考える場合
アンペールの法則は、基本的に電流が作る磁場の回転についての関係式です。実際、実験から元々分かっていた事は電流がその周囲に環状の磁場を作るという事でした。
上記の一般形の式を見てもらえば分かるように、定常電流(=時間変化が無い電流)の時のほうがもちろん式が簡単で使いやすいものになります。
そのため、電流が作る静磁場を考える時には普通は定常電流の時の形を指してアンペールの法則と呼んでいるわけです。
しかし定常電流である時の式を、時間変動がある場合にそのまま当てはめると理論的に見ておかしいという事が発生します。
そのため、時間変動がある場合も含めたアンペールの法則は定常電流の場合の法則の式を「修正」したものであるとよく表現されます。
❖定電流の時の積分形(循環と法線戦面積分の2つの形式) $$\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\mu_0I$$ $$\int_S\left(\mathrm{rot}\overrightarrow{B}\right)\cdot d\overrightarrow{s} =\mu_0I$$ ❖定電流の時の微分形(一般の場合と同じ導出方法) $$\mathrm{rot}\overrightarrow{B}=\mu_0\overrightarrow{j}$$
ベクトル場(磁場に限らず)に対しては次の関係式が数学的に成立します。 $$\oint_C\overrightarrow{F}\cdot d\overrightarrow{l}=\int_S\left(\mathrm{rot}\overrightarrow{F}\right)\cdot d\overrightarrow{s}$$
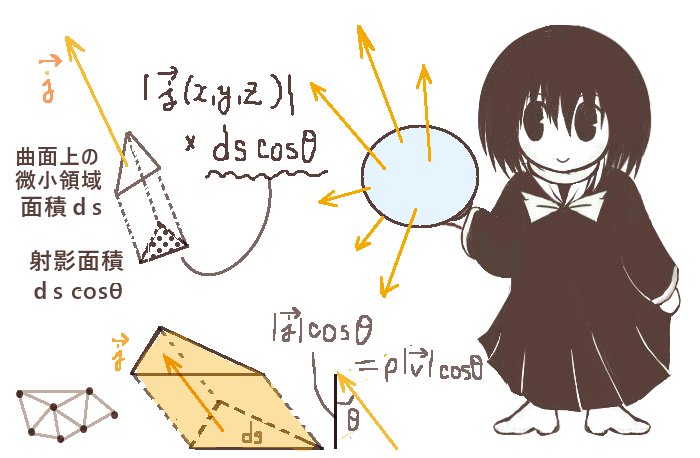
$$I=\int_S\overrightarrow{j}\cdot d\overrightarrow{s}$$ この関係式は電流密度ベクトルと電流の定義に深くかかわっています。
この時、微分形のほうの発散を考えると
$$\mathrm{div}\left(\mathrm{rot}\overrightarrow{B}\right)=0\hspace{5pt}なので\hspace{5pt}\mathrm{div}\overrightarrow{j}=0$$
他方、電荷保存則の微分形に対する発散を考えて、さらに電場に関するガウスの法則の微分形を適用すると次式です。
$$\mathrm{div}\overrightarrow{j}=-\frac{\partial \rho}{\partial t}=\frac{\partial}{\partial t}\left(\epsilon_0\mathrm{div}\overrightarrow{E}\right)=\mathrm{div}\left(-\epsilon_0\frac{\partial}{\partial t}\mathrm{div}\overrightarrow{E}\right)$$
$$\Leftrightarrow\mathrm{div}\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)=0$$
この発散を全体で考えた時の第2項の\(\Large\epsilon_0{\frac{\partial\overrightarrow{E}}{\partial t}}\)を「変位電流」と呼ぶわけですが、話を整理するとこれは電荷保存則から出てきた量です。そのため、この時点ではアンペールの法則に無関係に考える事ができる量であると言えます。
変位電流とは次の式で表される量です。 $$\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}$$
- 電荷保存則という基本前提が成立する限りにおいて、
変位電流は「電荷密度の時間変化」に由来する量として必ず考える事ができる。 - 変位電流に対して成立する関係式は、発散に対して成立する次式。
$$\mathrm{div}\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)=0$$
微分形
$$\mathrm{div}\overrightarrow{j}=-\frac{\partial \rho}{\partial t}$$
電荷密度の時間変化率が0の時(=電流の時間変化率が0)
$$\mathrm{div}\overrightarrow{j}=0$$
電流を電荷の流れと考えた時に基本前提として積分形が存在すると考えて、
ガウスの発散定理を適用すると微分形を導出できます。積分形は次の通りです。
$$
\int_S\overrightarrow{j}\cdot d\overrightarrow{s}=-\int_V\frac{\partial \rho}{\partial t}dv\left(=-\frac{\partial }{\partial t}\int_V\rho dv\right)
$$
(ここでのSとVは「閉曲面」およびその内部の領域です。)
$$\mathrm{div}\overrightarrow{E}=\frac{\rho}{\epsilon_0}\hspace{5pt}\Leftrightarrow\hspace{5pt}\rho=\epsilon_0\mathrm{div}\overrightarrow{E}$$ ρは電荷密度です。
他方で「磁場の回転」の発散は0(これは数学的にベクトル場であれば何でも瀬成立)なので、定常電流におけるアンペールの法則によればそれは電流密度の定数倍です。
ところで電流が定常電流では無い時でも、磁場の回転自体は発散をとると数学的に0になるわけですから、\(\mathrm{rot}\overrightarrow{B}\)を電流に関係する何かで表すとすると、とりあえず「アンペールの法則とは無関係に成立している」\(\mathrm{div}\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)=0\) の関係式は、いかにも関係がありそうであるというわけです。
そこで、定常電流の場合のアンペールの法則の電流側の項に変位電流も加わるとすれば、定常電流の時は「電荷密度の時間変化が無い⇒変位電流は0」なので元々の形の式はそのまま使えて、電流の時間変化がある時は発散を考えた時にも整合性がとれる式ができます。しかもてきとうな項を付け加えたというのではなく、電荷保存則に由来する関係式を使っています。
それで、その形を定常電流の時のアンペールの法則を「修正」したものとして、変位電流の項を加えたものが一般の場合のアンペールの法則の式の形であると考えられているわけです。
- \(\mathrm{div}\left(\mathrm{rot}\overrightarrow{B}\right)=0\) は電流の時間変化のある無しに関わらず数学的に成立
- \(\mathrm{div}\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)=0\) も電流の時間変化のある無しに関わらず成立(電荷保存則より)
- 電流の時間変化が無い場合、
電荷保存則由来の式では変位電流の項が0で
\(\mathrm{div}\overrightarrow{j}=0\) - 電流の時間変化が無い場合、定常電流に対するアンペールの法則により
\(\mathrm{rot}\overrightarrow{B}=\mu_0\overrightarrow{j}\)であるので
\(\mathrm{div}\overrightarrow{j}=0\)(これは電流の時間変動がある場合には電荷保存則により成立しない。) - そこでもし、
\(\mathrm{rot}\overrightarrow{B}=\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)\)だとしても
電流の時間変化があるか無いかに関わらず
左辺の発散は数学的に0、
右辺の発散は電荷保存則により0なので、 「矛盾が生じない」式になります。
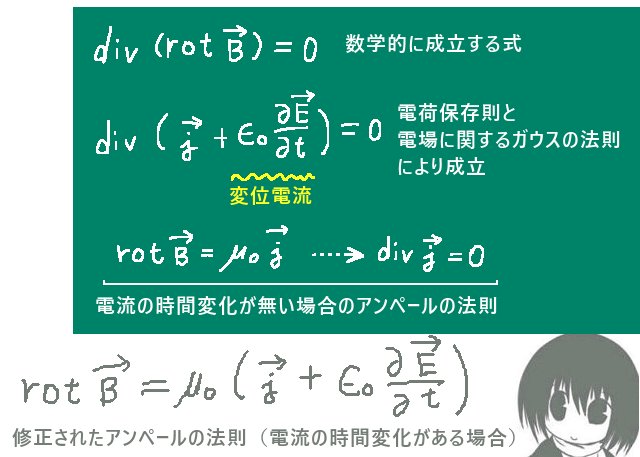
そのため、アンペールの法則の微分形の一般形を変位電流を加えた形で考える事にすると、定常電流の時の法則の積分形から微分形を導出した時の逆算で磁場の法線面積分を書くと積分形のほうの一般形になります。
$$\int_S\left(\mathrm{rot}\overrightarrow{B}\right)\cdot d\overrightarrow{s}=\mu_0\int_S\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)\cdot d\overrightarrow{s}$$
$$ストークスの定理により\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\int_S\left(\mathrm{rot}\overrightarrow{B}\right)\cdot d\overrightarrow{s}なので$$
$$\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\mu_0\int_S\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)\cdot d\overrightarrow{s}$$
ストークスの定理を使っていますので、この時にSは開曲面であるとして閉曲線Cを外縁に持つものとします。アンペールの法則の一般形がまずあると考えてそこから微分形を導出する時と同じです。
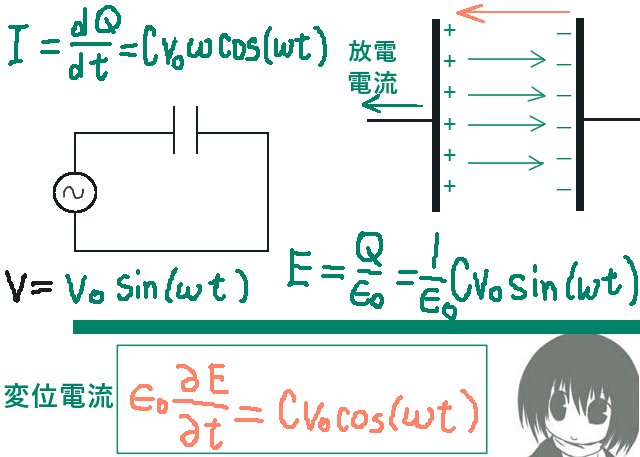
コンデンサーにおける変位電流
前述の通り、定常電流におけるアンペールの法則に付け加わる「変位電流」自体は、電荷保存則の成立を前提とする限りはアンペールの法則とは無関係に量として想定できる性質のものです。
そこで、ここでは変位電流とは電荷の流れとしての電流そのものではないけれども「確かに物理的な意味を持つ量である」という事をより明確にするために、交流回路におけるコンデンサーの極板間の電場の時間変化(その1/ε0倍が変位電流)を例に考えてみます。
電気回路におけるコンデンサーに電圧をかけると、
極板には電圧(=電位差)に比例する量で電荷がたまり、極板間には電場が生じます。直流電気回路では導線に短時間だけ充電電流・放電電流が発生し、交流電気回路ではそれが短い周期で繰り返されて導線中に常に交流電流が発生します。
1つの極板上の極板間の電圧をV、電荷をQとすると、Q=CVの比例関係があります。
交流回路で V=CV0sin(ωt)とするとQ=CV0sin(ωt)
【Cは比例定数で、電気容量とかキャパシタンスなどと呼ばれます。】
また、極板間距離が十分距離が小さくて電場の方向がほぼ一定とみなせるとすると、
電場に関するガウスの法則を使って
「電場の大きさEは極板間におけるどの位置でも同じである」と考える事ができます。
(コンデンサーにおいて電場は極板間で「一様である」とも表現されます。)
さらに同じく電場に関するガウスの法則によれば、
その電場の大きさは極板の表面にする分布する電荷の1/ε0倍の電気量に等しい事になります。
すると、E=Q/ε0=(CV0/ε0)sin(ωt)です。
【ガウスの法則は時間変化がある場合でも1つ1つの任意の時刻で考える限り成立します。】
「コンデンサーの極板間において電場は一様である」という事
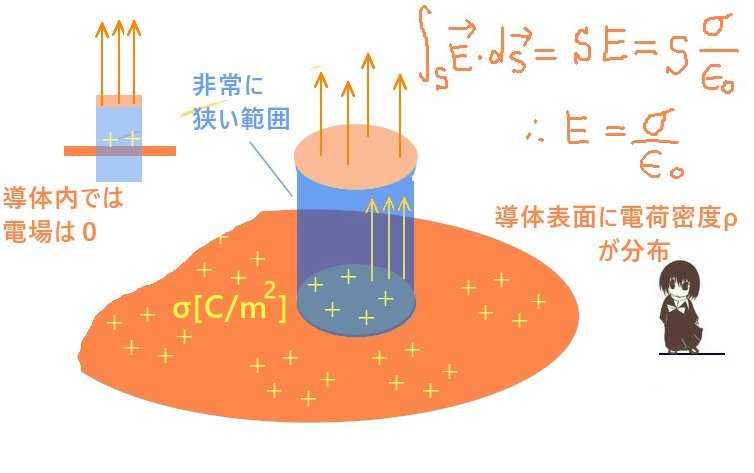
2枚の極板同士の間隔が十分小さいコンデンサーについて、「無限に広い導体平板」に近似できると考える事で「表面上に一様に分布した電荷が表面から近い位置に作る電場」を計算します。
電荷は表面に1m2あたりσ [C]で分布するとします。一般的に導体の内部では電場が0であると考えられ、表面から近い場所で電場の方向は合成されて表面に垂直である事に注意します。閉曲面として平板に垂直な底面積Sの柱体を考えた時に(円柱でも直方体でも何でも可)電場に関するガウスの法則において法線面積分が0にならないのは平板に平行で導体外部にある1つの面だけです。
電場はそれに垂直なのでE S=σS/ε0 ⇔ E=σ/ε0 つまり、少し妙に思えるかもしれませんが電場の大きさは「平板からの距離に依存しない」という事になります。コンデンサーにおいても極板間の距離が十分小さければ同じ状況に近似できるとする事が「極板間で電場は一様である」と考える理論的な根拠の1つです。
【尚、これがもし平板ではなく直線状の棒であったら、それが無限に長いとみなせても軸の周りに同じ大きさの電場が同心円に垂直な形でできるので、無限に広い平板の時と同じような結果にはなりません。クーロン力から積分で直接計算してもガウスの法則を使っても、電場の大きさは棒からの距離に反比例するという結果を得ます。】
ところでこの場合での「変位電流」については、まず向きが一定である事から大きさだけを考えます。
そして変数は時間tだけである事も考慮すると、変位電流の大きさは次のようになります。
ε0(dE/dt)=ε0(CV0/ε0)sin(ωt)=CV0cos(ωt)
他方で、電気回路における電流は実測できるものでもありますが、コンデンサーの極板に出入りする電流を理論的にはどのように考えるかというと、実は「電荷の流れ」を電荷の時間変化と考えて、
dQ/dtとして表すのです。すると、Q=CV0sin(ωt)でしたので極板に出入りする電流は、
I=dQ/dt=CV0cos(ωt)
という事は、ε0(dE/dt)=I=CV0cos(ωt)となり(※)、
コンデンサーを含む部分については「導線中の電流」と「極板間(絶縁部分)の変位電流」が全く同じ値で計算できる事を意味します。つまり、交流電気回路の平板コンデンサーという特別な場合である事を強調しておく必要はありますが「通常の電流と変位電流とで実質的に1つの閉回路が作られ、各時刻で同じ値として表せる」という物理的な意味を変位電流が持つ例となっています。
(※)ここでの計算は、変位電流とε0(dE/dt)と交流電流Iが結果としては「この条件下では同じ値で表せる」という事であって、一般的には同じものではないので注意も必要です。物理的に見ても、極板間には電流は生じておらず表面を除いて電荷も存在しない(つまりQ=0)から電場の時間変化を代わりに考えたわけであって、ε0(dE/dt)とI=dQ/dtを一般的に同じ量であるとはみなせません。電荷保存則を考えてみても、電流密度と変位電流の間に所定の関係式は常に成り立つけれども「同じ物理量ではない」わけです。
変位電流と磁場の関係(マクスウェル方程式での意味)
ところで、変位電流をアンペールの法則に組み込む事に関しては確かに数式的な強い関連性は伺えるものの、他の法則と比較すると少々無理やり感もあると言えるかもしれません。
疑問が残るとすれば、やはり「変位電流が、通常の電流と同じように磁場を発生させるのか」という点ではないでしょうか。前述のコンデンサーの例においても、確かに変位電流と通常の電流の数式上の強い関連性について示すものではありますが発生する磁場については何も分かるものではありません。
実の所、単独の変位電流を実験で扱う事はなかなか難しいようで少々うやむやにされている面もあると言えます。「通常の電流を完全に抜きにして、変位電流だけでアンペールの法則が記述する磁場は本当に発生するのか」という問いの解答をはっきりと実測結果で示す研究はあまり多くないようです。
ただし、間接的には変位電流を含んだアンペールの法則の一般的な形が法則として正しい事を示す実験結果は既に存在します。それが電磁波の存在と、その応用および実用です。
マクスウェル方程式から電磁波の定量的な関係式を導出する時には、実はアンペールの法則において変位電流の項がないと上手くいきません。
ここでは簡単にだけ述べますが、アンペールの法則の微分形に対してさらに回転を考えて、電磁誘導の式の微分形を代入する事で電場を含まない形に変形できます。
$$\mathrm{rot}\left(\mathrm{rot}\overrightarrow{B}\right)=\mathrm{rot}\left\{\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)\right\}$$
$$電磁誘導の式の微分形\mathrm{rot}\overrightarrow{E}=-\frac{\partial \overrightarrow{B}}{\partial t}を代入して整理すると、$$
$$\mathrm{rot}\left(\mathrm{rot}\overrightarrow{B}\right)=\mu_0\mathrm{rot}\overrightarrow{j}-\epsilon_0\mu_0\frac{\partial^2\overrightarrow{B}}{\partial t^2}$$
ここでの式をナブラ記号を使って書いた場合は次の通りです。
どっちの方法が見やすいかは人によって違うと思います。
$$\nabla\times\left(\nabla\times\overrightarrow{B}\right)=\nabla\times\left\{\mu_0\left(\overrightarrow{j}+\epsilon_0\frac{\partial\overrightarrow{E}}{\partial t}\right)\right\}$$
$$\nabla\times\overrightarrow{E}=\frac{\partial \overrightarrow{B}}{\partial t}により、$$
$$\nabla\times\left(\nabla\times\overrightarrow{B}\right)=\mu_0\nabla\times\overrightarrow{j}-\epsilon_0\mu_0\frac{\partial^2\overrightarrow{B}}{\partial t^2}
$$
計算の続きとしては、今度は左辺のほうを回転に対して成立する式で置き換えて磁場に演算子が作用する形の微分方程式を作ります。
これに相当する式をベクトルポテンシャルで表す方法もありますが、その場合もやはりアンペールの法則の一般形の式は必要です。
アンペールの法則の微分形における「磁場の回転」に対してさらにもう1回「回転」を作用させる式は、実は定常電流が作る静磁場においてベクトルポテンシャルを考える時にも使う式です。
ただし、その場合は変位電流の項が0であると考えますから右辺は電流密度ベクトルだけを考えます。
また、電磁波を導出するためにベクトルポテンシャルを考える時には静磁場の時に使う放射ゲージ条件ではなく、別の条件を使います。

電磁波の式を導出するための式は実は別の式も必要で、それは電磁誘導のほうの微分形の式の回転を考えてから、そこにアンペールの法則の微分形を代入するというものです。参考までに初めの形だけ記しておくと次のようになります。
$$\mathrm{rot}\left(\mathrm{rot}\overrightarrow{E}\right)=-\mathrm{rot}\left(\frac{\partial \overrightarrow{B}}{\partial t}\right)=-\frac{\partial }{\partial t}\left(\mathrm{rot}\overrightarrow{B}\right)$$
$$ナブラを使って書くなら、\nabla\times\left(\nabla\times\overrightarrow{E}\right)=-\nabla\times\left(\frac{\partial \overrightarrow{B}}{\partial t}\right)=-\frac{\partial }{\partial t}\left(\nabla\times\overrightarrow{B}\right)$$
アンペールの法則の微分形は最右辺の磁場の回転の部分に代入します。
すると、左辺も右辺も磁場を含まない形の式になるわけです。ここでも、変位電流の項がもし無かったらこの先の計算は上手く行きません。
このような理論のもとで得られる電磁波の定量的な性質と電磁波の実測における性質がよく合っているので、アンペールの法則を変位電流も加えた形で記述した一般形の式も正しいはずであると考えられているわけです。
アンペールの法則による磁場の計算例
アンペールの法則によって磁場を計算できる簡単な例をいくつか挙げます。
(電流が定常電流であるか、変位電流を無視できる状況だけを考えます。)
アンペールの法則を使って磁場を計算する例に多く見られる特徴は、大体が次のようなものです。
- 経路を単純なものに選ぶことで接線線積分を簡単にする事が多い
- 話を単純にする仮定や前提が必要な事が多い(長さを無限とする事や、対称性など)
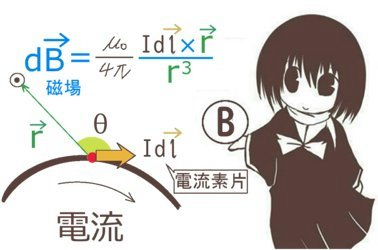
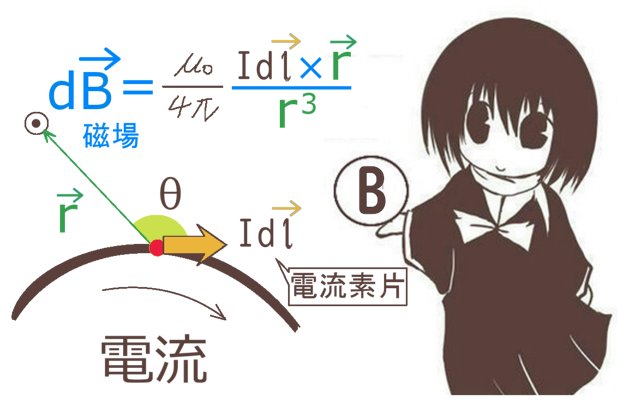
- より詳細を調べるにはビオ・サバールの法則のほうが適している事がある
直線定常電流が作る磁場
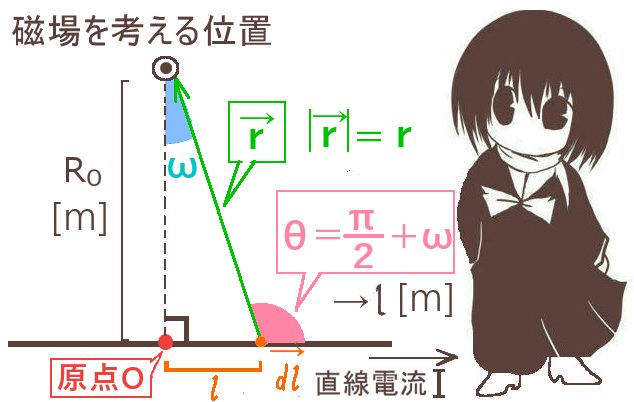
まず、一番簡単な例として直線状の定常電流が作る磁場です。
導線の長さは十分に長い(無限とみなせる)とします。
電流が環状の磁場(導線に対する同心円上で同じ大きさ)を作る事は実験によって知られていたわけですが、その事実も使って計算します。あるいは、磁場の大きさに関しては対称性から同心円上で等しいと仮定します。
磁場が導線を中心とする半径rの円に常に接する方向を向いているとします。
接線線積分において内積はBdlとなり、lを0から2πrまで変化するパラメータとして捉えるか、dl/dθ=r【半径×弧度法の角度=円弧の長さより】と考えると計算ができます。
$$\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\int_0^{2\pi}Brd\theta=[Br\theta]_0^{2\pi}=2\pi Br$$
$$アンペールの法則により\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\mu_0 Iなので2\pi Br=\mu_0 I\Leftrightarrow B=\frac{\mu_0I}{2\pi r}$$
同じ結果はビオ・サバールの法則による計算によっても得る事ができますが、いくつかの条件が分かっていればアンペールの法則を使ったほうが計算が簡単になります。いずれにしても十分に長いとみなせる直線電流が作る磁場の大きさは「導線からの距離に反比例する」という事になります。
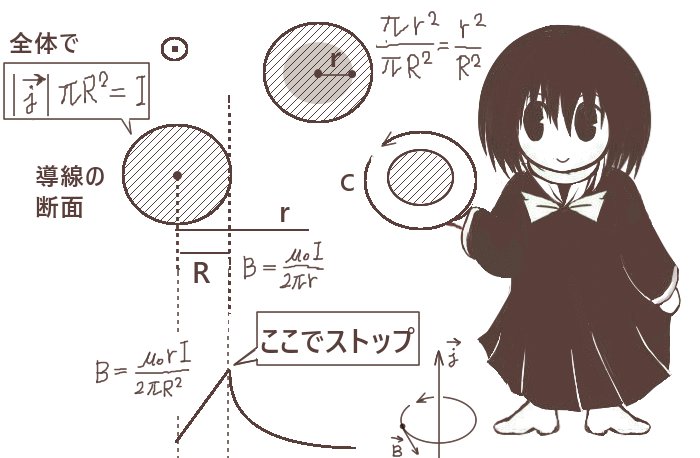
断面積を持つ導線の場合の定常電流による磁場
同じ事は、導線が無視できない断面積Sを持っていても形状が円柱状で、定常電流である限りは導線の外側においては中心からの半径で測ると同じ結果になります。
他方で、その場合は「導体内部」の磁場を考える事もできます。
今、導体断面における電流密度ベクトルが一様であるとします。
アンペールの法則においては閉曲線の内部を通過する電流だけを考えればよい事になります。
導線の半径をR、考えている半径をr<Rとすると半径rの円内の電流は全体のr2/R2倍なので導線の断面積全体の電流をIとすれば
2πBr=μ0I(r2/R2) ⇔ B=μ0rI/(2πR2)
つまり、rを増やしていくと導体内では磁場は大きくなっていく計算です。
また、r=Rになった時点でB=μ0I/(2πr)という導線外部の時の式と同じになり、
そこからは磁場の大きさは距離ごとに減っていく事になります。
この結果は導線外部の磁場の大きさB=μ0I/(2πr)を考えた時に、
rを減らしていっても実際の所は磁場はそこまで大きくならない事も示しています。反比例の関係という事はrが0に近ければ値はやたらと大きくなり得るわけですが、実際は導線の表面にぶつかる時点からはrを減らすと磁場も小さくなっていくと考えられるわけです。
導線の内側(導線の半径:R r≦Rの範囲) $$B=\frac{\mu_0rI}{2\pi R^2}$$ 導体の外側(断面積が無視できる導線の場合と同じ。 r≧Rの範囲) $$B=\frac{\mu_0I}{2\pi r}$$
トロイダルコイル(環状ソレノイド)
トロイダルコイルとは、食べ物のドーナツのような立体的な形(トーラス)をしたコイルです。
「環状ソレノイド」と呼ぶこともあります。一見複雑そうにも思えますが、アンペールの法則を適用すると意外に考察がしやすい例の1つとなっています。
てきとうな半径の円が断面であるトーラスに導線が一様かつ密に巻かれており、
巻数の合計がNで、トーラス全体の中心から断面の中心までの距離がRである隙間が無いトロイダルコイルになっているとします。
巻線に定常電流Iが生じている時、断面の中心における磁場の大きさは次のようになります。
$$B=\frac{\mu_0NI}{2\pi R}$$
また、断面中心を原点とした極座標(r,θ)で、トーラスの外側に向けて基線(角度を0に考える線)を考えると、
断面内における断面中心以外の場所での磁場の大きさは次のように表せます。
$$B=\frac{\mu_0NI}{2\pi (R +r\cos\theta)}$$
また、理想的なトロイダルコイルでは外部の磁場は0である事を示せます。
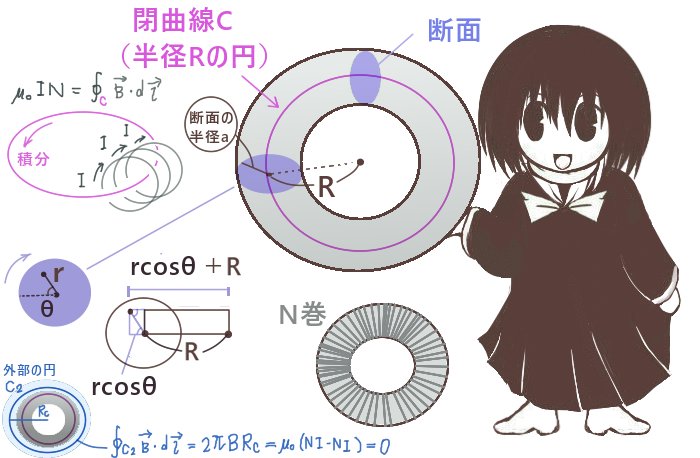
トロイダルコイルの断面の中心を結んだ円を考えて、これをアンペールの法則で周回の接線線積分を考える閉曲線Cとします。
すると、閉曲線C内を通過する電流は巻数の合計Nと1本の導線ごとの電流の大きさの積という簡単な式で表せます。つまり電流の合計をISとすると、 IS=NIです。
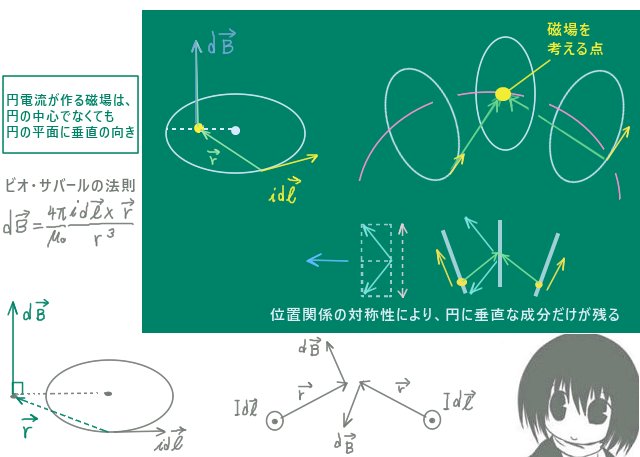
形状の対称性と、円状の電流は面に垂直な磁場を作る事(これはビオ・サバールの法則で導出するのが普通です)により、磁場の向きは考えている円(閉曲線C)に接する方向であり大きさはその円周上でどの位置でも同じと考えられます。
コイルの1巻き分以外の部分からの影響にも注意する必要がありますが、両隣の電流の向きに注意すると断面に平行な成分はプラスマイナスで打ち消し合って、断面に垂直な成分だけが残る事になります。つまり、閉曲線として考えている円に磁場の向きが接する事は保たれるわけです。
そこで、直線定常電流が作る磁場と同じく、lが0から2πdまでの通常の積分として磁場の大きさが計算ができます。(変数変換して角度で考えても同じです。)
$$\oint_C\overrightarrow{B}\cdot d\overrightarrow{l}=\int_0^{2\pi R}Bdl=2\pi BR$$
$$定常電流の時のアンペールの法則により2\pi BR=\mu_0NI\Leftrightarrow B=\frac{\mu_0NI}{2\pi R}$$
断面内の任意の位置の場合は、角度のとり方に注意すると閉曲線として半径R+rcosθの円を考えればよい事になります。(断面の中心よりも少し外側であればθが-90°から+90°の範囲、断面の中心よりも少し内側であればθが90°から270°の範囲で、Rに対してrcosθの分だけ少し大きいか小さいかの値になります。)
この場合に磁場ベクトルが常に円に接するかどうかには気を付ける必要がありますが、ビオ・サバールの法則を考えると円電流が作る磁場は円の中心の位置では無くても円の面に垂直になる事が分かります。(磁場を考える点が円と同じ平面にあれば、円の接線ベクトルと円周上から磁場を考える点までのベクトルとの外積ベクトルは円の平面に対して垂直。)
そこでトロイダルコイル全体が持つ対称性も合わせて考えると、接線線積分も断面中心を通る円で考えた時と同様に行う事ができます。
$$2\pi B(R+r\cos \theta)=\mu_0NI\Leftrightarrow B=\frac{\mu_0NI}{2\pi R}(R+r\cos \theta)$$
トロイダルコイルの外部についても接線線積分は同じように考える事ができます。電流に関しては全巻き数について逆向きの電流が加わるので、円として考える閉曲線の半径をRcとすると
2πBRc=μ0(NI-NI)=0より、B=0
この結果は、トーラスの内側の空間に対して適用しても同じ事が言えます。