カテゴリー: 三角関数

無限積とバーゼル問題 ― 解答とその厳密性

恭平

無限積とは積の因数の数が有限ではなく無限であるものを指します。無限級数が無限個の項の和を考えるものであるのに対して、無限積は無限個の因数の積を考えるわけです。無限積も無限級数と同様に収束する場合と発散する場合があります。

無限積の理論は、実は対数を使う事によって無限級数の理論を当てはめる事ができます。これはやや純数学的な側に偏った理論と言えそうですが、無限積はオイラーのバーゼル問題（π２／６＝１＋１／４＋１／９＋１／１６＋・・・【Basel Problem】の証明）の解決において無限級数を「無限積に因数分解する」という形で、数式的には興味深い数学の問題と深く関わっています。【πは円周率です。】

尚、収束する無限級数に対して因数定理（多項式に数αを代入して０になる時にその多項式はｘーαを因数に持つ）を無限積の形で適用できる事を厳密な形で確認するには、個別の関数ごとに解析学的に複素関数論まで含めて詳しく見る必要があり、簡単に一般化できない難しさがあります。

「バーゼル問題」自体は、次の式はどのような値に収束するか？（あるいは発散するのか？）という問題です。 $$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{3^2}+\frac{1}{4^2}+\dots\left(=\sum_{n=1}^\infty\frac{1}{n^2}\right)$$ この式が「円周率の２乗を６で割った値」に収束するという解答を初めて得たのがオイラー氏とされます。 $$1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{3^2}+\frac{1}{4^2}+\dots=\frac{\pi^2}{6} が解答$$

無限積の例：オイラーの「バーゼル問題」の解答と証明

数列｛Aｎ｝がある時、各項それぞれの全ての積Ａ１Ａ２Ａ３・・・Ａｎー１Ａｎに対してｎ→∞を考えたものが無限積の式になります。

さて、これが一体何に使えるか？という事に関して数学者（理論物理学者等でもある）のオイラー氏は三角関数の sin x が x＝ 0，±π，±2π，±3π，・・・で０になる事から【特定の場合において】因数定理が利用できる「はず」だと考えたと言われています。すなわち無限積に因数分解するという事です。そんな事ができるのでしょうか？kを定数とします。

$$ とある無限積： k(x-0)\left(x-\pi\right) \left(x+\pi\right) \left(x-2\pi\right) \left(x+2\pi\right) \left(x-3\pi\right) \left(x+3\pi\right)\dots $$

$$= kx\left(x^2-\pi^2\right) \left(x^2-2^2\pi^2\right) \left(x^2-3^2\pi^2\right)\dots $$

とりあえず、このような無限積自体を考える事は可能です。これが三角関数 sin x の「展開」になり得るのかはひとまず置いておきましょう。

ところで、同じ考え方をすると同じ形の無限積は sin x を含む別の関数でも可能な「はず」です。そこでオイラー氏が目を付けたのが (sin x)／x だと言われています。この関数は ｘ→０ で１に収束します。また、sinx をテイラー展開すると (sin x)／x は次式になります。

$$\frac{\mathrm{sin}x}{x}=1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots$$

さて、この式を無限積に因数分解「できるとしたら」、ｘ＝０で値は１に収束する必要があります。さらに x＝ ±π，±2π，±3π，・・・でも値が０になる必要があります。

そのような因数は（１ーｘ／π），（１＋ｘ／π），{１＋ｘ／(２π)}，{１－ｘ／(２π)} ，・・・の形しかあり得ないとオイラー氏は考えたとされます。【※ｘ＝０では値が０にならないと分かっているので単独のｘは因数には含まれません。】

$$因数が\left(1- \frac{x}{\pi}\right)\left(1+ \frac{x}{\pi}\right)\left(1- \frac{x}{2\pi}\right)\left(1+ \frac{x}{2\pi}\right)\left(1- \frac{x}{3\pi}\right)\left(1+ \frac{x}{3\pi}\right)\dots だとすると、$$

$$1-\frac{x^2}{3!}+\frac{x^4}{5!}-\frac{x^6}{7!}+\dots$$

$$=\left(1- \frac{x}{\pi}\right)\left(1+ \frac{x}{\pi}\right)\left(1- \frac{x}{2\pi}\right)\left(1+ \frac{x}{2\pi}\right)\left(1- \frac{x}{3\pi}\right)\left(1+ \frac{x}{3\pi}\right)\dots$$

$$=\left(1- \frac{x^2}{\pi^2}\right)\left(1- \frac{x^2}{2^2\pi^2}\right)\left(1- \frac{x^2}{3^2\pi^2}\right)\dots$$

ここで、ｘ２の項だけに着目します。この式がｘ＝０以外の任意の実数で成立するとするとｘ２の係数は一致しなければなりません。すると、次式が成立するはずです。

$$-\frac{1}{3!}=- \frac{1}{\pi^2}- \frac{1}{2^2\pi^2} -\frac{1}{3^2\pi^2}-\dots$$

$$すなわち、\frac{\pi^2}{6}=1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\dots$$

これが無限積を使ったバーゼル問題の解答 π２／６＝１＋１／４＋１／９＋１／１６＋・・・（および導出過程・証明）になります。

対数による無限積の無限級数への変換

さて、有限のｎの値で止めてある積Ａ１Ａ２Ａ３・・・Ａｎー１Ａｎに対して対数を考えると、積は和の形に変形されます。対数の底は本質的には何でも良いのですが、微積分との相性から自然対数を考えるとします。（対数の底はe＝２.７１８・・・であり、その時の log e を ln【ログ ナチュラル】で略記する慣例をここでは使います。）

ln（Ａ１Ａ２Ａ３・・・Ａｎー１Ａｎ）＝ lnＡ１＋lnＡ２＋lnＡ３＋・・・＋lnＡｎー１＋lnＡｎ　ですから、ｎ→∞の時に右辺の無限級数が収束する【極限値との差をいくらでも小さくできる】のであれば左辺も収束し、対数の真数であるＡ１Ａ２Ａ３・・・Ａｎー１Ａｎについてｎ→∞とした時の無限積も収束する事になります。

そのため、無限級数lnＡ１＋lnＡ２＋lnＡ３＋・・・の収束性が分かれば無限積の収束性も分かるという理論となっているわけです。

無限積の収束性に対する基本的な考え方

$$\prod_{n=1}^{\infty}a_n =a_1 a_2 a_3 a_4 \dotsに対して、$$ $$\mathrm{ln}\left(\prod_{n=0}^{\infty}a_n\right) =\sum_{n=1}^{\infty}\left(\mathrm{ln}a_n\right)= \mathrm{ln}a_1 +\mathrm{ln}a_2 +\mathrm{ln}a_3 +\mathrm{ln}a_4 +\dots を考える。$$

ちょっとした注意点として、「そもそもの無限積が０である時には無限積は発散するという事にする」という定義上の決まりがあります。これは、０に等しい無限積の対数をとると無限大に発散してしまう事が関係しています。

関連する事として、無限積にマイナスの数が無限個含まれる場合には収束しませんので無限積に含まれるマイナスの数は最初から有限個として考えるのが普通です。あるいは、符号が全てプラスとしてもし収束するなら後から有限個のマイナスの符号を乗じても収束しますので最初から無限積の因数は全てプラスであるとして考えます。

さて、対数で考えるとかえって難しくなるのでは？とも思えますが、実は次の便利な関係式があります。

$$有用な式：x>0 において、0<\mathrm{ln}(1+x)<x$$

【ｘ＝ln eｘで、１＋ｘとeｘの大小を比較します。微分をすると導関数はそれぞれ１とeｘで、ｘ＝０でともに１です。（グラフはｘ＝０で接する事になります。）他方、任意のｘ＞０では１＋ｘの導関数は定数１で一定であるのに対し、eｘの導関数は単調増加です。そのため、ｘ＞０の範囲においては
１＋ｘ＜eｘであり、 ln(1+x) ＜ｘです。】

$$もう１つの式：a_n >0 の時には1+\sum_{n=1}^{\infty}a_n<\prod_{n=1}^{\infty}(1+a_n)$$

【右辺を展開すると、左辺＋プラスの数の形になるので成立します。】

これらの式を使うと、次の定理を証明できます。

無限積に関する定理の１つ

$$任意の自然数ｎに対しa_n >0 のもとで、$$ $$\prod_{n=0}^{\infty}(1+a_n)が収束する\Leftrightarrow \sum_{n=1}^{\infty}a_nが収束する$$

つまりこの形の場合には、最初は対数を考えるけれども収束性は対数がない無限級数の形を調べればよいという事になります。

$$証明：0<1+\sum_{n=1}^{\infty}\mathrm{ln}(1+a_n)<1+\sum_{n=1}^{\infty}a_n<\prod_{n=1}^{\infty}(1+a_n)$$ $$まず、-1<\sum_{n=1}^{\infty}a_n<-1 +\prod_{n=1}^{\infty}(1+a_n)$$ これによって無限積が収束⇒無限級数側は有界な単調増加数列となり収束。 $$次に、-1<\sum_{n=1}^{\infty}\mathrm{ln}(1+a_n)<\sum_{n=1}^{\infty}a_n$$ 無限級数側が収束⇒無限積の対数も有界な単調増加の数列なので収束し、もとの無限積も収束する事になります。

さて、バーゼル問題を無限積によって解く方法はこれに当てはまりそうで、微妙に当てはまりません。負の項が含まれるからです。しかし条件を追加すると別の定理が成立します。

バーゼル問題と無限積の収束性

無限積に関する２つめの定理を適用すると、バーゼル問題での無限積は少なくとも「収束する」事は言えます。しかし、実は無限積の収束性はより一般的には単純ではなく複雑です。特定の形をしている場合にのみ、比較的容易に収束性の判定ができます。無限を含む場合に因数定理がいつでも成立するのか？という問題も単純ではありません。バーゼル問題の解答は「天才的・画期的」な発想であるとともに、無限を含む場合の解析学的な複雑さと難しさも含んでいるものと言えるのです。

無限積に関する定理がもう一つ存在します。条件追加をする事で、もう少し広い範囲の関数の収束性が分かるというものです。

無限積に関する定理その２

$$ある自然数nに対しa_n ＜０となる項を含んでいても、$$ $$\sum_{n=1}^{\infty}{a_n}^2が収束する時には、\prod_{n=0}^{\infty}(1+a_n)が収束する\Leftrightarrow \sum_{n=1}^{\infty}a_nが収束する$$

この定理の証明は、|ｘ|＜１／２の時に次の式が成立する事を示す事によって行われます。

$$不等式：|\mathrm{ln}(1+x)-x|\le x^2$$

左辺で絶対値を考えるのは、無限級数が「絶対収束」する事を示すためです。（絶対収束する無限級数は収束するため。）少し面倒ですが、不等式の関数を微分して導関数を調べると証明できます。

バーゼル問題に話を戻しますと、任意のｘ≠０において無限積の因数を２組ごとに乗じて１つの因数にした形を見てみると、無限積ではなく無限級数を考えた場合には次式を見れば良い事になります。

$$-\frac{x^2}{\pi^2}\left(1+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\dots\right)$$

このうちの後者の無限級数の因数は、バーゼル問題とは別の方法で値は「収束する」事が実は分かります。【公比が１／２の等比級数（幾何級数）の極限値より小さい事が示せて、有界な単調増加数列となるため。】ですので(sinx)／x を「因数分解」した無限積は少なくとも収束するという妥当性は持っているわけです。他方で sinx を同じ方法で無限積にできるかというと、話がややこしくなります。(sin x)／x を無限積に展開できるならば両辺にｘを乗じればそれが解答という事になりそうですが、どのような時にでも無限積が収束するかといえばそうではないので注意が必要になるのです。バーゼル問題の解答の導出は「鮮やか」であるだけに、無限に関する厄介で面倒な問題が含まれているのは残念な事実ではあります。

注意すべき大事な事は、バーゼル問題の解答は「素晴らしく正解」ですが、同じような無限積の適用を一般化できるかというと遺憾な事ながら必ずしもそうではない、という事かと思われます。

正弦関数の無限積展開と複素関数論

さて、バーゼル問題の解答の「証明」や正弦関数の無限積の「因数分解」についてもっと式で厳密に表せないかというと、実は方法があります。ただしその導出の途中で複素関数論の少し面倒な理論を挟むので、その点に注意が必要です。

まず正弦関数の「因数分解」ですが、結論を言うと厳密にできます。結論は次式です。

正弦関数 sin z の無限積展開

z は実数だけでなく複素数でも成立します。 $$\sin(\pi z)=\pi z\prod_{n=1}^{\infty}\left(1-\frac{z^2}{n^2}\right)$$ この式でπｚ＝ｘと置き直すと、ｚ＝ｘ／πに注意して、次式が成立します。 $$\sin x=x\prod_{n=1}^{\infty}\left(1-\frac{x^2}{\pi^2n^2}\right)$$ すなわち、(sin x)／x が「因数分解できるはず」 と考えた式からの導出結果に一致します。

証明を簡易的にですが述べます。

結論の無限積の「対数微分」が直接的に重要な部分となります。対数微分の公式（本質的には合成関数の微分）{ln f(x)}’＝f ‘(x)／f(x) を使用します。

まず無限積の対数を考えて無限級数の項別微分をする（項別微分可能です）と次式です。

$$\frac{d}{dx}\mathrm{ln}\left\{x\prod_{n=1}^{\infty}\left(1-\frac{x^2}{\pi^2n^2}\right)\right\}= \frac{1}{x}+\sum_{n=1}^{\infty}\left(\frac{-2x}{\pi^2n^2}\cdot \frac{\pi^2n^2}{\pi^2n^2 -x^2}\right)$$

$$=\frac{1}{x}+\sum_{n=1}^{\infty}\frac{2x}{x^2-\pi^2n^2 }$$

無限積の各項を１つの分数にまとめてから対数微分の公式を使っています。（積の微分公式の使用ではなく、対数で和の形にしてから各項で対数微分している事に注意。）

この式の結果が、実は余接関数 cot x ＝(cos x)／(sinx) の無限級数展開に定数を乗じたものに等しいのです。

公式：余接関数の無限級数展開

０以外の複素数ｚ（実数含む）に対して次式が成立します。 $$\pi\mathrm{cot}(\pi z) =\frac{1}{z}+\sum_{n=1}^{\infty}\frac{2z}{z^2-n^2}$$ この式で再びπｚ＝ｘと置き直すと、ｚ＝ｘ／πに注意して、次式が成立します。 $$\pi\mathrm{cot}x =\frac{\pi}{x}+\sum_{n=1}^{\infty}\frac{2\pi x}{x^2-\pi^2n^2}$$ $$両辺を\piで除すると、\mathrm{cot}x =\frac{1}{x}+\sum_{n=1}^{\infty}\frac{2x}{x^2-\pi^2n^2}$$

【証明は？：この式の証明には複素関数論を使うのが一般的ですので、別の記事にて改めて紹介したいと思います。】

ところで、余接関数の分母は余弦関数で、これは正弦関数の導関数です。

つまり、cot x ＝(cos x)／(sinx) ＝(sin x)’／(sinx)＝(ln sinx)’ とも書けます。

無限積の対数微分と正弦関数の対数微分が一致するので元の無限積は定数k を使って k sin x となり、(sinx)／x のｘ→０での極限値が１である事からｋ＝１で無限積は sin x に等しい事になります。

正弦関数の無限積展開が証明されれば、(sinx)／x の無限積展開も正当化され、バーゼル問題の解答の導出も厳密に「正しい」という事になります。

オマケとして、余弦関数 cos x も無限積展開する事ができます。次式です。 $$\cos x =\prod_{n=1}^{\infty}\left\{1-\frac{4x^2}{\pi^2(2n-1)^2}\right\}$$ これも基本的に複素関数論の観点から導出されます。

光の二重スリット干渉実験【ヤングの実験】

恭平

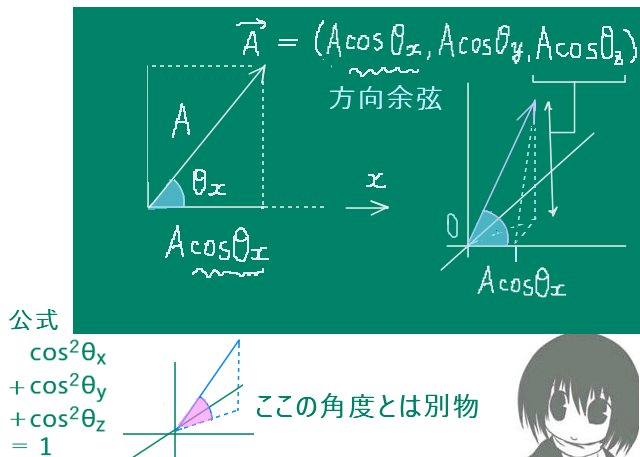
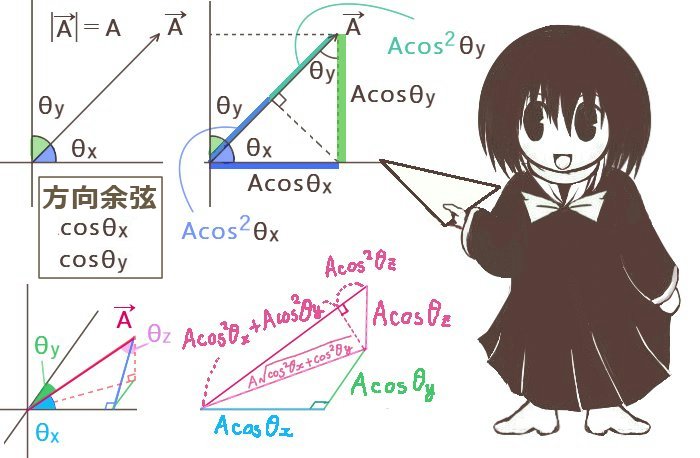
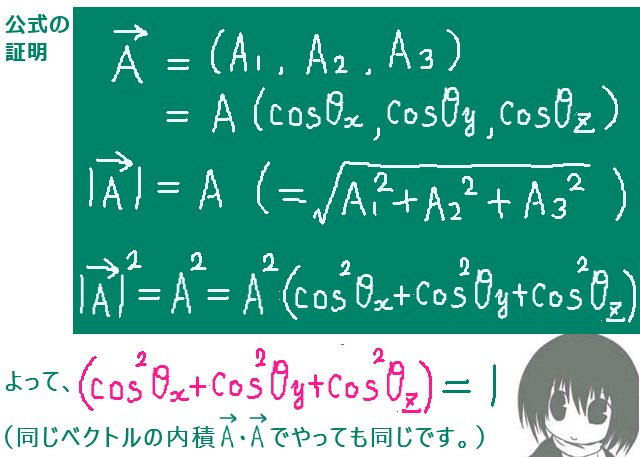ヤングによる実験をもとにしている二重スリットを使った光の干渉実験は光の波動性を確認できるとともに、可視光の波長の概算的な測定ができる実験です。
また、光の干渉を利用した種々の干渉計のもとになっているという意味での重要性も持ちます。
数式的には三角比も含めた平面幾何的な考察によって、光の異なる２つの経路の長さの差（光路差）を計算する事により波長を含んだ関係式を導出できます。

この実験では光のコヒーレンス（可干渉性）の考え方も、重要な要素の１つとなっています。

模式図としては、分かりやすさのためにスリットの並びとスクリーン上の干渉縞が画面や紙面に対して縦方向に現れるように書かれる事が多くこの記事でもそうしていますが、実際の実験ではその方向が地面に対して平行であるようにする事がどちらかというと多いと思われます。

この記事では古典論での光の波動性を示す干渉実験について説明しています。
量子力学的な意味での二重スリット干渉実験もありますが、そちらでは粒子（とみなせる塊）を１つずつ、ある程度の時間の間隔をあけて二重スリットに向けて打ち出すという手法がとられます。ただしスリットのどちらかを狙い打ちするように打ち出すのではなく、スリットを通過する際に「どちらのスリットを通過したか不確定である」ようにします。そこがヤングによる干渉実験と異なる部分となります。量子力学的な二重スリット干渉実験は２０世紀後半以降、電子や光子、一部の分子（比較的分子量が大きいものも含む）などについて行われています。

人の目に見える領域の光である「可視光線」の波長は実は非常に短く、
「ナノメートル」や「マイクロメートル」の単位のスケールでの長さとなります。
単位についてのメートルとの関係は次の通りです。
【ｎｍ】・・・「ナノメートル」　１【ｎｍ】＝１０－９【ｍ】
【μｍ】・・・「マイクロメートル」　１【μｍ】＝１０－６【ｍ】
【ｍｍ】・・・「ミリメートル」　１【μｍ】＝１０－３【ｍ】
「センチメートル」【ｃｍ】は１０－２【ｍ】（百分の１メートル）になります。

■関連サイト内記事：

スリットとは【実験の概要】

スリット（slit）は物理の実験用に使われる板などに開けた非常に細い隙間の穴の事であり、
二重スリットあるいはダブルスリット（double slit, double-slit ）は非常に近い間隔でスリットが２つある構造を指します。

slit とは英語において通常の語としても使われており、
「（刃物等による）切れ目」とか「切れ目を入れる」という意味で使われます。
「スリット」という言葉は実は現代日本語でも使われる時があり、パンや服、その他の色々なものに施された切れ目や溝、細い穴を指してスリットと言う事があります。

光の干渉（「かんしょう」）を調べる実験では、二重スリットにおけるそれぞれのスリットから光を出してスクリーン上に当てて波が強め合う位置（明るくなる）と弱め合う位置（光がなく暗く見える）が現れる事を見ます。それが縞模様のように見える事が多いので明暗のパターンの模様を干渉縞（「かんしょうじま」）と呼ぶ事もあります。
また、ある位置で２つ以上の光の重ね合わせの事を干渉光と呼ぶ事があります。

干渉は波動一般に対して起こる現象です。
ある位置で２つ以上の波の波形がぴったりと重なっていると合計として１つの大きな振幅の波となって強め合い、逆に波の最大値（プラスの値）と最小値（マイナスの値）が重なってしまうと波がつぶれて振幅が任意の時刻で０になってしまい弱め合います。
ここでは２つの光線の干渉を考えますが、３つ以上の光線の干渉を考える事もできます。

光には結論から言うと波動性がありますが、もし波動性が無くて「粒子（の集まり）としてだけ」振る舞うとしたらそのような縞模様ができる必然性がないので、干渉縞が現れる事が波動性を持つ事の根拠であるとして物理学的には解釈されているわけです。

実験用に使う二重スリットには色々なものがあり得ますが例としては、
１つのスリット自体の幅は０.１【ｍｍ】程度（光が回折するのに必要なおおよその細さ）、
２つのスリット間の距離は０.１～１.０【ｍｍ】程度のものがあります。
（スリットが開けられているスリット板の大きさは、例えば横１０ｃｍ，縦５ｃｍ程度など。）

水面の波が平面波として進行しているような場合は位相が揃っている波が隙間に入ります。
基本的に、光の干渉を調べる時にも同じ状況を作る必要があります。
スリットから出た波が広い範囲に広がっていくようにするには波の回折の現象を利用します。
可視光線の干渉の場合、波が強め合う位置は明るい点や線となって見えて、波が弱め合う位置は明るさが無く暗く見えます。

１つ１つのスリットからは１方向だけに光線が出るのではなく、非常に広い範囲にたくさんの光線が広がって行く形になります。これは波の回折現象を利用しており、波動性がなければ干渉同様に発生しない現象でもあります。

そのためにスクリーン上の各点では２つのスリットから出た光線のあらゆる重ね合わせが連続的に映し出される事になり、その中で特に光が同位相で強め合う部分と、半波長だけずれて弱め合う部分が目立って見えて干渉縞が形成されるわけです。

光は非常に細いスリットを通過する事ができます。
ただし、二重スリットの実験においてはスリットは意図的に細いものを使います。それはスリットにおいて波の回折を起こさせるためです。
回折とは波が小さい隙間に入り込み、そこから出る時に同心円か同心球状に大きく広がっていく現象です。イメージとしては水面に何か物が落ちた時に波紋が広がっていくような事が波が隙間から出る時に起きる事を指します。しかし回折はどんな波に対してどのような隙間に対しても起こるわけではなくて、基本的には波の波長が短いほど短い隙間が必要になります。
そして結論から言うと可視光線（色として人に見える領域の光）の波長はおおよそ
４００【ｎｍ】～７００【ｎｍ】の範囲であり、標準的な音波と比較しても非常に短い波長です。
光の干渉に使うスリットに「細さ」が求められるのはそのためであり、基本的に可視光線のて回折を起こさせるためには０．１ミリメートル程度かそれ以下の細さのスリットを使う必要があると言われます。

模式図としては、分かりやすさのためにスリットの並びとスクリーン上の干渉縞が画面や紙面に対して縦方向に現れるように書かれる事が多くこの記事でもそうしていますが、実際の実験ではその方向が地面に対して平行であるようにする事も多いです。
光源としては広がりが十分狭い「点光源」とみなせるものを使う必要があります。
単色光に近い光の干渉縞の明線の間隔はほぼ一定値です。
ただし、スクリーンの原点部分から離れるにつれて光の強度は小さくなっていくので明線の明るさも少しずつ減っていきます。

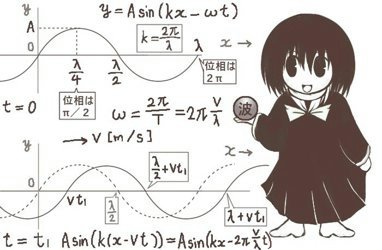
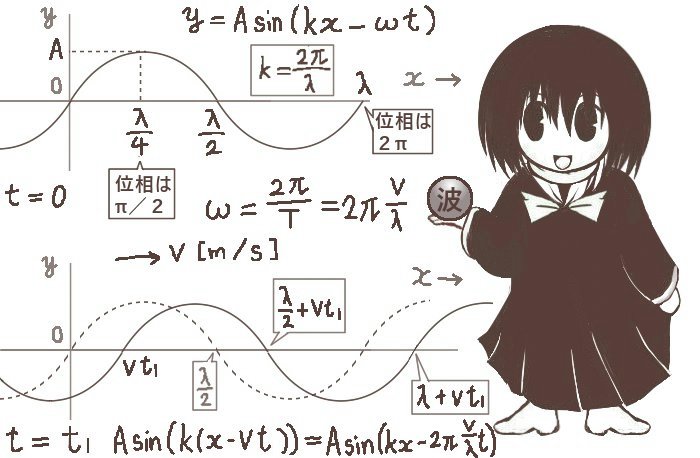
波動が正弦波であるとすると、干渉の効果を式で表す事もできます。
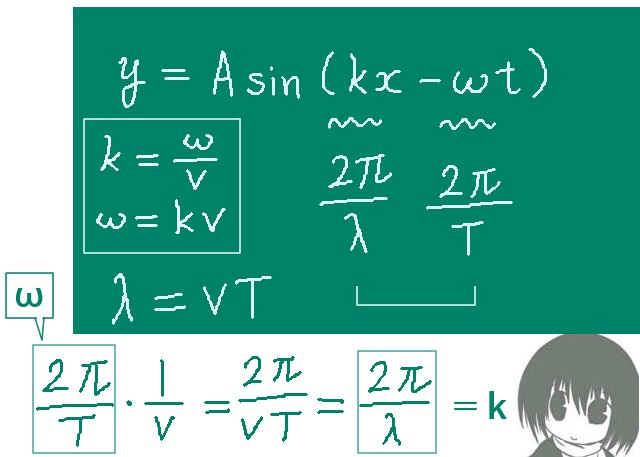
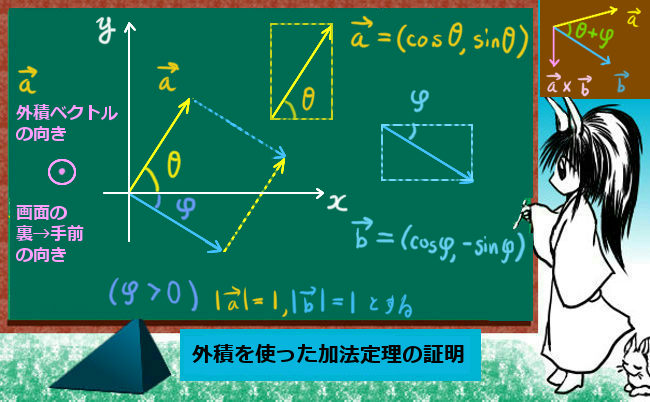
２つの光路の大きさをそれぞれＲ１とＲ２とすると２つの波はそれぞれ ｙ＝Ａsin(ｋＲ１－ωｔ)，ｙ＝Ａsin(ｋＲ２－ωｔ)で表され、それらの波の重ね合わせは三角関数の和積の公式または加法定理により次式で計算できます$$A\sin(kR_1-\omega t)+A\sin(kR_2-\omega t)$$ $$=2A\sin\left\{\frac{k(R_1+R_2)}{2}-\omega t\right\}\cos\frac{k(R_1-R_2)}{2}$$この式で余弦の部分は時間に依存しないのでＲ１とＲ２の値によって決まる「振幅」の一部だと見なせます。余弦の部分は時間に依存せず、光路差（の絶対値）| Ｒ１－Ｒ２|にのみ依存して干渉光が強め合ったり弱め合ったりする事を表します。

公式を使った後の余弦の部分は（A－B）／２の代わりに（B－A）／２を考えても余弦の値は同じになります。

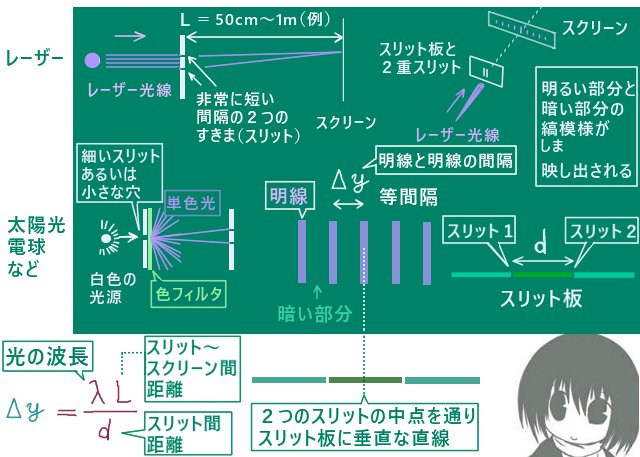
光の波長と干渉縞に対して成立する関係式

スリット板の中央から垂直に線を引いて、
その線とスクリーンとの交点をここでは「スクリーン上の原点」と呼んでおきます。
スクリーンとスリット板は平行になるようにきちんと立てます。（片方だけ傾いていると結果がおかしくなります。）

光の干渉に関する二重スリットの実験の結果に使う数値は次の通りです。波長を除くと、使用する記号は他のものが使われる事もあります。

  • λ【ｍ】光の波長（可視光ではおおよそ４００【ｎｍ】～７００【ｎｍ】の範囲）
  • L【ｍ】スリット板中央からスクリーン原点までの距離（数十【ｃｍ】～３【ｍ】の範囲等）
  • ｄ【ｍ】スリット板における２つのスリット間の距離（０.１～１.０【ｍｍ】程度）
  • ｙ【ｍ】スクリーン上における、原点部分からの距離。（スリット板に平行な方向。）
    （座標のようにプラスマイナスの値で考える事もあります。）
  • Δｙ【ｍ】スクリーン上に現れる明線間の距離（数ミリメートル～数センチメートル程度）

その他に、整数ｎや奇数２ｎ＋１などを式中で使います。具体的な数値は色々な場合があり得ますが、光の波長の範囲を考えると特定の数値を極端に大きくしたり小さくし過ぎたりすると上手く測定ができない事につながります。
以下に示す関係式を使う時にはスリットとスクリーン間の距離Ｌは、ｙやｄと比べて十分大きい値になっている必要がありますが、それについても、極端にLが大きすぎてもおかしくなります。

スリット間の距離については「ｄ」の文字が使われる事が多いのでここでもそうしていますが、微分や微小量とは直接的に関係はありません。ただしそれなりに短い間隔ではあります。

光源としてはレーザー光線のように単色とみなせて位相が揃っている（コヒーレントである）ものを使うのが望ましく、
白色光を使う場合は小さい穴に通して点光源化し、色フィルタ等を置いて多くの波長の光を除外して単色に近くなるようにします。そこから回折により同じ位相の揃った単色に近い波が広がって進行し、二重スリットに至るようにします。

二重スリット実験での測定で光の波長を表す式

二重スリットによる光の干渉実験において、
上記の量と光の波長の関係式は次のように表されます。
■波長をL，ｄ，Δｙで表す式 $$\lambda = \frac{(\Delta y)d}{L}【波長を表す式】$$ $$\Leftrightarrow \Delta y=\frac{\lambda L}{d}【明線の間隔を表す式】$$ ■光路差が波長の整数倍になる事および明線の位置を表す式
（ｎは整数。ｎ＝０の時はスクリーン中央、ｎ＝１の時はΔｙを使った式と同じです。） $$n\lambda=\frac{yd}{L}$$ $$\Leftrightarrow y=\frac{n\lambda L}{d}$$ ■ｙ／Ｌ＝tanθ を使った場合の表記
（θが小さい値の時に成立。）
$$n\lambda=d\tan\theta≒d\sin\theta≒d\theta$$

波が弱め合う条件を考える場合にはｍを「奇数」としてｍλ／２を考えて
ｙｄ／Ｌ≒ｍλ／２とするか、
あるいは「波長の整数倍に半波長が加わっている」と考えて
ｙｄ／Ｌ≒(ｎ＋１／２）λのようにします。
奇数ｍをｍ＝２ｎ＋１と書けば
ｍλ／２＝(ｎ＋１／２）λとなるので、上記２式は同じものです。

可視光の波長のおおよその範囲が
４００【ｎｍ】～７００【ｎｍ】＝４×１０－７【ｍ】～４×１０－７【ｍ】なので、
上記の関係式Δｙ＝λＬ／ｄから判断すると
Lやｄの値によってはΔｙの値が小さくなり過ぎて
「干渉縞がつぶれてしまって測定できない」という事もあり得る事が分かります。

仮にｄ＝０.１０【ｍｍ】＝１.０×１０－４【ｍ】でＬ＝１.０【ｍ】であるとします。
この時にλ＝５００【ｎｍ】＝５.０×１０－７【ｍ】の光を光源に使うとすると
Δｙ＝λＬ／ｄ＝５.０×１０－3【ｍ】＝５.０【ｍｍ】となり、
おそらく目視で干渉縞を確認できるだろうという計算になります。
（ｎ＝１～４くらいまではL がｙに対して十分大きいという前提条件も確認できます。）

可視光の波長はいわゆる「色」（普通の赤、青、紫などの色）で特徴づけられます。白色に関しては色々な波長の光が混ざったものです。
（黄寄りの赤・紫寄りの青・緑の光を混ぜると大体白色になるとされます。）
また「物体の色」に関しては白色光等から特定の波長の光が吸収されて、
残りが反射される事で「補色」が見えているというのが一般的に言われる事です。

波おおよその波長
特に光では幅がある		備考
紫色の光約４００
～４５０【ｎｍ】付近		約380【ｎｍ】を下回ると紫外光
（基本的に人の目では見えない）
青色～
水色の光		約４５０
～５００【ｎｍ】付近		紫色・緑色との境界は曖昧
緑色の光約５００
～５５０【ｎｍ】付近		水色・黄色との境界は曖昧
黄色～
橙色の光		約５５０
～６００【ｎｍ】付近		緑色・赤色との境界は曖昧
赤色の光約６００
～７００【ｎｍ】付近		約780【ｎｍ】を超えると赤外光
（基本的に人の目では見えない）
音波約１.７１５【ｍ】空気中，２０【℃】２００【Hz】で
音速約３４３【ｍ／ｓ】の場合
空気中の音波に比べると可視光の波長は非常に短いという観測結果が得られています。
ただし光でも目に見えない領域では種類によっては波長が長く、
例えばラジオ波と呼ばれる領域だと波長が１【ｍ】を超える事もあります。
逆に紫外線やＸ線の領域だと波長は可視光よりもさらに短くなります。

可視光のそれぞれの「色」にも幅があるわけで、例えば「紫色」は大体４００【ｎｍ】付近の色と言う事はできても「ぴたりと３９７ナノメートルの色」のようにはなかなか言えません。しかし物理的には同じ紫色でも具体的な測定対象の光に対して「どのような紫色なのか」を波長によって定量的に表す事ができて（それに意味があるのか、活用の仕方は何かという事はまた別の議論として）、その測定方法の１つとして二重スリットによる干渉実験があるわけです。

関係式の導出（図形的考察）

スクリーン上の原点からｙ【ｍ】の位置に向かう２つのスリットからの光線に着目して、
「１つの光線に対するスリットからスクリーン上の点までの距離（光路の長さ）」の差
である光路差を図から計算する事を考えます。
この計算はいくつかやり方があって、ここではそのうちの２つを説明します。

図の見た目は一見単純なのですが意外と結構くせもので、
「スリット板～スクリーン間の距離Lがｙやスリット間距離ｄに対して十分大きい」という条件から近似（角度や平行関係含む）を行わないと関係式の導出がうまくできないので注意が必要です。

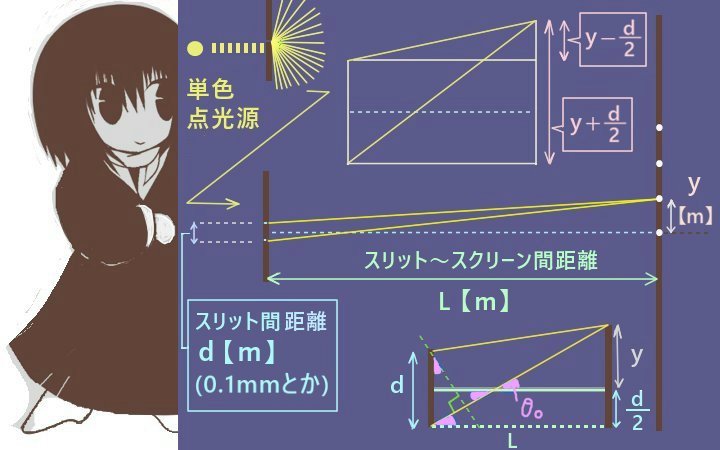
三角比を使う場合

三角比を使う場合は式の構造は単純ですが、図において厳密に成立する関係と近似によってほぼ成立すると見てよいものを区別する必要がある事に注意が必要です。

まず厳密に成立する関係を見るために図の下側のスリットからの光線に注目して、
「スクリーン上の原点とスリット板中央を結ぶ直線」とのなす角をθ０とします。
（あるいはスリット板に垂直な任意の直線とのなす角と考えても同じです。）

ここではθ０とθという２つの角度を考えて、それらが近似的にほぼ等しいとみなせるという形で関係式を導出しますが、最初から２つを同一視して話が進められる事も多いです。得られる結果は同じです。

次に図の下側のスリットからの光線に対して、上側のスリットから垂線を引きます。
その垂線とスリット板とのなす角はθ０に等しくなります。

ここでLが十分大きいとして近似を行います。まず、２つの光線は平行ではありませんが
「ほぼ平行」と考えて光路差はｄsinθ０であると考えます。

さらに２つの光線は平行とみなせるほどになす角が小さいとします。
すると、スリット板中央から「スクリーン上の原点よりｙの距離の位置」に対して引いた直線も２つの光線とほぼ平行と見なせます。

今、θを tanθ＝ｙ／Ｌを満たす角度とすると、上記の近似によりθ０≒θとできるので、
光路差はｄsinθ０≒ｄsinθと書く事ができます。θの値が小さい時にはさらにsinθ≒tanθの近似式も成立するのでｄsinθ≒ｄtanθ＝ｙｄ／Ｌの関係が近似的に成立します。
【cosθ≒０のもとでtanθ＝(sinθ)／(cosθ)≒sinθ】

そこで、スクリーン上で波が強め合う条件としては光路差が「波長の整数倍」になっている事を考えればよいので、ｎを整数として次の関係式を導出できる事になります。

  • ｄsinθ≒ｎλ
  • ｄtanθ＝ｙｄ／Ｌ≒ｎλ
  • ｙ≒ｎλＬ／ｄにより、Δｙ＝λＬ／ｄ
    【Δｙ＝(ｎ＋１)λＬ／ｄ－ｎλＬ／ｄ＝λＬ／ｄ】
    【単純にｎ＝１の時を考えてΔｙ＝λＬ／ｄとしても同じです。】
  • λ＝Δｙｄ／L

以上の方法は、近似を認めるなら非常にシンプルで分かりやすいとも言えますが、肝心の近似が本当に成立するのかが図だけからは分かりにくい（図では説明の都合上、拡大して描かれる事が多いので）という事も同時に言えるかもしれません。

上記の近似を本当にしてもよいのかという事に関する考察は平面幾何的に考える事も可能ですが、次に見て行く光路差の別の導出方法から計算される結果の一部を使って後述する事にします。

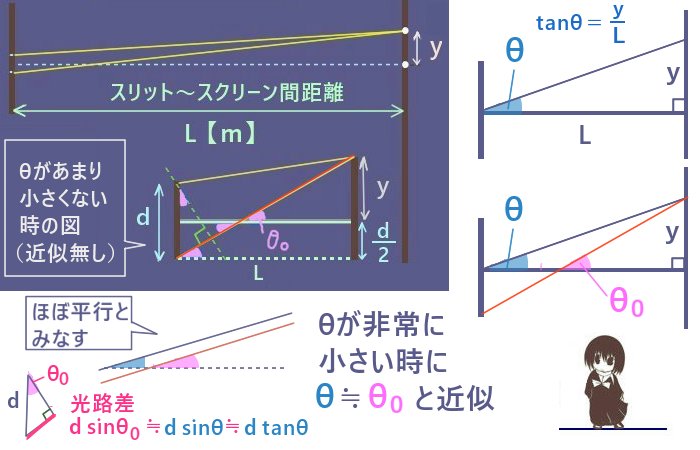
この図では２つの角度を分けて記していて、両者はスリット～スクリーン間の距離が十分大きい条件下で近似的には「ほぼ同じ」とみなせます。他方で、その近似を最初から行うと考える場合もあり、図でも２つの角度を同一視して説明がなされる事があります。

また、この時に sinθ≒θである事もよく強調されます。（θは弧度法での角度とします。）
これはマクローリン展開からsinθ＝θ－θ３／(３！)＋θ５／(５！)－・・・
と書けるので、θが０に近い値の時にはベキ乗の項は全て０に近似できるとするものです。
例えばθ＝０.０１であればθ３／(３！)＝０.００００００１６６・・・となるので、
θ＝０.０１に対して「ほぼ無視できる」
（測定の結果にほぼ無影響と考えてよい）とするわけです。
あるいは、θ＝０における正弦関数の微分係数は１であるので、θが０に近ければ
近似１次式として１・θ＝θがsinθに非常に近い値になると考える事もできます。
また余弦に関してはcosθ＝１－θ２／(２！)＋θ４／(４！)－・・・が成立します。
ここで先ほどと同じように例えばθ＝０.０１の時には
cosθ≒１－０.００００２５＋・・・≒０９９９９７５なので、
tanθ＝(sinθ)／(cosθ) の関係から
θが小さい時のtanθ≒sinθの近似式も成立しているとみてよい事が分かります。

一般二項定理で平方根を展開する方法

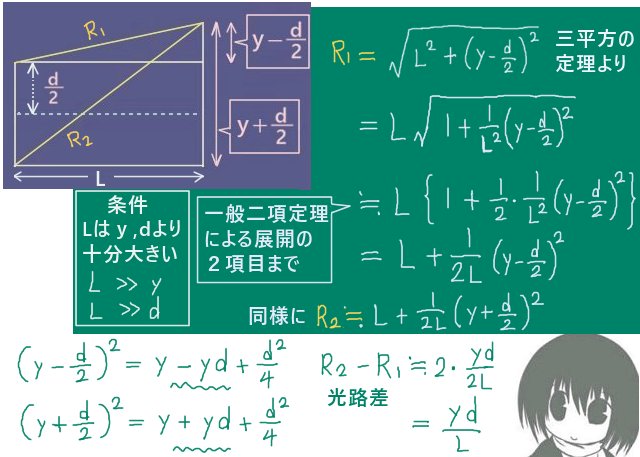
光路差を計算方法としては、平方根を展開して直接計算するというものもあります。

まず近似のない状況下で三平方の定理によって２つの光路の大きさを計算しておきます。それは平方根を使って書けるわけです。

次に少し式を変形してから、
(１＋Ｐ)１／２の形の式に対する一般二項定理による展開を使って光路の大きさを表す式を変形します。（マクローリン展開と考えても同じです。）

近似を使うのはそこからで、ｙやｄに対してＬが十分大きいという条件から展開式の第３項以降は０に近い数値であるとみなす事で、式が簡単になります。

それから光路差を丁寧に直接計算（単純な引き算）すると、光路差がほぼｙｄ／Ｌ（≒tanθ）に等しいという事を導出できます。波が強め合う条件から波長を含んだ関係式を作るのは三角比を使った導出の時と同じになります。

具体的な計算は次のようになります。
２式の違いは、ｙ－ｄ／２を考えるかｙ＋ｄ／２を考えるかの所だけです。

図の上側のスリットからの光路の長さ\(\sqrt{L^2+\left(y-\frac{\Large d}{\Large 2}\right)^2}=L\sqrt{1+\frac{\Large 1}{\Large L^2}\left(y-\frac{\Large d}{\Large 2}\right)^2}\)
図の下側のスリットからの光路の長さ\(\sqrt{L^2+\left(y+\frac{\Large d}{\Large 2}\right)^2}=L\sqrt{1+\frac{\Large 1}{\Large L^2}\left(y+\frac{\Large d}{\Large 2}\right)^2}\)

これらを一般二項定理で展開します。(１／L) (ｙ－ｄ／２)＝ｙ／Ｌ－ｄ／(２Ｌ)が０に近い値である条件のもとで ３項目以降はほぼ０と考えて、２項目まで残したものに近似すると次のようになります。

図の上側のスリットからの光路の長さ\(L\sqrt{1+\frac{\Large 1}{\Large L^2}\left(y-\frac{\Large d}{\Large 2}\right)^2}≒L+\frac{\Large 1}{\Large 2L} \left(y-\frac{\Large d}{\Large 2}\right)^2\)
図の下側のスリットからの光路の長さ\(L\sqrt{1+\frac{\Large 1}{\Large L^2}\left(y+\frac{\Large d}{\Large 2}\right)^2}≒L+\frac{\Large 1}{\Large 2L} \left(y+\frac{\Large d}{\Large 2}\right)^2\)

光路差はマイナスの値になっても別に構わないのですが、分かりやすさのために下側の光路の長さから上側の光路の大きさを引く事で光路差を計算すると次のようになります。光路差が波長の整数倍であるとおけば光が強め合う位置での関係式が導出されます。

光路差
の近似式		\(\left\{L+\frac{\Large 1}{\Large 2L} \left(y+\frac{\Large d}{\Large 2}\right)^2\right\}-\left\{L+\frac{\Large 1}{\Large 2L} \left(y-\frac{\Large d}{\Large 2}\right)^2\right\}\)
\(=\frac{\Large 1}{\Large 2L}\left(2\cdot\frac{\Large yd}{\Large 2}\right)-\frac{\Large 1}{\Large 2L}\left(2\cdot\frac{\Large -yd}{\Large 2}\right)=\frac{\Large yd}{\Large L}\)
波が強め合う
条件		\(\frac{\Large yd}{\Large L}=n\lambda\)，　\(\frac{\Large \Delta y d}{\Large L}=\lambda\)【三角比を使って導出した時と同じ】

この導出方法だと、途中計算が少し複雑に思える部分もあるかもしれませんが、ｙやｄに比べてＬが十分大きい時にどの項を０に近似しているかが比較的明確になるとも言えます。

計算でたくさん「２」が出てきてややこしいですが、丁寧に計算すると光路差について三角比を使った時と同じ近似式を導出できます。
一般二項定理とここでの使い方

(ｘ＋ｙ)aに対する二項展開は指数が任意の実数値でも自然数の時と同じ形の式として書く事ができて次式のようになります。（一般的には無限級数です。）
■一般の式
【厳密には、a が自然数でない時には式が収束する事が保証されるのは(１＋P)a の形で|P|＜１の時なので、一般の場合には式変形をしてその形にする事が必要。】 $$(p+q)^a=p^a+ap^{a-1}q+\frac{a(a-1)}{2!}p^{a-2}q^2+\frac{a(a-1)(a-2)}{3!}p^{a-3}q^3+\cdots$$ ■上式で a ＝１／２とした場合は平方根の展開式の１つ $$\sqrt{p+q}=(p+q)^\frac{\large 1}{\large 2}$$ $$=p^{\frac{\large 1}{\large 2}}+\frac{1}{ 2}p^{-\frac{\large 1}{\large 2}}q+\frac{\frac{\large 1}{\large 2}\cdot\left(-\frac{\large 1}{\large 2}\right)}{2!}p^{-\frac{\large 3}{\large 2}}q^2+\frac{\frac{\large 1}{\large 2}\cdot\left(-\frac{\large 1}{\large 2}\right)\cdot\left(-\frac{\large 3}{\large 2}\right)}{3!}p^{-\frac{\large 5}{\large 2}}q^3-\cdots$$ $$=p^{\frac{\large 1}{\large 2}}+\frac{1}{ 2}p^{-\frac{\large 1}{\large 2}}q-\frac{1}{8}p^{-\frac{\large 3}{\large 2}}q^2+\frac{1}{16}p^{\frac{\large 5}{\large 2}}q^3-\cdots$$ ■特にｐ＝１かつa ＝１／２の場合の式は次式です。 $$\sqrt{1+q}=(1+q)^\frac{\large 1}{\large 2}$$ $$=1+\frac{1}{ 2}q-\frac{1}{8}q^2+\frac{1}{16}q^3+\cdots$$ ■さらに、qが０に近い値なら次式に近似できます。 $$\sqrt{1+q}=(1+q)^\frac{\large 1}{\large 2}≒1+\frac{1}{ 2}q$$

■さらにｑ＝\(\frac{\Large 1}{\Large L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2\)とした時
\(\sqrt{ 1+\frac{\Large 1}{\Large L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2} =\left\{ 1+\frac{\Large 1}{\Large L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2 \right\}^{\frac{\large 1}{\large 2}} \)
\(=1 +\frac{\Large 1}{\Large 2L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2- \frac{\Large 1}{\Large 8}\frac{\Large 1}{\Large L^4}\left(y\pm\frac{\Large d}{\Large 2}\right)^4 +\cdots【ここで３項目以降は０に近似可能】\)
\(≒1 +\frac{\Large 1}{\Large 2L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2\)
よって、\(L\sqrt{ 1+\frac{\Large 1}{\Large L^2}\left(y\pm\frac{\Large d}{\Large 2}\right)^2} ≒L+\frac{\Large 1}{\Large 2L}\left(y\pm\frac{\Large d}{\Large 2}\right)^2\)

上記では平方根を展開して第２項まで近似した状態で関係式を導出しましたが、
第２項もじゅうぶん０に近いとして近似すれば
斜辺の長さを底辺とほぼ同じ L として考える事もできます。
そこまで近似するとやり過ぎ感もあるかもしれませんが、実際のところは
それが「θが小さい値の時に tanθ≒sinθ」とする近似に他なりません。
【三角比の定義から考えてみてもｂ／a≒ｂ／ｃつまり a≒ｃという近似です。】
上記の計算からは、考えている諸量（L，ｄなど）がどのような値の時にその近似をしてよいかがより具体的に分かるとも言えます。
斜辺を底辺とほぼ同じとみなす近似のもとで
前述の三角比による計算でのsinθ０を数式で書いてみると、$$\sin\theta_0 =\frac{y+\frac{\Large d}{\Large 2}}{L+\frac{\Large 1}{\Large 2L} \left(y+\frac{\Large d}{\Large 2}\right)^2}≒\frac{y+\frac{\Large d}{\Large 2}}{\large L}$$ところで sinθ≒tanθ＝ｙ／Ｌですから、sinθ０≒sinθ≒tanθ＝ｙ／Ｌの近似が成立するには
「ｙに対してｄ／２がじゅうぶん小さい時」
つまりｙ＋ｄ／２≒ｙと見なせる時であると言えます。
実の所それは図で見てもそうであるわけですが、数式的に考えるのであれば例えばこのような方法もあるという事になります。
例えばｄ＝１.０×１０－４【ｍ】，L＝１.０【ｍ】，λ＝５.０×１０－７【ｍ】であれば、
三角比を使わない方法でもΔｙ≒λＬ／ｄの関係式は導出できた事にも注意して
Δｙ≒λＬ／ｄ＝５.０×１０－３【ｍ】なので
「ｎ＝１の時のｙ」(＝Δｙ) とｄ／２は１００倍の大きさの違いという事になります。
これもまた図形的にも見る事ができますが、ｎ＝２，３の時には
ｙの値は２倍，３倍になるのでｙとｄ／２の倍率の違いはさらに大きくなる事が分かります。
以上の計算は考察の方法の１つであり、考え方は他にもあります。

干渉光の強度の式

干渉縞の明線の間隔Δｙは一定値となりますが、ｙが大きくなると光の重ね合わせの「強度」は小さくなっていきます。それに対応する形で、明線の明るさはスクリーン中央で最大であり、中央から離れていく（ｙおよびｎが大きくなっていく）ほどわずかに薄く弱い輝きになっていきます。

光を正弦波で表せると仮定した時、光の強度定量的に表すと次のようになります。

波が正弦波である時の干渉光の強度

正弦波の「強度」は定量的には「波の振幅の２乗」として定義されます。
【振幅の２乗に比例する量として考える事もありますがここではその比例係数を１とします。】
重ね合わさる前のもとの光の振幅がともに A【ｍ】で、
強度もともに等しくA2＝I0であるとすると
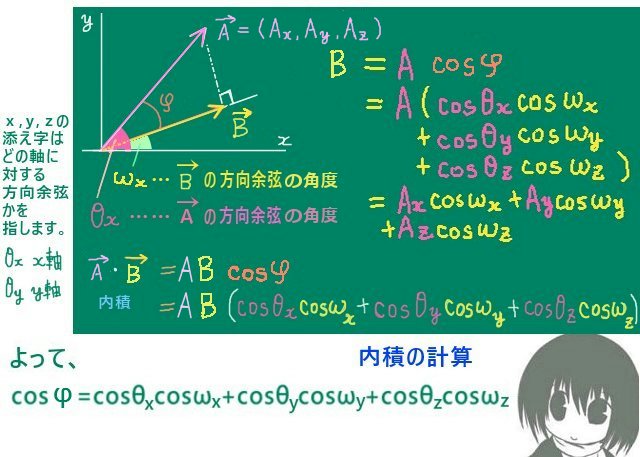
スクリーン上での２つの光の重ね合わせ（「干渉光」）の強度は次式で表されます。 $$I=4I_0\cos^2\left(\frac{\pi yd}{\lambda L}\right)$$ $$=4A^2\cos^2\left(\frac{\pi yd}{\lambda L}\right)$$ｙが増えて行くと余弦の値が小さくなり、強度も小さくなるという計算になります。 この式の余弦の中身は実験で使っている諸量に由来しますが、「余弦自体」は二重スリット実験における図形的な位置関係に由来するものではない事に少し注意が必要です。つまり、二重スリット干渉実験で波長を表す近似式で使っている三角比とは別物です。
強いて表すなら、近似式で使った三角比は強度を表す式の「余弦の中身」に入ります。 $$I=4I_0\cos^2\left(\frac{\pi yd}{\lambda L}\right)≒4I_0\cos^2\left(\frac{\pi d\sin\theta}{\lambda }\right)≒4I_0\cos^2\left(\frac{\pi d\tan\theta}{\lambda }\right)$$

光の波が正弦波であると仮定した時の干渉光の強度に関する式は、この記事内でも少し触れた加法定理による重ね合わせの式から導出できます。すなわち、正弦と余弦の積になった形の式において時間変動を含まない部分を余弦も含めて振幅とみなして２乗する事で上式が導出されます。整理してまとめると次のようになります。

スクリーン上の１つの点で
正弦波で表された２つの光		Asin(kR1－ωｔ)
Asin(kR2－ωｔ)
重ね合わせて加法定理
により得る干渉光の式		\(2A\sin\left\{\frac{\Large k(R_1+R_2)}{\Large 2}-\omega t\right\}\cos\frac{\Large k(R_1-R_2)}{\Large 2}\)
光路差を表す式\(R_1-R_2≒d\tan\theta=\frac{\Large y d}{\Large L}\)
波数の定義\(k=\frac{\Large 2\pi}{\Large \lambda}\)
干渉光の振幅
（時間変動を含まない部分）		\(2A\cos\frac{\Large k(R_1-R_2)}{\Large 2}=2A\cos\left(\frac{\Large \pi yd}{\Large \lambda L}\right)\)
干渉光の強度
（振幅の２乗）		\(4A^2\cos^2\left(\frac{\Large \pi yd}{\Large \lambda L}\right)=4I_0\cos^2\left(\frac{\Large \pi yd}{\Large \lambda L}\right)\)
この干渉光の強度についての式の導出においては、数式的には
波長λは波数の定義から式に入っている事になります。

同じように正弦波で表せる仮定のもと、波動を敢えて複素数で表す場合でも（指数関数表示・極形式による表示では三角関数を含む形になるので）同じ式を導出できます。
その場合には強度は複素数で表した波の絶対値の２乗として定義し、
波を重ね合わせた時の強度は形式的に余弦定理を使った形の式で表されます。
その式において２つの波の振幅は同じであるとして加法定理、半角の公式、倍角の公式のいずれかを適用する事で上記と同じ形の式が得られます。

光源に要求されるコヒーレンス（可干渉性）

ところで、光の二重スリット干渉実験では光源として使用する光の種類についての考察も重要な実験の要素の１つと言えます。

波の干渉を調べる場合、２つ以上の波が強め合うかつぶれて弱め合うかを解析して計算をするにはどこか最初の位置で「位相を同じ値にしておく」という制御が必要です。

その事は、二重スリットの部分においては波の回折を起こさせる事で実現しています。つまり元々位相がそろった波面の波を２つのスリットに進入させる事によって、その２点から進む「同時刻で同位相の２つの光」の光路の長さと波形のずれの関係を適切に計算できるわけです。

他方で、二重スリットに入る光のもとになっている光源の光の種類にも実は注意する必要があります。光の二重スリット干渉実験の光源としては結論としてはレーザー光を使うのが最も好ましいわけですが、逆にそれ以外の光ではだめなのかという話にもなります。

太陽光やいわゆる「白色光」には実は多くの波長の光が混ざっています。
そのため、そのような光をそのまま光源に使って直接的に二重スリットに通しても干渉縞が発生しないか、干渉縞が観測できても上手く測定ができないという事があるのです。

光の干渉実験に白色光を使う場合には
①光源からの光を小さい穴に通して回折を起こさせて位相を揃えた波を作る
②色フィルタ等をおいて単色光に近い光にする
という工夫が必要になります。
もし①だけ行って②を行わない場合、虹のようなたくさんの色の干渉縞が現れます。そのような干渉縞は、測定があまりしやすくない事があります。

光の二重スリット干渉実験にもとになっているのはイギリスの人ヤングによる実験（１９世紀初め頃）で、当時は光源として太陽光を使って光の干渉を確かめる実験が行われたと言われます（当時はレーザー光は利用不可能）。その時に干渉縞はしっかりと確認されて、光の波動性が確認された最初の実験であるとされます。また、残っている講演の資料等によるとヤングは光の干渉を上手く起こすためのコヒーレンシーの考え方（用語自体ではなく）についても当時から指摘していたとされます。

それに対してレーザー光は単色とみなせるほどに波長の幅が小さい光であり、また位相もそろっている光です。レーザー光のように波動（主に光）の位相が揃っている事を指して可干渉性あるいはコヒーレンスと呼び、そのような性質を持った光をコヒーレント光あるいはコヒーレントな光であると分類する事があります。太陽光や白色光は一般的にコヒーレンスを備えていません。

レーザー光線は基本的に人工的に形成される光ですが、光の干渉を調べる時に使う光源としては最適です。重要な特徴を整理すると次のようになります。

  • 単色性：非常に近い値の波長の光だけで構成され、ほぼ単色とみなせる。
  • 可干渉性（コヒーレンス）：位相がほぼそろっている光で構成されており、精度の高い干渉縞を観測可能。単に「干渉性」と言ったり、コヒーレンシーと呼ぶ場合もあります。
  • 指向性（収束性）：長距離を光があまり広がる事がなく進行し、非常に狭い範囲に光を集める（収束させる）事が可能。
  • 高出力性および高輝度性：時間あたりに放出するエネルギーが非常に大きい光（材料加工などに使用）であり得る。光の干渉実験で使うレーザー光は、出力としては弱いものを使用します。

詳しく見ると、コヒーレンス(coherence)には波の位相の波数および位置座標を含む項に由来する「空間的なコヒーレンス」と、角周波数および時間を含む項に由来する「時間的なコヒーレンス」があります。レーザー光は空間的にも時間的にもコヒーレントな光ですが、それが特定の物質を通過して拡散する事で、時間的なコヒーレンスだけを備えた光になるという事もあり得ます。
coherent という語は少し聞き慣れない語かもしれませんが一応普通に使われる語でもあり、密着しているとか結合しているといった意味合いが元々あって、転じて「話や議論の筋が通っている、理路整然としている」 といった意味などとして使われます。

波動の式と用語【正弦波】

恭平

波を表す具体的な形として最も基本的な「正弦波」は関数としては三角関数の正弦関数 sinθですが、波動を表す関数として考える時の変数としては位置座標と時間の両方を考えるのが普通です。

「振動」も波動に関連が特に深い物理現象であり、波動においても個々の位置では振動が起きているとみなせる事もあります。ただしここではバネの振動現象などは除いて、特に波動のほうに注目して見て行きます。

水面の波、あるいは数学では三角関数の sinθのグラフのイメージで上下方向の振動（グラフだとy方向）を特に「変位」と呼ぶ事あり、ここでもその言い方を使います。横に進んでいく方向（グラフだとｘ軸方向）を波が「進行」する方向と呼ぶ事にします。

物理的な「波」の種類

波動は基本的には何かの物質が個々の位置で時間変化により振動していて、その振動が周囲にも伝わっていく事を指します。その振動して波を構成する物質は媒質（「ばいしつ」）と呼ばれます。例えば海の潮の満ち引きの「波」の媒質は水であり、音の場合は基本的には媒質は空気で、水中やそれ以外の物質でも音は伝わるので色々な物質が媒質になり得ます。

他方で「媒質が無くても媒質による波と同じように振る舞うもの」は物理上、普通は「波」として扱われてそのようにも呼ばれる事が一般的です。例えば光（および電磁波）は、実は何かの媒質が直接的に振動しているわけでは無い事が知られています。
また同じく、一般的にミクロのスケールでの量子力学的な「波」は定量的には波動と同じように振る舞うという事を意味し、何かの媒質が直接的に振動しているわけではないという考え方がなされます。（光も、より詳しく見る場合には量子力学的に解析されます。）
他方で正弦波に近い形の電圧である交流電圧は、人工的に起電力をそのような形で発生させ続ける事によって波と同じ関数形として扱うという類のものです。
しかしいずれにしても、数式的に波の形として扱える物理量には、媒質の振動による波動の用語や考え方の多くを適用できます。特に光および電磁波に関しては普通に代表的な波動の現象の１つとして捉えられる事が一般的です。

実際に目で見える波の形や、物理量をグラフとして描いた時の形は波形と呼ばれます。
正弦波の波形はそのまま正弦関数のグラフの形ですが、波形は一般的には他の形状もあります。
例えばグラフ上で長方形状になる波形は
方形波あるいは矩形波【矩形：「くけい」長方形の事。矩とは直角の意味。】などと呼ばれます。
また、一般的に正弦波の波形が微妙に歪んでいたり台形状や三角形状の波形になっている波を総称してひずみ波と呼ぶ事もあり、矩形波等を含めてそのように呼ぶ事もあります。

数学的には、実は正弦波以外の波は周期関数でないものも含めて
「振動数が異なる複数の正弦波の合計（重ね合わせ）」として表現できます。
そのように解析した場合には波を構成する正弦波のうち振動数が最も小さいものを基本波と呼び、残りの物を高調波と呼ぶ事があります。

波動は進行方向に対する振動の向きの方向によっても分類され、一般的に横波と縦波の２つに大別されます。（ただし、数式的に「波として扱える」だけの場合はどちらにも含めない事もあります。）
正弦関数のグラフの形が実際の波の波形として観察できるようなものは「横波」のほうで、水面や弦を伝わる一般的なイメージの波や、光および電磁波は横波に相当します。
横波は、より詳しくは「各位置での振動が波の進行方向に対して垂直である波」を指します。

他方で、ばねを多数連結させた構造や、音波などは「縦波」です。これは、各位置での振動の向きが波の進行方向に対して平行（そして重なっている）である事を意味していて、媒質の密度が大きくなったり小さくなったりを繰り返すので「疎密波」とも呼ばれます。

数式的には縦波も横波と同様に扱う事ができます。
以下では、比較的イメージしやすい横波を想定して説明をしていきます。

また、まずは基本的な考え方となる「進行方向が１次元の波」を正弦波として扱います。（進行方向が１つの軸方向という意味で１次元であり、振動による「変位」も含めれば２次元です。）

波の進行が平面や空間で行われる場合には波の振動の変位が一定となっている波面を想定し、
波面が平面状である平面波や波面が球面状（球対象）である球面波をなどを考えます。
また、平面波において平面電磁波のように波（として扱える物理量）の変位の向きが平面の特定の方向であるものは偏波とも呼ばれます。（光の場合は特に「偏光」とも言います。）
偏波における波の振動の変位の方向が変化しないものは特に直線偏波と呼ばれ、
振動の変位の方向が平面内で変化する場合の偏波を回転偏波と呼ばれる事があります。
さらに細かく見ると回転偏波には特定の規則性を持った円偏波などがあります。

波を構成する物理量

規則的にうねる波を正弦関数で表す事を考える時に、
「波と言ってもどのような波なのか」を表す物理量として次のものがあります。
便宜上ここでは、１回転して元の状態に戻る事をさして「１サイクル」と表現しておきます。

  • 周期：何秒で正弦波が１サイクルするのか
  • 波長：波形で見た時に１サイクルが何メートルあるか（時刻は固定して見た時）
  • 振動数：１秒間で考えた時に何サイクルしているのか。周波数とも言います。
  • 速さ：波形が１秒当たり何メートル進行していくのか。（時間を進めながら位置も見る。）
  • 振幅：波の高さが０から最大値まで何メートルあるのか。

正弦関数 sinθの変数は「角度」です。しかし位置や時刻などの物理量は普通はπの倍数で表しませんから、それを補正して正弦関数に反映されるようにします。

  • 波数：考えている位置や距離が「波長の何倍か」を表す係数です。
  • 角周波数：「１秒当たり角度は何ラジアン進むのか」を表します。角振動数とも言います。回転運動等で使う「角速度」と数式的には同じです。
  • 位相：sinθのθの部分を合成関数になっている場合も含めて特に指す量。
    基本的に弧度法（２πを３６０°とする）で表します。「引数」と呼ばれる事もあります。
    位置座標や時刻は、波数や角周波数を乗じる事によって位相としての量に変換されます。
    「２つの波は位相がπずれている」などと言う場合には角度全体で言うと sinθとsin(θ＋π)の関係である事を表します。普通は位相は０から２πまたは－２πから２πまでの値とします。

また、波のｙ座標方向の値をここでは「変位」と呼んでおきます。

これらに対して多く使われる記号や関係式を整理すると次のようになります。

波動を表す正弦波は A sin (ｋｘ―ωｔ) を基本形として表されます。【あるいはA sin (ωｔ―ｋｘ)】
A：振幅　ｋ：波数　ｘ：位置座標　ω：角周波数　ｔ；時刻　ｋｘ―ωｔ：位相

波動を表す基本的な物理量
物理量記号関係式備考単位
周期TT＝1／f＝λ／vperiod, time period【ｓ】秒
波長λλ＝ｖＴ＝ｖ／ｆwave length【ｍ】メートル
振動数fｆ＝1／T＝v／λfrequency　別名：周波数【Hz】ヘルツ
速さvｖ＝λ／Ｔ＝λｆwave speed 波の進行の速さ【ｍ／ｓ】
振幅色々０からの最大値amplitude 【ｍ】メートル
波数kｋ＝２π／λwave number 1波長で2π【rad／ｍ】
角周波数ωω＝2πf＝2π／T
ω＝ｋｖ		angular frequency
別名：角振動数		【rad／ｓ】
λ「ラムダ」 ω「オメガ」
単位については「ラジアン」の代わりに無単位とする事もあります。
v は速度(velocity) から。通常は速度ベクトルの大きさを「速さ」と呼びます。
振幅の記号は用途ごとに変えるのが普通です。（一般論ではAが多い。）
光に対しては振動数をν（ニュー）で表す事もあり、光の速さはｃで表します。

波動を正弦波として考える時には基本的に角度を弧度法で扱います。すなわち円周率πの何倍であるかで正弦関数の変数を表して、２π で１サイクルして０の時と同じ関数の値に戻ると考えます。

物体の位置関係や傾き具合を三角比として表すような場合であれば、
物理現象を表す時でも「斜面に対して４５°の傾きなので cos45°を乗じて・・」といった表現でも全く支障は無いと言えます。
しかし波動や振動においては周期関数としての三角関数を扱う必要がある事に加えて、
微分や積分を行う観点からも三角関数の位相部分を弧度法で扱っていく必要があります。
例えばｙ＝A sin (ｋｘ―ωｔ)をｘやωで偏微分すると
合成関数の微分（ここでは１変数の時と同じ）となるので
(∂ｙ／∂ｘ)＝ｋA cos (ｋｘ―ωｔ)
(∂ｙ／∂ｔ)＝－ωA cos (ｋｘ―ωｔ)
のような計算になりますが、
もし位相の部分を度数法で表していたら同じ計算にはなりません。
そのため物理学の中でも特に波動や振動を扱う時には、三角関数の角度は度数法ではなく弧度法で統一的に表す事が理論的にも重要であると言えるわけです。
※合成関数に対する偏微分の一般式は、ここでは不要ですが項が１変数の時よりも増えます。

周期と振動数の関係

振動数の単位には普通【Ｈｚ】（「ヘルツ」）を使いますが、
これは無単位（正確には「１」）を秒で割った【／ｓ】にも等しいものです。

周期と振動数の関係T＝１／ｆについては、
例えば１秒間に５０サイクルの振動を繰り返す場合には
１サイクルあたり０．０２秒という事になり、
これは５０【Ｈｚ】の振動数に対して
１／５０＝０．０２【ｓ】という計算をしているわけです。

T＝１／ｆという事はTｆ＝１が必ず成立する事を意味しますが、
Ｔは「１サイクルするのにＴ秒かかる」事を意味し、
ｆは「１秒間にｆサイクルする」事を表すので
要するにTｆ＝１は「Ｔ秒間で１サイクルする」という事を表します。
先ほどの具体例で言うと５０【Hz】の振動数のもとでは１秒間に５０サイクルですから、
１サイクルあたりの時間（＝周期）は０．０２【ｓ】です。
その時間あたりに１サイクルするという関係式が
０．０２【ｓ】×５０【／ｓ】＝１というわけです。

振動数は、波の速さと波長との関係ｆ＝ｖ／λもあります。意味は「１秒間に進む距離は何波長分か」という事で、それは１秒間あたりに何サイクルしているかに等しくなるわけです。

周期は振動数の逆数なのでＴ＝λ／ｖとなります。これは１サイクルの波長に対して何秒で進行できるかを表し、それは１サイクルに要する時間である周期に等いというわけです。

波の進行方向の速さｖは、進行方向（ｘ軸）に向かって同じ変位（ｙ座標）の部分が進んでいく速さを表します。「ｙ方向の変位の速さ」はまた別物となります。

また、後述する角周波数がω＝２π／Tである事からT＝２π／ωです。
その事はｙ＝A sin(ｋｘ－ωｔ)の正弦波があった時に角周波数だけｎ倍したｙ＝A sin(ｋｘ－ｎωｔ) は周期が１／ｎ倍となっている事を意味します。

光や音波は一定の条件下で一定であるかほぼ一定とみなせるので、
その場合は振動数と波長は反比例の関係にあります。
光や音波の性質は振動数で大きく決まります。紫外線などの光や「高い音」は振動数が大きくて波長が短く、逆に赤外線などの光や「低い音」は振動数が小さくて波長が長い波動となっています。
可視光で言うと紫色の振動数が大きく、青、緑、黄色と小さくなって赤が振動数が一番小さい領域です。波長では逆に赤のほうが紫よりも大きくなります。
さらにより詳しく見ると一般的に振動数が高い波動ほどエネルギーが高く、紫外線などの振動数が高い光はエネルギーが高い光でもあります。

正弦波の波長

波の波長は基本的には時刻を固定した時の、
進行方向に対する「１周期分の波の長さ」を測ったものと言えます。

位置や距離を位相に換算する波数がｋ＝２π／λで表され、
位置座標に由来する位相の部分はｋｘで表されます。
１周期分の距離（＝波長）は２πに換算されます。
波長の１／２の「半波長」であればπに換算されるという計算です。

ただし時間を動かした時にも波長を考える計算はできます。
例えば波の進行の速さが２００【ｍ／ｓ】である時、
１周期が０．１秒であるなら「１秒間に２００メートル」は１秒が１０周期分です。
つまりこの時、１周期分の０．１秒あたりは２０メートルの進行があります。
さらに波の振動方向も見るとその間に１サイクルの振動が完了しているわけで、
進行方向の長さは波長です。
これは２００【ｍ／ｓ】×０．１【ｓ】＝２０【ｍ】という計算です。

もし１周期が４秒だったら、波長は２００【ｍ／ｓ】×４【ｓ】＝８００【ｍ】です。

これらの計算が「波長、速さ、周期の関係」を表すλ＝ｖＴの関係の意味です。
周期の代わりに振動数を使えばλ＝ｖ／ｆの関係になります。

もし光のように一定条件下で速さが常に一定であると考えられる場合にはλ＝ｃTであり、波長と周期は比例関係にあります。（ｃは非常に大きい値なので短い周期でも波長は長くなり得ます。）

波の波長は、波同士を重ね合わせた時の波の干渉を分析する時に重要な量です。同じ物理量で表される２つの波が微妙に位相がずれた状態で重ね合わさると、波長の整数倍だけずれていると波は強め合い、波長の整数倍に半波長が加わると弱め合うという現象が起きます。
光が波動であるという実験的な根拠は、光に対して波の干渉が起きるという事（ヤングによる実験）です。（光は同時に粒子でもあります。その粒子が多数集まった時に波動性を表すようになります。ただし粒子同士が相互作用して波になっているという事では無く、より量子力学的な現象としてです。マクロなスケールでは光の波動性は電磁波としても扱われます。）

正弦波の速さ

波動が生じている時、
媒質は各位置で上下に振動しているだけだったとしても
見た目は波形が横に進行していくようにも見えます。

波の速さとは、そのような「波形が移動していく速さ」を指します。
波長および周期との関係式があり、λ＝ｖＴおよびλ＝ｖ／ｆが成立します。

そのため、質量を持った媒質の一部分に対して運動方程式を考えるような時には加速度はあくまで媒質の変位方向（波の進行方向に対して垂直方向など）を考える必要がある場合もあります。

時刻がｔ＝０の時に波形がｙ＝A sin(ｋｘ)で表されている正弦波が、
速さｖでｘ軸方向に移動しているとすると
一般の時刻ｔではｙ＝A sin{ｋ(ｘ―ｖｔ)}＝A sin{２π(ｘ／λ―ｖｔ／λ)}で表されます。
【sin(ｋｘ－ｖｔ)ではない事に注意。ｖｔメートル進むのはx軸での距離です。】

しかし正弦波の基本形はｙ＝A sin(ｋｘ―ωｔ)であったはずです。
すると速さを考える時にはそれとは違った形になってしまうのか？というと、実はそうでは無く
ω＝２π／T＝２πｖ／λによりωｔ＝２πｖｔ／λとなるので、
A sin{ｋ(ｘ―ｖｔ)}＝A sin (ｋｘ―ωｔ)の関係があります。

もう少し詳しく見ると波動において進行方向の速さがｖであるという事は、
１つの時刻を固定した時に（例えばｔ＝ｔ０と指定）
ｘを変数とする２つの関数ｆ(ｘ)とｇ(ｘ)があって、
ｆ(ｘ)＝ｇ(ｘ＋ｖｔ)が任意の位置ｘと時間ｔに対して成立する事を指します。
この関係式は「波がｖｔ【ｍ】進行した」という事を見やすい式です。
しかし、ではその時にｙ＝ｇ(ｘ)はどのような関数形かというと、
ｘ＝Ｘ＋ｖｔとおくと、ｆ(Ｘ)＝ｇ(Ｘ＋ｖｔ)ですが
Ｘ＝ｘ－ｖｔなのでｆ(ｘ－ｖｔ)＝ｇ(ｘ)であり、
「ｙ＝ｆ(ｘ)をｘ軸方向にｐだけ平行移動した関数ｙ＝ｇ(ｘ)はｇ(ｘ)＝ｆ(ｘ－ｐ)で表される」
という関数とグラフ上の平行移動についての一般的な関係式が得られます。
図形的にも物理的にも、ｙ＝Asin(ｋｘ)の波形全体がx軸のプラス方向に移動する時には
まず最初にｘ＝０の位置においてｙの値は小さくなっていきます。
関数は正弦関数ですから位相の値も０の状態からまず小さくなっていくわけで、
ｙ＝Asin(ｋｘーωｔ)におけるーωｔの項の意味を表しています。

ある正弦波ｙ＝A sin(ｋｘ―ωｔ)があってその進行方向を進行波として基準に考える時、同じ波形と物理量を持って「進行の向きだけが逆向き」の波はｙ＝A sin(ｋｘ＋ωｔ)で表され、反射波と呼ばれます。（物理的に見て、そのような波は多くの場合にどこかの端で反射して戻ってくるものなので。）

反射波のほうの式をｖを使って書く事を考えると、
ここでは後述するω＝ｋｖの関係式を使う事にして
ｙ＝A sin(ｋｘ＋ωｔ)＝A sin(ｋｘ＋ｖｋｔ)＝A sin {ｋ(ｘ＋ｖｔ) } であり、
ｙ＝A sin(ｋｘ) の波形全体を「ｘ軸のマイナス方向にｖｔだけ平行移動させた関数」に一致します。

角周波数

角周波数あるいは角振動数ωは、ωｔの形で位相の時間部分を表す量です。

「角速度」（angular velocity）は回転運動を表すのに使う量ですが１秒間あたりの角度の変化量という意味では角周波数と同じであり、記号も同じωを使う事が多いです。
ただし角速度は波動以外の一般の運動に対して使う量ですから、波動における関係式は一般的には成立しません。

ω＝２π／Ｔは、１周期分の時間で位相がπになるようにする換算の計算です。
例えばある時刻から０．５周期分だけの時間が経っているなら位相の変化（「位相差」）は
ωｔ＝（２π／Ｔ）×０．５Ｔ＝πとなる計算です。

ω＝２πｆの関係式も成立します。
例えば５０【Ｈｚ】の振動数に対しては１秒間あたり１００πの位相差が生じる事を意味します。
（※ただしその場合は１００πは２πの整数倍ですから位置を固定すれば正弦関数の値は変化せず、実質の位相差は０と同じです。）
０．０１秒間ではωｔ＝２πｆｔ＝１００π×０．０１＝πの位相差が生じる計算になります。

基本となるA sin (ｋｘ―ωｔ)の形を見ると波数ｋと角周波数ωは一見全く別々の物理量かとも思えるわけですが、速さｖによってｋとωの関係式を作れます。
ｋ＝２π／λで、ω＝２π／Ｔ＝２πｖ／λなのでω＝ｋｖの関係が実はある事が分かります。

時刻を固定してから波の進行を考えてA sin (ｋｘ－ωｔ)の形を導出できるのと同様に、最初に位置を固定して時間による振動から考える事もできます。

ｔ＝０の時にｘ方向に関してはsin (ｋｘ）の波形があるとします。
この時に波がプラス方向に進行する時にはｙ方向の変位はｘ＝０においてマイナス方向に現れ始めるので、敢えて「ｘ＝０でA sin (－ωｔ)の振動がある」と考えます。

プラスの値のｘの位置で
「ｘ＝０の時と同じｙの変位が現れる時刻」は波の速さを考慮してｘ／ｖ秒後です。
よって、任意のｘの位置における振動はω＝ｋｖの関係式も使って
ｙ＝A sin {－ω(ｔ－ｘ／ｖ)}＝A sin (－ωｔ＋ωｘ／ｖ)＝A sin (ｋｘ―ωｔ)の形を得ます。

波数と平面や空間での波数ベクトル

波数はｋ＝２π／λで表され、速さｖを使うとｋ＝２π／(ｖＴ)＝ω／ｖとも表せます。

いずれにしても意味としては
「１波長分（１周期分）がいくつ含まれているかを位相に換算する量」という事になります。

平面や空間では、波の進行方向を表すベクトルとして波数ベクトルが使われる事があります。

波数ベクトルの表し方はいくつかありますが、
その１つは個々の位置での波の進行についての速度ベクトルを使う方法です。

速度ベクトルを(ｖ１，ｖ２，ｖ３)として、その大きさ（速さ）をｖとします。
すると、速度ベクトルを「大きさが１である」単位ベクトルにした
(１／ｖ) (ｖ１，ｖ２，ｖ３)というベクトルを考えると
これは各点において波の進行方向を向く単位ベクトルです。

それにｋを乗じたものを波数ベクトルとして考える事ができます。
すなわち、\(\overrightarrow{k}\)＝(ｋ／ｖ) (ｖ１，ｖ２，ｖ３)として考えます。
波数ベクトルの大きさは波数ｋに等しくなります。

特に平面波では同じ位相の平面が波を作っており
それらの平面間の距離によって位相差が決まるので、
原点から個々の点（ｘ，ｙ，ｚ）から波の進行方向への射影を図形的に考えると距離の変化による位相の変化は波数ベクトルとベクトル（ｘ，ｙ，ｚ）の内積で表す事ができます。
【原点を通る波面は必ず存在し、平面波においてその波面上での位相は等しいので統一的に波面と波面の位相差を「距離に波数ｋを乗じる」という式で表す事ができて、さらにそれは波数ベクトルを使うと内積により表現可能であるという事です。】

波数ベクトル

波の進行についての各点での速度ベクトルを\(\large{\overrightarrow{v}=(v_x,v_y,v_z)}\)として、
その大きさをｖとすると 波数ベクトルは次式で表されます。 $$\overrightarrow{k}=k\frac{\overrightarrow{v}}{v}$$ $$\left|\overrightarrow{k}\right|=k=\frac{2\pi}{\lambda}$$ ■特に空間内の平面波において各点の変位 u(x,y,z,t) を正弦波で表せる場合には、
\(\large{\overrightarrow{r}=(x,y,z)}\)として次式が成立します。 $$u(x,y,z,t)=A\sin\left(\overrightarrow{k}\cdot\overrightarrow{r}-\omega t\right)$$ ωｔの部分は進行方向が１次元の場合と同じです。
また、平面波であれば実は正弦波でなくても
より一般的に \(u(x,y,z,t)=f\left(\overrightarrow{k}\cdot\overrightarrow{r}-\omega t\right)\)と表す事が可能です。

波を正弦ではなく余弦で表す事と「位相のずれ」の関係

ところで正弦波を通常の三角関数として考えた時に、正弦ではなくて余弦で表してもよいのではないか？と思われるかもしれませんが、実際その通りで正弦波で表される波は余弦関数で表しても何ら支障はありません。

つまりｙ＝A cos (ｋｘ―ωｔ)として波を表してもよいわけです。

ただし同じ物理量の波を正弦波で表した場合との関係には注意するべきで、
ｙ＝A cos (ｋｘ―ωｔ)＝A sin (ｋｘ―ωｔ＋π／２)の関係があります。
ｙ＝A sin (ｋｘ―ωｔ)とｙ＝A cos (ｋｘ―ωｔ)との間には位相差があって、２つの関数を同時に使う時は正弦と余弦の関係からも分かるように同一の関数ではありません。

また同様に、正弦波をｙ＝A sin (ｋｘ―ωｔ)ではなくｙ＝A sin (ωｔ―ｋｘ)で表したとしてもそれ自体は波動の現象を考察するうえで基本的に問題は無いわけですが、やはり同じくｙ＝A sin (ｋｘ―ωｔ)の波とは位相のずれがあり、
ｙ＝A sin (ωｔ―ｋｘ)＝A sin (ｋｘ―ωｔ＋π)＝の関係があります。
今度は位相のずれはπになっているわけです。
【＋πを－πとしても同じです。三角関数は２πを周期とするためです。
ｙ＝A sin (ωｔ―ｋｘ)＝―A sin (ｋｘ―ωｔ)に等しいと見る事もできます。】

ｙ＝A sin (ｋｘ―ωｔ)は、より正確には定数θ０を使って
ｙ＝A sin (ｋｘ―ωｔ＋θ０)の正弦波でθ０＝０としたものです。
【通常はそれで問題は起きません。】
ｘ＝０，ｔ＝０の時の値がｙ＝A sinθ０となります。
そしてそのθ０は必要があればπ／２でもπでもよいわけで、
そのような場合には波はｙ＝A sin (ｋｘ―ωｔ＋θ０)は
A cos (ｋｘ―ωｔ)やA sin (ωｔ―ｋｘ)に直接的に変形できます。
言い換えるとｘ＝０，ｔ＝０の時のｙ＝A sinθ０の値の設定次第で、
あるいは現に存在する波に対して
「進行方向のどこを原点にとっていつを時刻ｔ＝０に設定するか」により
A sin (ｋｘ―ωｔ)，A cos (ｋｘ―ωｔ)，A sin (ωｔ―ｋｘ)の形は実は自由に選べるわけです。

このグラフ上で正弦で表した式の位相にπ／２を加えると、
ｋ＝２π／λなのでｋｘ－ωｔ＋π／２＝ｋ(ｘ＋λ／４)－ωｔとなり、
ｘ軸のマイナス方向にλ／４【波長の１／４】だけもとの波形を平行移動させた形になっています。
正弦波の位相にπを加えた時は、同様にして
ｘ軸のマイナス方向にλ／２だけもとの波形を平行移動させた形になっています。

正弦波の位相の表し方の整理

正弦波ｙ＝A sin (ｋｘ―ωｔ)において位相の形ｋｘ―ωｔを見ると、位置座標と時刻の両方が変数になっています。つまり、同じ位置で時間による変動を見てもよいし、時刻を固定して波形の様子を見る事もできるようになっています。

つまり、いずれにしても位相に対する正弦関数の値として統一的に波の様子を表現できるようになっているわけです。

この事は、時刻を固定してｘ軸とｙ軸の関係でグラフを正弦関数として描けるだけでなく、位置ｘを固定して時刻ｔとｙ軸の関係におけるグラフも同じく正弦関数として描ける事を意味します。なぜならばどちらを変数としても、もう片方を固定すればｙ＝A sin θの形の関数になっているためです。

正弦波の位相部分に対してはｋ＝２π／λ，ω＝２π／Ｔの関係を使って
ｙ＝A sin (ｋｘ―ωｔ)＝A sin {２π(ｘ／λ―ｔ／T)}のように書く事もできます。
これは関係式を使って書き直しただけと言う事もできますが、
「位置や距離が波長の何倍か」「時刻や時間が周期の何倍か」で位相の変化を考えている事をより明確にするならこのようになるという事です。
もちろん、同じ意味をより簡潔に記せばｙ＝A sin (ｋｘ―ωｔ)であるわけです。

さらに振動数ｆなどを使って書く事もできて、整理すると次のようになります。

使用する物理量の例正弦波の位相備考
ｋ，ωｋｘ―ωｔ基本形【ωｔ－ｋｘでも可】
λ，T２π(ｘ／λ―ｔ／T)位置は波長の何倍か、
時間は周期の何倍かで位相を見る
λ，ｆ２π(ｘ／λ―ｆｔ)時間を２πが何個分かで見る
ｖ，Ｔ，λ２π{ｘ／(ｖT)―ｖｔ／λ }λ／ｖ＝Tよりλ＝ｖT，
１／T＝ｖ／λ
ｋ，ｖｋ(ｘ―ｖｔ)ｘ軸方向にｖｔ平行移動した形
【ｋｘ―ωｔに等しい】
ω，ｔω(ｘ／ｖ－ｔ)ｘ＝０での振動から考えるか、
ω＝ｋｖの関係から

単位を利用した関係式の理解の仕方【次元解析】

波動に関する物理量の関係式は基本的ないくつかの式（T＝１／ｆなど）を除くとそもそも覚え込むような性質のものではありませんが、それにしても分母と分子の関係がごっちゃになったりする事もあるかもしれません。微積分の計算等とはまた違った難しさがあると言えます。

そこで、あくまで補助的なものである事は強調されるべきかと思いますが、単位の関係を利用して理解に役立てたり、関係式を思い出す際に混乱した時などに使える事があります。
（物理では「次元解析」とも言います。この「次元」とは平面を２次元、空間を３次元と呼んだりする「次元」とは直接的には無関係です。）

例えばλ，ｖ，Ｔの関係を考えてみましょう。
これらの単位はそれぞれ【ｍ】【ｍ／ｓ】【ｓ】です。
すると、もし例えばλｖとかｖ／Ｔといった値を考えるとそれらの単位は【ｍ２／ｓ】とか【ｍ／ｓ２】（後者は加速度の単位）といったものになってしまいますが、いずれもλ，ｖ，Ｔの単位に該当せず、波動に関する他の物理量の単位にも当てはまりません。

すなわちλｖとかｖ／Ｔといった量は少なくとも基本関係式で使う事は無いという判断が可能であるとも言えるわけです。

もし関係式を忘れてしまって必要なのに急に思い出せないとして、
単位の関係からλ，ｖ，Ｔに対して成立する正しい関係式を推測するとしましょう。

すると、【ｍ】と【ｓ】から【ｍ／ｓ】が作れるはずであり、
λ【ｍ】／T【ｓ】＝ｖ【ｍ／ｓ】の関係が推測できます。実際、それは正しい関係式になっています。
同じように単位の関係だけからＴ【ｓ】＝λ【ｍ】／ｖ【ｍ／ｓ】の式を推測しても
実際にＴ＝λ／ｖは正しい関係式です。

続いて、λ【ｍ】＝ｖ【ｍ／ｓ】Ｔ【ｓ】の推測からもλ＝ｖＴも正しい関係式を得ます。
λ＝ｖＴの式の右辺についてｖＴなのかｖ／Ｔなのか混乱した時には
単位として【ｍ】となる前者が正しく、
【ｍ／ｓ２】すなわち加速度の単位になる後者は波長λを表す量としてあり得ない事を判定できます。

同様に、前述の波動に関する物理量の関係式は単位の関係からも理解可能です。
（下表で、振動数の単位は【Hz】ではなく【／ｓ】で書いています。）

物理量関係式次元解析による理解の補助
周期T＝1／f
T＝λ／v		【ｓ】＝１／【／ｓ】
【ｍ】／【ｍ／ｓ】＝【ｓ】
波長λ＝ｖＴ
λ＝ｖ／ｆ		【ｍ】＝【ｍ／ｓ】・【ｓ】
【ｍ】＝【ｍ／ｓ】／【／ｓ】
振動数ｆ＝1／T
ｆ＝v／λ		【／ｓ】＝１／【ｓ】
【／ｓ】＝【ｍ／ｓ】／【ｍ】
速さｖ＝λ／Ｔ
ｖ＝λｆ		【ｍ／ｓ】＝【ｍ】／【ｓ】
【ｍ／ｓ】＝【ｍ】・【／ｓ】
波数ｋ＝２π／λ
ｋ＝２π／(ｖＴ)
ｋ＝ω／ｖ		【rad／ｍ】を基本形として、
【rad／ｍ】＝【rad】／（【ｍ／ｓ】・【ｓ】）
【rad／ｍ】＝【rad／ｓ】／【ｍ／ｓ】
角周波数ω＝2πf
ω＝2π／T
ω＝ｋｖ		【rad／ｓ】を基本形として、
【rad／ｓ】＝【rad】／【ｓ】
【rad／ｓ】＝【rad／ｍ】・【ｍ／ｓ】

このような関係は単に式を覚えやすくなるという事に留まらず、物理学一般において異なる物理量の関係を調べる時に整合性がとれてるかの確認等を含めて考察の対象になる事があります。

また、物理量の単位というのは「１秒当たりに何メートル進むか」を【ｍ／ｓ】で表すといったように、それ自体に物理的な意味が含まれている事もあると言えます。
λ＝ｖＴの関係では速さに時間を乗じているから距離となるわけで、
そこに波動現象に特有の１サイクルあたりという意味が加味されるわけです。

物理的な意味（図的な意味も含めて）や数式的な意味に加えて、単位を使った理解の仕方も補助的に知っておくと便利な事があります。

波動方程式の解としての正弦波

一般的に、波動を表す式は次の波動方程式の解として得られます。

波動方程式

u(x，y，z，t)に対する次の微分方程式は波動方程式と呼ばれます。 $$\nabla^2u=\frac{1}{v^2}\frac{\partial^2 u}{\partial t^2}$$ $$\nabla^2=\frac{\partial^2 }{\partial x^2}+\frac{\partial^2 }{\partial y^2}+\frac{\partial^2 }{\partial z^2}$$ 右辺の定数項の分母でｖの文字を使っていますが、
実は波動方程式の解から得られる波動の速さはこの式中のｖで表されます。
▽の記号はナブラと言います。

正弦波の式は１次元の場合の波動方程式の解の１つとなっています。
【ただし解の「１つ」であって、解の全て（一般解）ではありません。】
１次元の場合は関数に対するｙの偏微分、ｚの偏微分は０であるとして波動方程式は、
対象の関数をｙ＝ｙ(x，ｔ)を使って次式になります。

$$\frac{\partial^2 y}{\partial x^2}=\frac{1}{v^2}\frac{\partial^2 y}{\partial t^2}$$

ｙ＝Asin(ｋｘ－ωｔ)がこの式の解であるかどうかは実際に偏微分を行う形で確認できます。
合成関数の微分（１変数）に注意して計算をまとめると次のようになります。

ｙ＝Asin(ｋｘーωｔ)ｘによる偏微分ｔによる偏微分
偏微分１回目ｋAcos(ｋｘ－ωｔ)－ωAcos(ｋｘ－ωｔ)
偏微分２回目－ｋ２Asin(ｋｘ－ωｔ)－ω２Asin(ｋｘ－ωｔ)

ｔによる偏微分の２回目では、cos の微分由来のマイナスと－ωｔの微分由来のマイナスの２つが乗じられるので結果的に符号は１回目の偏微分の時から変わらない事になります。

∂２ｙ／∂ｘ２と∂ｙ２／∂ｔ２の計算結果を見比べてみると、
∂２ｙ／∂ｘ２＝(ｋ／ω)２(∂ｙ２／∂ｔ２) となっています。

つまり、ｖ＝ω／ｋ であると考えると確かに上記の波動方程式を満たしています。
さらに、波の関係式においてω＝ｖｋでしたから波動方程式を満たす定数としての
ｖ＝ω／ｋは正弦波の進行の速さのｖと同一の量である事を確認できます。

直交曲線座標系の成分にベクトルを変換する方法

恭平

物理学などでは、微分方程式を座標変換して考える時があります。
例えば極座標における運動方程式や波動方程式を考えてみるといった事です。

そのような場合で特にベクトルを含む微分方程式を考える時には、
ｘ＝ｒcosθ等の関係の代入だけでなくベクトルの基本ベクトルを変更する事まで行う事があります。
普通はベクトルを成分で表す時には（ｘ座標，ｙ座標，ｚ座標）で考えるわけですが、
それを（ｒ座標，θ座標，φ座標）で表す事を意味します。
例えば運動方程式であれば加速度ベクトルや力ベクトルをそのように扱うという事です。

以下、微分も使いながら具体的な変換の方法などを詳しく説明します。

■この記事に特に関連が深い数学的な事項は方向余弦に関する内容と、極座標および球面座標に関する内容です。その他、記事の後半では微分に関する基本公式のいくつかを使用しています。ベクトルと三角関数に関する基本的な事項も使います。

基本ベクトルの変更をする必要がある場合と無い場合

極座標変換等をする場合の微分方程式については、
基本ベクトルを変更する必要がある場合と無い場合があります。

まず、変更の必要が無い場合を見てみましょう。

例えば「等速円運動をしている物体には常に中心力が働いている」という事を
運動方程式を使って示そうとするような場合です。
この時には物体の座標に対して極座標変換を行ってから時間微分を２回行って、
普通に運動方程式に当てはめて力ベクトルを計算する事には何の問題もありません。
このような場合は、極座標変換を使っていても基本ベクトルの変更が必要ない場合です。

少しややこしいようですがそのような場合には、
「ｘ＝ｒcos(ωｔ) のような極座標変換は確かに行ってはいるけれども、
ベクトルの座標成分としては直交座標によるものを考えている」のです。
ですので極座標による値によって計算をするとしても、
その結果は「ｘｙｚ直交座標系のｘ軸で測った値」を出しているわけです。

もう少し詳しく見ると、そのような場合には極座標変換を使用していますがベクトルとして考えている加速度ベクトルや力ベクトルは成分を「ｘ成分」「ｙ成分」「ｚ成分」として考えています。図的にはｘ軸、ｙ軸、ｚ軸に平行なベクトルの合計として１つの加速度ベクトルや力ベクトルを構成します。

では、加速度や力のベクトルを直交座標ではない成分表示で「ｒ成分」「θ成分」「φ成分」のように表して、図的にも「ある点での曲線の接線方向」を向いたベクトルの合計として１つの加速度ベクトルや力ベクトルを構成できるのか？
という事を考えると、結論を言うと「それは可能である」という事になるのです。

そのような場合の運動方程式は「力が質量と加速度に比例する」という関係は直交座標の時と同じですが、成分ごとに見るとある曲線の接線方向の加速度成分と力の成分を考える事になるわけです。

そのように考える時の具体的なベクトルの成分の変換方法を以下述べていきますが、
一般の曲線座標系への変換は話が複雑過ぎるので、物理学等で使われる事があって数学的にも比較的話が穏やかで済む直交曲線座標系への変換に限定して話を進めていきます。
（と言っても、それでも多少複雑になります。）

直交曲線座標とは、聞き慣れない事も多いかと思いますが
具体的には極座標や球面座標、円柱座標のようなものを指します。
これらの座標系では、座標軸に相当する「座標曲線」が任意の点で直交します。
通常のｘｙｚの直交座標系も、直交曲線座標系の特別な場合であるという見方もできます。

他方で、物理の法則を数式で表す時に座標系ごとに形を変換しないといけないというのでは一般論として議論する時に不便であるという考え方があります。
その考え方のもとで、変分原理による計算で導出する「座標系に依存しない運動方程式等の形」というものも存在します。（ラグランジュ型の運動方程式などとも呼ばれます。）
力学の分野である「解析力学」では、そのような考察を計算によって行います。

基本ベクトルと成分の直交曲線座標系への変換方法

ベクトルを含む微分方程式を座標系ごとの形に変換する時に、まず第一に重要となるのがベクトルを構成する基本ベクトルに対する成分の変換方法です。ここではその具体的な方法について説明します。

直交座標上のベクトルは、
（１，０，０）と（０，１，０）と（０，０，１）という
３つの基本ベクトルの線形結合で表す事ができます。
それらをそれぞれ\(\overrightarrow{e_x}\)，\(\overrightarrow{e_y}\)，\(\overrightarrow{e_z}\) と表す事にすると
任意のベクトルは実数a，ｂ，ｃを使って\(\overrightarrow{A}=a\overrightarrow{e_x}+b\overrightarrow{e_y}+c\overrightarrow{e_z}\)と書けます。
そして、ここで使った実数a，ｂ，ｃはそれぞれベクトルの成分であるわけです。
（数学の理論上はこれらの成分は複素数を使っても可です。）

曲線座標でも実は同じような考え方ができて、直交座標からの変換を考える時は基本ベクトルは「向きが座標曲線の勾配ベクトルである単位ベクトル」であり、ここで言う勾配ベクトルはｘ，ｙ，ｚで考えたものを指しています。
【■参考：ベクトル解析の概論の記事（勾配ベクトルの微分による定義など）】

より具体的には１つの座標曲線をｘｙｚ直交座標でu＝F(ｘ，ｙ，ｚ)で表せるとして grad u により表されますが、実際に直交曲線座標で考える時には「ｒ方向」「θ方向」「φ方向」といった形で図形的に把握していればよい事も多いと言えます。そこで、曲線座標における基本ベクトル \(\overrightarrow{e_r}\)，\(\overrightarrow{e_\theta}\)，\(\overrightarrow{e_{φ}}\) は分かっているものとして次に成分のほうを考えます。

直交座標系曲線座標系
$$\large{\overrightarrow{A}=A_x\overrightarrow{e_x}+A_y\overrightarrow{e_y}+A_z\overrightarrow{e_z}}$$$$\large{\overrightarrow{A}=A_r\overrightarrow{e_r}+A_{\theta}\overrightarrow{e_\theta}+A_{φ}\overrightarrow{e_φ}}$$

ここで、曲線座標系が直交曲線座標であるならば
ベクトルの成分の変換は局所的には方向余弦を使った線形結合の形で表す事ができます。

方向余弦とはその名の通り三角関数の cosθの形で表される量ですが、ここでは角度の値はあまり重要でないのでCの文字と添え字を使って表す事にします。
直交曲線座標系の３つの各基本ベクトルからの、直交座標系のｘ軸、y軸、ｚ軸への９つの方向余弦を次のようにここでは表記します。

ここでの方向余弦の
記号の表		ｘ軸に対してｙ軸に対してｚ軸に対する
ｒ曲線の基本ベクトル
\(\overrightarrow{e_r}\)から		CrｘCrｙCrｚ
θ曲線の基本ベクトル
\(\overrightarrow{e_\theta}\)から		CθｘCθｙCθｚ
φ曲線の基本ベクトル
\(\overrightarrow{e_{φ}}\)から		CφｘCφｙCφｚ

これらの方向余弦を使う事で、各点における基本ベクトルと個々のベクトルの成分を直交曲線座標系のものに変換できます。

方向余弦を使ったベクトル成分の変換公式

上記の９つの方向余弦と、ｘｙｚ直交座標系での成分を使う事で
直交曲線座標系でのベクトルの３つの成分は次のように表されます。 $$\large{A_r=C_{rx}A_x+C_{ry}A_y+C_{rz}A_z}$$ $$\large{A_{\theta} =C_{\theta x}A_x+C_{\theta y}A_y+C_{\theta z}A_z}$$ $$\large{A_φ=C_{φx}A_x+C_{φy}A_y+C_{φz}A_z}$$ この式は、元々は「原点を共有する２つの直交座標におけるベクトルの成分の変換公式」です。
ただし直交曲線座標では基本ベクトルとなる３つのベクトルが互いに直交するので、
各点での方向余弦を関数として表すという前提のもと、同じ変換公式を適用できます。

そこで次は、これらの方向余弦は具体的にどのような数式で表されるのかが問題になります。
それが分れば一般の変換公式を作れるわけです。

変換で使う「方向余弦」を微分により表す公式

方向余弦とは基本的には「余弦」なので「底辺／斜辺」の関係を使います。ただし基本ベクトルは座標曲線の接線ベクトルとして考えていますから方向余弦も微分や偏微分で考える必要があります。また、直交曲線座標系の基本ベクトルからｘｙｚ直交座標系の軸への方向余弦の表し方は実は２つあって、どちらを使っても同じ結果を得ます。

直交曲線座標系におけるｘｙｚ軸への方向余弦の２つの表現方法

座標曲線をu，ｖ，ｗとして、u＝u(ｘ，ｙ，ｚ)に対する
ｊ軸（ｘ，ｙ，ｚ軸のいずれか）の方向余弦は、 u の弧長をl(u)とした時に
次の２通りの表し方があります。
■勾配ベクトル（ｘｙｚ直交座標系で表したもの）を使う方法
勾配ベクトルは grad u＝（∂u／∂ｘ，∂u／∂ｙ，∂u／∂ｚ）で表されるベクトルであり
（ナブラ記号を使うと grad u＝∇u）、gradj uは勾配ベクトルのｊ成分で∂u／∂ｊの事です。
直交曲線座標系で成立する|gradu|＝ｄu／ｄｌの関係式も使っています（証明と説明は後述）。ｌはu曲線の弧長で、「u増加する向き」にｌが増える方向で考えます。（その時ｄu／ｄｌ≧０） $$ C_{uj}=\frac{\mathrm{grad}_ju}{|\mathrm{grad}u|}=\frac{dl}{du}\frac{\partial u }{\partial j} $$ ■弧長を斜辺とする方法
（u曲線上では、他の座標曲線の変数は一定でｄｖ／ｄｌ＝０およびｄｗ／ｄｌ＝０） $$ C_{uj}=\frac{dj}{dl}=\frac{\partial j}{\partial u}\frac{du}{dl}+\frac{\partial j}{\partial v}\frac{dv}{dl}+\frac{\partial j}{\partial w}\frac{dw}{dl}$$ $$ =\frac{\partial j}{\partial u}\frac{du}{dl}$$ 弧長に対するuによる微分での導関数ｄｌ／ｄuは次のように表されます。 $$\frac{dl}{du}=\sqrt{\left(\frac{\partial x}{\partial u}\right)^2+\left(\frac{\partial y}{\partial u}\right)^2+\left(\frac{\partial z}{\partial u}\right)^2}$$ また、ｄｌ／ｄuは１変数の導関数なのでｄu／ｄｌを次のように表せます。
（逆関数の微分公式によります。） $$\frac{du}{dl}=\frac{1}{\Large{\frac{dl}{du}}}=\frac{1}{\large{\sqrt{\left(\frac{\partial x}{\partial u}\right)^2+\left(\frac{\partial y}{\partial u}\right)^2+\left(\frac{\partial z}{\partial u}\right)^2}}}$$

極座標や球面座標への基本ベクトルおよび成分の変換を行う時には
具体的にはｘ＝ｒcosθなどと表す事から∂ｘ／∂θなどが計算しやすい場合が多くあります。その時には上記の「弧長を斜辺とする方法」を使ったほうが比較的分かりやすくなります。（この記事の後半でもそちらの形の公式を使用。）

ｄｌ／ｄθ や ｄθ／ｄｌを表す事になる弧長の式については、次に見て行くように球面座標であればｒ，θ，φの３つ分計算しておく必要があります。平面の極座標であればｒとθの２つ分です。

勾配を使った表す方は、直交曲線座標系で成立する |grad θ|＝ｄθ／ｄｌの関係を使ってさらに変形できます。ただし、
曲線の弧長を表す式の元の形

曲線の弧長については元々は定積分で次のように書く事ができて、
上記ではそれを微分した導関数を使用しています。$$l(u)=\int_0^u\sqrt{\left(\frac{\partial x}{\partial u}\right)^2+\left(\frac{\partial y}{\partial u}\right)^2+\left(\frac{\partial z}{\partial u}\right)^2}dt$$ 微分は、ここでの変数で言うとuで行います。 この式は曲線を折れ線に近似して図的に見る事でも理解可能ですが、解析学的に証明もできる式です。

同じ方向余弦の表し方が２つ存在する事と、
|grad u|＝ｄu／ｄｌの関係式についての証明と説明

勾配ベクトルについて一般的に成立するのは、スカラー場の値が一定値となっている「等位面」に対して必ず垂直であるというものです。（以下、等位面に含まれる曲線を「等位線」と呼んでおきます。）
極座標のθ曲線である「原点を中心とする同心円」の円周上では
半径が一定であり同心円は「ｒが一定値である等位線」を構成しています。
球面座標ではｒが一定値の球面が等位面として存在します。
スカラー関数F(ｘ，ｙ，ｚ)と弧長がｌで表される曲線があるとして、曲線上の座標を成分とするベクトルを\(\overrightarrow{r}=(x(l),y(l),z(l))\)とします。
曲線上でｄＦ／ｄｌを計算すると次式になります。（合成関数に対する偏微分の公式を使用。）$$\frac{dF}{dl}=\frac{\partial F}{\partial x}\frac{dx}{dl}+\frac{\partial F}{\partial y}\frac{dy}{dl}+\frac{\partial F}{\partial z}\frac{dz}{dl}=(\mathrm{grad}F)\cdot\frac{d\overrightarrow{r}}{dl}$$ $$ここでもし\frac{dF}{dl}=0であるなら、(\mathrm{grad}F)\cdot\frac{d\overrightarrow{r}}{dl}=0$$ つまり「Fの値が変化しない曲線」＝「Fの等位線」においては
「Fの勾配ベクトルは曲線の接線ベクトルに常に垂直」という事になります。
ところで、直交曲線座標においては１つの座標曲線上では他の変数の値が一定であり、ｒ曲線とφ曲線上でθは一定値です。
また、θ曲線上の任意の点ではｒ曲線およびφ曲線との交点が存在します。
【より詳しく言えばこれらの曲線は「曲面」を構成しています。】
ところで直交曲線座標系であればｒ曲線およびφ曲線はθ曲線との交点で直交します。
これは具体的には任意の点での「曲線の接線ベクトル」同士が直交するという意味です。
先ほどの考察から、勾配ベクトル gradθ は
「θが一定値であるφ曲線およびθ曲線上の任意の点」での接線ベクトルに直交します。
よって、gradθ はu曲線上の任意の点において、その点でu曲線と交わるφ曲線およびθ曲線に直交しています。
そして、u曲線自体もφ曲線およびθ曲線に直交しているのでした。 という事はその点においてu曲線の接線ベクトルとgradθは平行なベクトルである事になり、それはすなわちgradθがその点におけるθ曲線の接するベクトルの１つである事を示しています。
先ほどのｄＦ／ｄｌの式においてFの代わりにθを考えると $$\frac{d\theta}{dl}=\frac{\partial \theta}{\partial x}\frac{dx}{dl}+\frac{\partial \theta}{\partial y}\frac{dy}{dl}+\frac{\partial \theta}{\partial z}\frac{dz}{dl}=(\mathrm{grad}\theta)\cdot\left(\frac{dx}{dl},\hspace{2pt}\frac{dy}{dl},\hspace{2pt}\frac{dz}{dl}\right)$$ と表せるわけですが
ｄｘ／ｄｌ等は、大きさがΔｌであるベクトル（Δｘ，Δｙ，Δｚ）における
方向余弦 であるΔｘ／ΔｌのΔｌ→０の極限値でもあります。
すると、方向余弦についての関係式により、
θ曲線の接線ベクトル（ｄｘ／ｄｌ，ｄｙ／ｄｌ．ｄｚ／ｄｌ）方向の
gradθの成分はｄθ／ｄｌである事になります。
よって、何らかの余弦cosω（）を使って|gradθ|cosω＝ｄθ／ｄｌと表せる事になりますが、
θ曲線の接線ベクトルと gradθは同じ点でθ曲線に接するのでcosωの値は１か－１です。
上式でF＝u(ｘ，ｙ，ｚ)で表す場合【より正確にはこれは曲面を表します】には、弧長であるｌは「u増加する向きにｌが増えて行く方向」で考えます。
そのためｄu／ｄｌ ≧０であるので、
cosω＝１であり（－１ではなく、という意味）|gradθ|＝ｄθ／ｄｌ
するとgradθとθ曲線の接線ベクトルは同じ向きのベクトルであるのでｘ軸，y軸，ｚ軸への方向余弦は「直角三角形の底辺／斜辺」＝「直交座標系でのベクトルの成分／ベクトルの大きさ」として同じ値を持ちます。
（向きは同じでも、ベクトルの大きさは異なります。|gradθ|＝ｄθ／ｄｌですがこれは接線ベクトルの大きさとは一般的に異なります。）
以上の事は直交曲線座標系の任意のu曲線で成立します。

補足として、ベクトルの「方向余弦」自体は余弦 cosθ であるので、軸に対する向きが同じであれば大きさはどのようなベクトルであっても底辺／斜辺の関係で方向余弦を表す事ができます。
つまり数学的には１つの方向余弦の表し方は無限にあるわけですが、ここでの一般的な変換に使えるような微分による方向余弦の表し方の方法としては上記の２通りがあるという事になります。

変換の具体例１（平面の極座標変換の場合）

ベクトルの基本ベクトルと成分に対して具体的に平面での極座標変換をしてみます。平面なので必要な方向余弦は４つで、それを表すために偏微分が４つと弧長の式が２つ必要になります。

まず、ｘとｙに対するｒとθの偏微分です。

極座標変換の時∂／∂ｒ∂／∂θ
ｘ＝ｒcosθcosθ－ｒsinθ
ｙ＝ｒsinθsinθ　ｒcosθ

次に弧長の計算です。∂ｘ／∂ｒなどを計算してあるので、公式に代入します。
ｄｒ／ｄｌなどを使う事になりますが、まずはｄｌ／ｄｒの形で記しておきます。

$$\frac{dl}{dr}=\sqrt{(\cos\theta)^2+(\sin\theta)^2}=1$$

$$\frac{dl}{d\theta}=\sqrt{(-r\sin\theta)^2+(-\cos\theta)^2}=\sqrt{r^2}=r$$

このように意外と簡単な式になります。
さらに、θのほうの弧長の式で出てきたｒは∂ｘ／∂θの式にあるｒと打ち消して方向余弦の値には含まれなくなります。（そのように計算が簡単になる事は一般的に保証されるわけではありませんが、球面座標の場合でも同じ事が起こります。）

方向余弦はCｒｘ＝(∂ｘ／∂ｒ)・(ｄｒ／ｄｌ)＝cosθ　のように計算します。
θについては例えばCθｘ＝(∂ｘ／∂θ)・(ｄｒ／ｄｌ)＝(－ｒsinθ)・(１／ｒ)＝－sinθです。
先ほど述べたようにｒは打ち消して式から無くなるわけです。

４つの方向余弦は具体的には次のような形になります。

  • Crｘ＝(∂ｘ／∂ｒ)・(ｄｒ／ｄｌ)＝cosθ
  • Crｙ＝(∂ｘ／∂ｒ)・(ｄｒ／ｄｌ)＝sinθ
  • Cθｘ＝(∂ｘ／∂ｒ)・(ｄｒ／ｄｌ)＝－sinθ
  • Cθｙ＝(∂ｘ／∂ｒ)・(ｄｒ／ｄｌ)＝cosθ

よってｒθ極座標系での基本ベクトルでの\(\overrightarrow{A}\)の成分は
Ａｒ＝CｒｘAｘ＋CｒｙＡｙ＝Aｘcosθ－Ａｙsinθ
Ａθ＝CθｘAｘ＋CθｙＡｙ＝Aｘsinθ＋Ａｙcosθ であり、
\(\overrightarrow{A}\)＝（Aｘcosθ－ＡｙsinθＡθ ，Aｘsinθ＋Ａｙcosθ）となります。

ところでこれらについて運動方程式等に適用するために微分を考える場合などはどうなるのか？という事については後述します。時間微分に関しては得られた変換の結果の式をそのままｔで微分すればよいのですが、元の座標系の値であるAｘに関する処理が必要となります。

極座標による基本ベクトルと成分の変換公式

ｘｙ直交座標系からｒθ極座標系に基本ベクトルと成分を変換する式は次のようになります。 $$A_r=\hspace{7pt}A_x\cos\theta+A_y\sin\theta$$ $$A_{\theta}=-A_x\sin\theta+A_y\cos\theta$$ 平面極座標への変換の場合には、直交座標を原点回りに回転させる形で
各点での局所的な変換を行うものとして図から導出する事もできます。

変換の具体例２（球面座標変換の場合）

次に球面座標の場合を見てみます。角度のとりかたはθとφの２箇所がありますが、ここでは平面極座標との関連を見やすくするためにθをｘｙ平面での角度にとり、Φをｒ曲線（と言っても直線ですが）とｚ軸のなす角にとって考えます。

９つの偏微分と３つの弧長をまとめると次の通りです。

球面座標変換の時∂／∂ｒ∂／∂θ∂／∂φ
ｘ＝ｒsinφcosθsinφcosθ－ｒsinφsinθｒcosφcosθ
ｙ＝ｒsinφsinθsinφsinθｒsinφcosθｒcosφsinθ
ｚ＝ｒcosφcosφ０－ｒsinφ
弧長式逆数（ｄｒ／ｄｌなど）
ｄｌ／ｄｒ１１
ｄｌ／ｄθｒsinφ１／(ｒsinφ)
ｄｌ／ｄΦｒ１／ｒ

弧長の式に関する具体的な計算は次のようになります。 $$\frac{dl}{dr}=\sqrt{\left(\frac{\partial x}{\partial r}\right)^2+\left(\frac{\partial y}{\partial r}\right)^2+\left(\frac{\partial z}{\partial r}\right)^2}=\sqrt{(\sin φ\cos\theta)^2+(\sinφ\sin\theta)^2+(\cos φ)^2}$$ $$=\sqrt{\sin^2φ(\cos^2\theta+\sin^2\theta)+\cos^2φ}=\sqrt{\sin^2φ+\cos^2φ}=1\hspace{60pt}$$ $$\frac{dl}{d\theta}=\sqrt{\left(\frac{\partial x}{\partial \theta}\right)^2+\left(\frac{\partial y}{\partial \theta}\right)^2+\left(\frac{\partial z}{\partial \theta}\right)^2} =\sqrt{(r\sin φ\sin\theta)^2+(r\sinφ\cos\theta)^2+0^2}\hspace{15pt}$$ $$=\sqrt{r^2\sin^2φ(\sin^2\theta+\cos^2\theta)}=\sqrt{r^2\sin^2φ}=r\sin φ\hspace{105pt}$$ $$\frac{dl}{dφ}=\sqrt{\left(\frac{\partial x}{\partial φ}\right)^2+\left(\frac{\partial y}{\partial φ}\right)^2+\left(\frac{\partial z}{\partial φ}\right)^2}\hspace{200pt}$$ $$ =\sqrt{(r\cos φ\cos\theta)^2+(r\cosφ\sin\theta)^2+(r\sin φ)^2}\hspace{115pt}$$ $$=\sqrt{r^2\cos^2φ(\cos^2\theta+\sin^2\theta)+r^2\sin^2 φ}=\sqrt{r^2(\cos^2φ+\sin^2φ)}=\sqrt{r^2}=r\hspace{0pt}$$ ｄｌ／ｄθの計算では、角度φは正弦sinφが０以上の値をとる範囲で考えるとします。それは０≦φ≦πの範囲になりますが、図的に見てもその範囲だけで考えても十分である事になります。それは球面座標においてはθの変化もあるからです。

以下、上記の結果と公式を適用して計算をしていく事で
基本ベクトルを直交座標から球面座標に変換した時のベクトルの変換の公式を得ます。

$$
方向余弦の式\hspace{5pt}C_{uj}=\frac{\partial j}{\partial u}\frac{du}{dl}\hspace{5pt}【u=r,\theta,φ\hspace{3pt}j=x,y,z】$$ $$（具体例）C_{\theta y}=\frac{\partial y}{\partial \theta}\frac{d\theta}{dl}=(r\sinφ\cos\theta)\cdot\frac{1}{r\sinφ}=r\cos\theta$$

方向余弦ｘ軸ｙ軸ｚ軸
r 曲線Cｒｘ＝sinφcosθCｒｙ＝sinφsinθCｒｚ＝cosφ
θ 曲線Cθｘ＝－sinθCθｙ＝cosθCθｚ＝0
φ 曲線Cφｘ＝cosφcosθCφｙ＝cosφsinθCφｚ＝－sinφ
球面座標による基本ベクトルと成分の変換公式
r 成分　Aｒ＝CrｘAx＋CrｙAy＋CrｚAz＝　Axsinφcosθ＋Aysinφsinθ＋Azcosφ
θ 成分　Aθ＝CθｘAx＋CθｙAy＋CθｚAz＝－Axsinθ＋Aycosθ
φ 成分　Aφ＝CφｘAx＋CφｙAy＋CφｚAz＝　Axcosφcosθ＋Aycosφsinθ－Azsinφ
θはｘｙ平面での角度、φはｚ軸とｒ曲線のなす角です。

φ＝π／２の時、すなわちｒ曲線が常にｘｙ平面にある時には
sinφ＝１および cosφ＝０を代入し、
さらにもとの直交座標でｚ成分Aｚ＝０とすれば平面極座標の時の変換公式になります。
（θ成分への変換式はφもAｚも含んでおらず、実は極座標の時と同じ式です。）

これらの式は
「ｘｙ平面での角度をΦとしてz軸とｒ曲線のなす角をθとした場合」には、
θとφを入れ換える事になります。

「ｘｙ平面での角度をΦ、z軸とｒ曲線のなす角をθとした場合」の変換公式
r 成分　Aｒ＝ CrｘAx＋CrｙAy＋CrｚAz ＝　Axsinθcosφ ＋Aysinθsinφ ＋Azcosθ
φ 成分　Aφ＝ CφｘAx＋CφｙAy＋CφｚAz ＝－Axsinφ＋Aycosφ
θ 成分 　Aθ＝CθｘAx＋CθｙAy＋CθｚAz ＝　Axcosθcosφ＋Aycosθsinφ－Azsinθ

これらの式は単なるθとφの文字の置き換えをしただけであり、
何か新しい変換を行ったという事ではありません。

球面座標の特別な場合として平面の極座標を考える時に、運動方程式におけるような場合では
図のφ＝π／２と合わせて「ベクトルのφ成分の時間微分が０である」という条件も考えると一般論としての球面座標から移行を考える事ができます。

運動方程式の球面座標系での成分表示の導出

各成分に対する時間微分を考える時には、直交座標での「ベクトルの時間微分」を１つのベクトルと考えて上記の変換公式を適用します。考え方は、１階の微分でも２階の微分でも同じになります。

  1. 直交座標の成分に対する時間微分ｄＡｘ／ｄｔなどを計算します。
    （２階微分をする時はｄ２Ａｘ／ｄｔ２を計算します。）
    ただし、計算結果は変換後の変数であるｒやθで表す必要があります。
  2. ベクトルの時間微分(ｄ／ｄｔ)\(\overrightarrow{A}\) は１つのベクトルであるので、変換の公式を適用して基本ベクトルの変換を行います。
  3. 変換の式に含まれる「直交座標で考えた時の成分」に、直交座標で考えた時間微分ｄＡｘ／ｄｔなどを代入します。

一番簡単な例（と言っても多少複雑ですが）で、
尚且つ重要なベクトルは物体の位置を表す\(\overrightarrow{r}\)＝（ｘ，ｙ，ｚ）です。
何の断り書きもなければ直交座標の成分で表されています。

次に、\(\overrightarrow{r}\)＝（ｘ，ｙ，ｚ）に対する
１階の時間微分を表す速度ベクトル\({\overrightarrow{v}=\Large\frac{d\overrightarrow{r}}{dt}}\)＝(ｖｘ，ｖｙ，ｖｚ)と、
２階の時間微分である加速度ベクトル\(\overrightarrow{a}=\Large{\frac{d^2\overrightarrow{r}}{dt^2}}\)＝(aｘ，aｙ，aｚ)について
基本ベクトルを球面座標系に変化した場合の成分はどうなるかを見てみます。
（その特別な場合として平面極座標への変換も分かります。）

ｖｘ＝ｄｘ／ｄｔ，ｖｙ＝ｄｙ／ｄｔ，ｖｚ＝ｄｚ／ｄｔおよび
aｘ＝ｄ２ｘ／ｄｔ２，aｙ＝ｄ２ｙ／ｄｔ２，aｚ＝ｄ２ｚ／ｄｔ２
ｒ，θ，φの時間微分については２階微分のほうの式が少し複雑なので「ドット」で表すのがここでは便利です。ドットが２つ付いていたら２階での時間微分を意味します。
ｄｒ／ｄｔ＝\(\dot{r}\)， ｄθ／ｄｔ＝\(\dot{\theta}\)， ｄφ／ｄｔ＝\(\dot{\varphi}\)
ｄ２ｒ／ｄｔ２＝\(\ddot{r}\)， ｄ２θ／ｄｔ２＝\(\ddot{\theta}\)， ｄ２φ／ｄｔ２＝\(\ddot{\varphi}\)
の表記で式を整理します。

ｘとｙについては積の微分公式を２回使う形で計算をします。
また、θやφをｔの関数として考えているので
合成関数の微分公式も同時に使っていく事になります。
例えば sinθやcosφなどの項の時間微分は
(ｄ／ｄｔ)sinθ＝(ｄθ／ｄｔ)cosθ=\(\dot{\theta}\cos\theta\)
(ｄ／ｄｔ)cosφ＝－(ｄφ／ｄｔ)sinφ=\(-\dot{\varphi}\sin\varphi\) のようになります。

等速円運動の時のようにｘ＝Rcos(ωｔ)などとする例ではｒ＝Ｒは定数であり、θ＝ωｔの時間微分だけを考えれば良い事になります。（また、平面運動なのでφは式に含まれません。）
しかしここではｒ，θ，φがいずれもｔの関数であるとして一般的な式の形を書きます。

\(\overrightarrow{r}\)＝（ｘ，ｙ，ｚ）ｄ／ｄｔ
ｘ＝ｒsinφcosθ\(\dot{r}\sin\varphi\cos\theta+\dot{\varphi}r\cos\varphi\cos\theta-\dot{\theta}r\sin\varphi\sin\theta\)
ｙ＝ｒsinφsinθ\(\dot{r}\sin\varphi\sin\theta+\dot{\varphi}r\cos\varphi\sin\theta+\dot{\theta}r\sin\varphi\cos\theta\)
ｚ＝ｒcosφ\(\dot{r}\cos\varphi-\dot{\varphi}r\sin\varphi\)

次に、理論的には１階微分をさらに時間微分する形で２階微分を計算して変換の公式に当てはめれば良い事になりますが、その直接計算は実はかなり面倒です。

具体的な計算式は補足・参考用の資料として記事の最後に載せるとして、計算結果の式は次のようになります。

基本ベクトルを球面座標系に変更した時の加速度ベクトル

２階の時間微分を計算後、
加速度ベクトルに変更の公式を適用するとｒ，θ，φ成分は次のようになります。 $$a_r=\ddot{r}-\dot{\varphi}^2r-\dot{\theta}^2r\sin^2\varphi$$ $$a_{\theta}=2\dot{r}\dot{\theta}\sin\varphi+2r\dot{\varphi}\dot{\theta}\cos\varphi+r\ddot{\theta}\sin\varphi$$ $$a_{\varphi}=2\dot{r}\dot{\varphi}+r\ddot{\varphi}-r\dot{\theta}^2\sin\varphi\cos\varphi$$ また、θ成分に関しては次のようにも書けます。 $$a_{\theta}=\frac{1}{r\sin\varphi}\frac{d}{dt}\left(r^2\dot{\theta}\sin^2\varphi\right)$$ ここではｘｙ平面の角度をθとしているので、
もしその角度をφとおくなら上式はθとφの文字を入れ替えた形になります。

上式でφ＝π／２とおき、時間によるφの変化はないなら平面の極座標での変換を表します。
φ成分がなくなり、ｒ成分とθ成分の式中でsinφ＝１となるので式は比較的簡単になります。

平面の極座標の場合

球面座標系への加速度ベクトルの変換の式においてφ＝π／２かつｄφ／ｄｔ＝０であれば
平面における極座標での加速度ベクトルの変換の式になります。 $$a_r=\ddot{r}-\dot{\theta}^2r$$ $$a_{\theta}=2\dot{r}\dot{\theta}+r\ddot{\theta}=\frac{1}{r}\frac{d}{dt}\left(r^2\dot{\theta}\right)$$ ここではｘｙ平面の角度をθとしているので、
もしその角度をφとおくなら上式はθとφの文字を入れ替えた形になります。

これらの結果から、球面座標系での運動方程式を作る事ができます。

運動方程式は「力ベクトル＝加速度ベクトルと質量の積」という形です。そこで、成分に分けた時に加速度ベクトルの成分として上記の式を使えばよいわけです。それらの成分とはｘ成分やｙ成分ではなく、ｒ成分やθ成分であるわけです。

球面座標系における運動方程式の成分表示

球面座標系で運動方程式はｒ成分、θ成分、φ成分ごとに次のように表されます。 加速度ベクトルに変更の公式を適用するとｒ，θ，φ成分は次のようになります。 $$F_r=m\left(\ddot{r}-\dot{\varphi}^2r-\dot{\theta}^2r\sin^2\varphi\right)\hspace{5pt}(=ma_r)$$ $$F_{\theta}=m\left(2\dot{r}\dot{\theta}\sin\varphi+2r\dot{\varphi}\dot{\theta}\cos\varphi+r\ddot{\theta}\sin\varphi\right)\hspace{5pt}(=ma_\theta)$$ $$F_{\varphi}=m\left(a_{\varphi}=2\dot{r}\dot{\varphi}+r\ddot{\varphi}-r\dot{\theta}^2\sin\varphi\cos\varphi\right)\hspace{5pt}(=ma_\theta)$$ 平面の極座標においては次のようになります。 $$F_r=m\left(\ddot{r}-\dot{\theta}^2r\right)$$ $$F_{\theta}=m\left(2\dot{r}\dot{\theta}+r\ddot{\theta}\right)=\frac{m}{r}\frac{d}{dt}\left(r^2\dot{\theta}\right)$$ このように運動方程式を書く時には、
力ベクトルの成分も加速度ベクトル同様にｒ成分、θ成分、φ成分として表されます。
「力」は任意の方向にベクトルと同じ規則で分解できるので（実験で示されます）、
自由な方向での成分を考える事ができます。

これを見ると、一応そのように表せるといっても結構複雑です。直交曲線座標の中では比較的構造が単純で分かりやすい球面座標系であっても、加速度ベクトルや運動方程式をその座標系で考えるとなると直交座標系からの基本ベクトルと成分の変換はそれほど容易でない事が分かります。

平面上の極座標で見れば比較的形は簡単にはなりますが、直交座標での形と比べるとやはり複雑さは増しています。運動方程式の極座標系での成分表示は、回転を伴う運動の一部の解析では有効に機能します（例えば万有引力だけが働く物体の軌道を調べる時など）。

参考：球面座標に変換後の加速度ベクトルの成分計算

参考資料として、非常に地味ですが
速度ベクトルの加速度ベクトルの各成分を直接計算した場合の式を記します。

ここでの計算では、積の微分の規則から式全体は \(\ddot{r}\)の項や\(\dot{r}\dot{\theta}\)の項に分けて、変換の公式を適用までした値を１つずつ計算して最後に合計値を出します。それら自体は単なる微分と三角関数の計算問題なので、「確かに結果の式が直接計算でも得られる」という事を見るための参考用資料です。

（再掲）球面座標における基本ベクトルと成分の変換
r 成分　Aｒ＝CrｘAx＋CrｙAy＋CrｚAz＝　Axsinφcosθ＋Aysinφsinθ＋Azcosφ
θ 成分　Aθ＝CθｘAx＋CθｙAy＋CθｚAz＝－Axsinθ＋Aycosθ
φ 成分　Aφ＝CφｘAx＋CφｙAy＋CφｚAz＝　Axcosφcosθ＋Aycosφsinθ－Azsinφ
θはｘｙ平面での角度、φはｚ軸とｒ曲線のなす角
\(\overrightarrow{r}\)＝（ｘ，ｙ，ｚ）ｄ／ｄｔ（１階微分）
ｘ＝ｒsinφcosθ\(\dot{r}\sin\varphi\cos\theta+\dot{\varphi}r\cos\varphi\cos\theta-\dot{\theta}r\sin\varphi\sin\theta\)
ｙ＝ｒsinφsinθ\(\dot{r}\sin\varphi\sin\theta+\dot{\varphi}r\cos\varphi\sin\theta+\dot{\theta}r\sin\varphi\cos\theta\)
ｚ＝ｒcosφ\(\dot{r}\cos\varphi-\dot{\varphi}r\sin\varphi\)

具体的なｒ，θ，φ成分の計算

ｔによる２階導関数（２階微分）はｒ，θ，φ成分のいずれにも共通して使えます。
異なるのは変換公式における方向余弦になります。
この表は、例えば式中の\(\ddot{r}\)の項の係数は
２階微分を行った時点の変換前でｘにおいては\(\ddot{r}\)sinφcosθであり、
ｒ成分への変換用の方向余弦sinφcosθを乗じるとsin２φcos２θとなっている事を記しています。
ｙとｚについても同様に計算し、例として\(\ddot{r}\)の項については合計すると係数の値は１になります。

sin２θ＋cos２θ＝１の関係などで三角関数の大部分は式から消えて、
プラスマイナスで打ち消して無くなる項も多くあるために
最終的な結果で残る項は比較的少なくなります。

\(\ddot{r}\)変換前ｒ成分θ成分φ成分
ｘ由来sinφcosθsin２φcos２θ－sinφsinθcosθsinφcosφcos２θ
ｙ由来sinφsinθsin２φsin２θsinφsinθcosθsinφcosφsin２θ
ｚ由来cosφcos２φ０－sinφcosφ
合計・・・１００
\(\dot{r}\dot{\theta}\)係数ｒ成分θ成分φ成分
ｘ由来－2sinφsinθ－2sin２φsinθcosθ－2sinφsin２θ－2sinφcosφ
sinθcosθ
ｙ由来2sinφcosθ2sin２φsinθcosθ2sinφcos２θ2sinφcosφ
sinθcosθ
ｚ由来なしなしなしなし
合計・・・０２sinφ０
\(\dot{r}\dot{\varphi}\)変換前ｒ成分θ成分φ成分
ｘ由来２cosφcosθ２cosφsinφcos２θ－２cosφcosθsinθ２cos２φcos２θ
ｙ由来２cosφsinθ２cosφsinφsin２θ２cosφcosθsinθ２cos２φsin２θ
ｚ由来－２sinφ－２cosφsinφ０２sin２φ
合計・・・００２
\(\ddot{\varphi}\)変換前ｒ成分θ成分φ成分
ｘ由来ｒcosφcosθｒsinφcosφcos２θ－ｒcosφcosθsinθｒcos２φcos２θ
ｙ由来ｒcosφsinθｒsinφcosφsin２θｒcosφcosθsinθｒcos２φsin２θ
ｚ由来－ｒsinφ－ｒsinφcosφ０ｒsin２φ
合計・・・００ｒ
\(\dot{\varphi}^2\)変換前ｒ成分θ成分φ成分
ｘ由来－ｒsinφcosθ－ｒsin２φcos２θｒsinφcosθsinθ－ｒcosφsinφcos２θ
ｙ由来－ｒsinφsinθ－sin２φsin２θ－ｒsinφcosθsinθ－ｒcosφsinφsin２θ
ｚ由来ｒcosφ－ｒcos２φ０ｒcosφsinφ
合計・・・－ｒ００
\(\ddot{\theta}\)変換前ｒ成分θ成分φ成分
ｘ由来－ｒsinφsinθ－ｒsin２φcosθsinφｒsinφsin２θ－ｒcosφsinφ
cosθsinθ
ｙ由来ｒsinφcosθｒsin２φcosθsinφｒsinφcos２θｒcosφsinφ
cosθsinθ
ｚ由来なしなしなしなし
合計・・・０ｒsinφ０
\(\dot{\theta}^2\)変換前ｒ成分θ成分φ成分
ｘ由来－ｒsinφcosθ－ｒsin２φcos２θｒsinφcosθsinθ－ｒcosφsinφ
cos２θ
ｙ由来－ｒsinφsinθ－ｒsin２φsin２θ－ｒsinφcosθsinθ－ｒcosφsinφ
sin２θ
ｚ由来なしなしなしなし
合計・・・－ｒsin２φ０－ｒcosφsinφ
\(\dot{\theta}\dot{\varphi}\)変換前ｒ成分θ成分φ成分
ｘ由来－2ｒcosφsinθ－2cosφsinφcosθsinθ2ｒcosφsin２θ－2ｒcos２φ
cosθsinθ
ｙ由来2ｒcosφcosθ2cosφsinφosθsinθ2ｒcosφcos２θ2ｒcos２φ
cosθsinθ
ｚ由来なしなしなしなし
合計・・・０2ｒcosφ０

成分ごとに合計すると、加速度ベクトルの変換後の各成分は
\(a_r＝\dot{r}-\dot{\varphi}^2r-\ddot{\theta}^2r\sin^2\varphi\)
\(a_{\theta}＝2\dot{r}\dot{\theta}\sin\varphi+2\dot{\theta}\dot{\varphi}r\cos\varphi+\ddot{\theta}r\sin\varphi\)
\(a_{\varphi}＝2\dot{r}\dot{\varphi}+\ddot{\varphi}r-\dot{\theta}^2r\cos\varphi\)
になります。

他の計算の仕方としては、変換の公式を先に使って例えばｖｒ＝ｖxsinφcosθ＋ｖysinφsinθ＋ｖzcosφの形で表して、その式の時間微分をするという方法もあります。その場合でも計算式は多少長くなります。

方向余弦の定義と公式

恭平

方向余弦（direction cosine）とはベクトルに対して考えられる補助的な量で、ベクトルの大きさに乗じる事で各成分の値になるような余弦（コーサイン、cos）を指します。（空間ベクトルの平面への射影を考える時の余弦とは一般的に異なるものです。）

この方向余弦の応用として特に重要であるの直交座標同士の座標変換です。
（局所的には直交座標から直交曲線座標への変換もできます。）

■関連記事：ベクトルの内積

■応用例：直交曲線座標系の成分にベクトルを変換する方法

「方向余弦」の定義

方向余弦とは、ベクトルと座標軸とのなす角に対して考える余弦であり、ｘｙｚの空間での直交座標なら１つのベクトルに対して３つ定義されます。平面であれば２つです。

方向余弦の定義

大きさが０でないベクトル\(\overrightarrow{A}\) ＝（A１，A２，A３）に対して
\(\left|\overrightarrow{A}\right|=A\) （ ＞０）とおくとして、
\(A\cos\theta_x=A_1\),　 \(A\cos\theta_y=A_2\),　 \(A\cos\theta_z=A_3\) である時、
余弦 cosθｘ，cosθｙ，cosθｚ を特に「方向余弦」と呼ぶことがあります。
本質的に関数としては普通の余弦 cosθと同じものではありますが、
ベクトルに関する性質と組み合わせる事で特有の関係式がいくつか成立するものになります。

「おおきさが０でないベクトル」という条件を付しているのは、ゼロベクトルに対して方向余弦の定義を適用するとベクトルの大きさも０ですが、成分も全て０なので方向余弦は「任意の角度の余弦」であってもよい事になってしまうからです。
そのため、定義自体をできないわけではありませんがゼロベクトルに対する方向余弦は
「あまり意味のないもの」になってしまうので、ここでは除外して考えるという事です。

方向余弦をベクトルの大きさに乗じる事で、ベクトルの成分が計算されます。
具体的で簡単な数値で考えてみると、例えば（１，１，１）のようなベクトルなら
ベクトルの大きさは\(\sqrt{3}\)なので、各軸に対する方向余弦は３つとも等しく１／\(\sqrt{3}\)になります。
\(\sqrt{3}\cdot\frac{1}{\large{\sqrt{3}}}=1\)であり、大きさ×方向余弦＝成分となっています。

この時に、具体的な角度の値は必ずしも分かっていなくてもよい事も多くあります。
cosθ＝１／\(\sqrt{3}\)に対しては角度は約５４．７°、弧度法で0.955≒0.3πとも書けますが、
角度の値よりも「余弦の値」のほうが重要である場合も少なからずあります。
（特にこの記事で見て行く方向余弦の公式や諸性質・応用ではその傾向があります。）

このように方向余弦の定義自体は比較的簡単なものですが、
注意すべき点があるとすれば方向余弦は３次元の空間の場合には一般的に
「ベクトルをｘｙ平面やｘｚ平面に射影する余弦とは異なる」という事です。
平面であれば、方向余弦はｘ軸あるいはy軸に対してベクトルを射影する余弦でもあります。
空間の場合でも確かに「軸に対する射影」を行うベクトルであるとは言えますが、それはｘｙ平面等の「平面に対する射影」とは異なるのです。

図で見ると、一般的に３次元空間でのベクトルの方向余弦はｘｙ平面等に対して「斜めになった平面」における直角三角形の１つの角に対する余弦となります。

公式１：方向余弦の２乗和に対する公式

方向余弦は普通の余弦と同じく三角比や三角関数の公式が使えますが、特に方向余弦に対して成立する公式として「３つの方向余弦（平面であれば２つ）の２乗の和は１になる」というものがあります。

方向余弦の２乗和に対して成立する公式

３次元空間における３つの方向余弦に対しては次式が成立します。 $$\large{\cos^2\theta_x+\cos^2\theta_y+\cos^2\theta_z=1}$$ 平面では次式です。
（空間で１つの方向余弦だけが０と考えても同じ。） $$\large{\cos^2\theta_x+\cos^2\theta_y=1}$$ この公式は「方向余弦」について成立するものであり、
一般の余弦 cosθで成り立つものではありません。
平面の場合では図を見ると実質的には sin２θ＋cos２θ＝１ と同じである事も分かるでしょう。

この公式は式で考えても導出できますし、図による平面幾何的な導出も可能です。
（式で考えたほうが、実はやや簡単かもしれません。）

証明

式で見る場合には、ベクトルの大きさ（の２乗）を成分で敢えて表してみると公式がすぐに出ます。（同じベクトルでの内積で考えても同じです。）

ベクトルの大きさをAとすると方向余弦を使った成分は
（A cosθｘ，A cosθｙ，A cosθｚ）です。ここでA＞０であるとします。
成分を使って敢えて大きさの２乗を計算すると
A２ cos２θｘ＋A２ cos２θｙ＋A２ cos２θｚです。
しかし考えているベクトルの大きさは A なのですから、その式の値はA２です。
A２ cos２θｘ＋A２ cos２θｙ＋A２ cos２θｚ＝A２
A＞０なので
cos２θｘ＋cos２θｙ＋ cos２θｚ＝１となり、公式が導出されます。

図で見る場合は、平面だと分かりやすくて式で見る場合と同じように三平方の定理で斜辺の長さを見れば数式だけで考えた時と同じ式を得ます。

また、同じ角度で三角比の意味での余弦を２回考えるという方法も可能です。
すなわち長さ A の斜辺に対して A cosθ を考えて、さらにそこを斜辺とする線分を探します。
するとベクトルが作る直角三角形において直角の頂点から斜辺に垂線を下ろした時に、
そこを境にA cos２θｘの長さの部分とA cos２θｙの長さに分かれる部分となる事が分かります。

空間の場合も似た考察ができますが、平面と比べるとどうしても単純さが失われる傾向があります。

三平方の定理を使うのが一番早く、式で考える場合と結局同じになります。
それ以外の方法だと、かえって複雑です。
図形的にはベクトルの辺はA cos２θｘ＋A cos２θｙの部分とA cos２θｚの部分に分かれます。

いずれにしても、方向余弦に関しての性質を調べる時には平面の場合は図形的な考察は比較的容易でも、空間の場合では式で取り扱ったほうが見やすい事を示唆しています。

平面の場合は、２つの方向余弦のうち１つはもう片方の角度から見た正弦と実質的には同じです。
平面の場合は図で見ても比較的分かりやすいですが、空間の場合だとやや複雑になる傾向があります。後述していく方向余弦の関係式や公式の証明では基本的に内積などの式による計算を使っています。

公式２：ベクトルの直線に対する射影についての関係式

ベクトル\(\overrightarrow{A}\) ＝（A１，A２，A３）と始点のみを共有する直線があるとして、
始点からの長さが「その直線への\(\overrightarrow{A}\)の射影に等しい」ベクトルを\(\overrightarrow{B}\) とします。
どちらのベクトルもゼロベクトルではないとします。
その他、次のように設定を考えます。

  • \(\overrightarrow{B}\) ＝（B１，B２，B３）とします。
  • \(\overrightarrow{A}\)と\(\overrightarrow{B}\) とのなす角をφとします。
  • \(\overrightarrow{A}\)の方向余弦の角度をθｘ，θｙ，θｚとします。
  • \(\overrightarrow{B}\)の方向余弦の角度をωｘ，ωｙ，ωｚとします。
  • ベクトルの大きさについては\(\left|\overrightarrow{A}\right|=A\)（ ＞０）および \(\left|\overrightarrow{B}\right|=B\)（ ＞０） とおきます。

この時、B＝A cosφ ですが、他にも次の公式が成立します。

ベクトルの直線への射影と方向余弦の関係式

上記の設定のもとで、次式が成立します。 $$\large{\cosφ=\cos\theta_x\cos\omega_x+\cos\theta_y\cos\omega_y+\cos\theta_z\cos\omega_z}$$ $$\large{B=A_x\cos\omega_x+A_y\cos\omega_y+A_z\cos\omega_z}$$ これらの式が一体何を言っているのかというと、
最初の式は２つのベクトルのなす角の余弦を互いの方向余弦の積の和で表せる事、
２式目は１つのベクトルの大きさを３つの方向余弦と
「射影のもとになっている別のベクトルの成分」で表せるという事です。
また、１式目は２式目を導出するのに使う式でもあります。

複数の方向余弦が取り扱われる時にはｌ，ｍ，ｎなどの文字によって方向余弦が書かれる事もありますが、ここでは普通の余弦として表記しています。

証明

第１式の証明は内積を使います。また、第１式から第２式を証明できます。

ベクトルの成分表示を方向余弦を使って書き、内積をとります。

\(\overrightarrow{A}\) ＝（A１，A２，A３）＝A (cosθｘ，cosθｙ，cosθｚ)
\(\overrightarrow{B}\) ＝（B１，B２，B３）＝B (cosωｘ，cosωｙ，cosωｚ)
\(\overrightarrow{A}\cdot\overrightarrow{B}\)＝AB (cosθｘcosωｘ＋cosθｙcosωｙ＋cosθｚcosωｚ)

他方で\(\overrightarrow{A}\cdot\overrightarrow{B}\)＝AB cosφ なので、
AB cosφ＝AB (cosθｘcosωｘ＋cosθｙcosωｙ＋cosθｚcosωｚ)
A＞０かつB＞０よりAB＞０なので
cosφ＝cosθｘcosωｘ＋cosθｙcosωｙ＋cosθｚcosωｚ

次に２式目については、Acosφ＝B の関係式に１式目の結果を代入します。
A cosθｘ＝Aｘ等の関係を使って途中の変形を行います。

B＝Acosφ
＝A (cosθｘcosωｘ＋cosθｙcosωｙ＋cosθｚcosωｚ)
＝(A cosθｘ) cosωｘ＋(A cosθｙ) cosωｙ＋(A cosθｚ) cosωｚ
＝Aｘcosωｘ＋ A ｙcosωｙ＋Aｚcosωｚ

この２式目のほうの式は、次に見て行くように２つの直交座標においてベクトルの成分の変換公式を導出するのに必要です。（直交座標から直交曲線座標への変換も局所的には可です。）

公式３：２つの直交座標系でのベクトル成分の変換公式

原点を共有する２つの異なる直交座標を考えます。１つの直交座標に対して、もう片方の直交座標が原点を共有した状態で回転したような位置関係です。
この時のベクトルの成分に対する座標変換に対して、方向余弦を使う事ができます。

ここで言う「ベクトルの成分に対する座標変換」とは、
１つの直交座標における成分で表されたベクトルが、空間での大きさと向きは同じにしたままで
「別の直交座標から見た時」にはどのような成分で書けるだろうか？という問題です。

得られる公式は形が規則的ではあるのですが、３軸の３軸に対する方向余弦を考える必要があるので合計９個の方向余弦を必要とします。
それらは１～３の番号の組み合わせを使うと処理をしやすい場合もありますが
（線形変換的な式なので、特に行列などを使う場合など）、
ここではｘ，ｙ，ｚとＸ，Ｙ，Ｚの文字で区別を行う事にします。

原点を共有する２つの直交座標間の変換公式

原点を共有するｘｙｚ系とＸＹＺ系の２つの直交座標軸があり、
片方はもう片方に対して原点回りに回転したような位置配置となっているとします。
この時にｘ，ｙ，ｚの軸上のベクトルからＸ，Ｙ，Ｚの軸への方向余弦を考えます。
ｘ軸上のベクトルに対するＹ軸への方向余弦を cosθｘＹのように書く事にすると、
ｘｙｚ座標系で成分を考えたベクトル\(\overrightarrow{A}\) ＝（Aｘ，Aｙ，Aｚ）（\(\neq\overrightarrow{0}\)）を
XYZ座標系の成分（AX，AY，AX）で書く時の変換の式は次のようになります。

  • AX＝AｘcosθXｘ ＋AｙcosθXｙ ＋AｚcosθXｚ
  • AY＝AｘcosθYｘ ＋AｙcosθYｙ ＋AｚcosθYｚ
  • AZ＝AｘcosθZｘ ＋AｙcosθZｙ ＋AｚcosθZｚ

また、逆にXYZ座標系の成分で書かれた（AX，AY，AX）を
ｘｙｚ座標系の成分（Aｘ，Aｙ，Aｚ）で書くには次のような変換をします。

  • Aｘ＝AXcosθXｘ ＋AYcosθYｘ ＋AZcosθZｘ
  • Aｙ＝AXcosθXｙ ＋AYcosθYｙ ＋AZcosθZｙ
  • Aｚ＝AXcosθXｚ ＋AYcosθYｚ ＋AZcosθZｚ

後述しますが、２つの異なるベクトルに対してこの変換を適用した時に
２つのベクトルの内積は変換前と変換後で値は同じ（＝不変）になります。
（そこから前提である２つのベクトルの大きさも変換の前後で値は同じという事も見れます。）

ここでも考えているベクトルはゼロベクトルを除いていますが、考えている２つの直交座標系は原点を共有しているという設定なので、原点におけるゼロベクトルはそもそも変換の必要はなくどちらの座標系でも同じ成分（０，０，０）として共有されている事になります。

上記の変換の３式は線形結合の形なので、次のように行列の積で表現する事もできます。
また、方向余弦の添え字が一定の規則性を持つので行と列に上手く対応させる事ができます。 $$ \left(\begin{array}{c} A_X\\ A_Y\\ A_Z\end{array}\right) = \left(\begin{array}{lcr} \cos\theta_{Xx} &\cos\theta_{Xy}&\cos\theta_{Xz}\\ \cos\theta_{Yx} &\cos\theta_{Yy}&\cos\theta_{Zy}\\ \cos\theta_{Zx} &\cos\theta_{Yz}&\cos\theta_{Zz}\end{array}\right) \left(\begin{array}{c} A_x\\ A_y\\ A_z\end{array}\right) $$ ３行３列程度ならわざわざ行列にするよりも普通に式で書く方が早いし分かりやすいと見るか、
行列で見たほうが規則性が明らかで書く手間も少し減ると見るかは人それぞれと思われます。

９つの方向余弦の位置関係を表にして整理すると次のようになります。

方向余弦X軸からY軸からZ軸から
ｘ軸へcosθXｘcosθYｘcosθZｘ
ｙ軸へcosθXｙcosθYｙcosθZｙ
ｚ軸へcosθXｚcosθYｚcosθZｚ
方向余弦の添え字が規則的で、式が線形結合の形なので行列の積で関係式を書く事もできます。また、ここでのアルファベットの添え字を番号に変えると行列の行と列の番号に対応させる事もできます。

余弦が角度のプラスマイナスで同じ値になる事を考えると、これらの方向余弦は「ｘｙｚ系の軸からＸＹＺ系の軸への方向余弦」を考えた時と同じ値になります。つまり例えば「ｚ軸からＹ軸への方向余弦」は「Z軸からｙ軸への方向余弦cosθZｙ」と同じものを使ってよいという事です。
ただしｘｙｚ系の軸からＸＹＺ系変換への公式は導出過程に由来して、
単純にｘ，ｙ，ｚとＸ，Ｙ，Ｚの置き換えをすればよいわけではなく
「ｘ軸から考えた場合の３つの方向余弦」を使う必要があります。
表で言うと、
ＸＹＺ系への変換では１つの変換につき「縦」の３つを使うのに対して、
ｘｙｚ系への変換では１つの変換につき「横」の３つを使う事になります。

ここで具体的な角度よりも「余弦の値」自体のほうが基本的に重要となる事を考えて、
方向余弦を cosθＸｙ＝CXｙのように略記すると次のように書けます。

方向余弦X軸からY軸からZ軸から
ｘ軸へCXｘCYｘCZｘ
ｙ軸へCXｙCYｙCZｙ
ｚ軸へCXｚCYｚCZｚ

さらに、添え字をアルファベットではなく１～３の番号だけで書くと次のようになります。

方向余弦X軸からY軸からZ軸から
ｘ軸へC１１C１２C１３
ｙ軸へC２１C２２C２３
ｚ軸へC３１C３２C３３

変換後の式が線形変換の形になっている事に由来して方向余弦の配列を行列として扱う時には、添え字の組み合わせと行・列の番号が一致するので便利な事もあります。また、和をシグマ記号で表したい時も添え字がアルファベットではなく番号になっているほうが便利です。
ただし２種類の添え字を同じ１～３の番号で表すと、どの軸からどの軸への方向余弦を考えているかといった図的な位置関係は少し見えにくくなります。そのため、この記事では番号ではなくアルファベットによる添え字を使用しています。いずれの表示方法でも表現する事自体は同じです。

この公式の変換は原点を始点として考えていますが、任意の点を始点とする場合でもそこを基準に考えるかベクトルを原点に平行移動して考える事によって変換公式を適用する事ができます。直交座標系ではベクトルの向き（および大きさ）を保ったまま平行移動を行っても軸とのなす角は同じ値に保たれます。つまり方向余弦の値も同じものが使えるので、上記の変換公式を適用できます。

証明

変換公式の証明には前述の「ベクトルの直線への射影と方向余弦の関係式」を使います。本質的には、意味を把握しているならその関係式に当てはめる事で変換の式はそのまま導出できます。

（再掲）ベクトルの直線への射影と方向余弦の関係式

前述の公式を書くと次の通りです。
ここでは射影ベクトルの始点からの距離を表すほうの式だけを使います。 $$\large{B=A_x\cos\omega_x+A_y\cos\omega_y+A_z\cos\omega_z}$$ 変換公式の証明用に変数を対応させると次のようになります。 $$\large{A_X=A_x\cos\theta_{Xx}+A_y\cos\theta_{Xy}+A_z\cos\theta_{Xz}}$$ 実はこれで変換公式の証明に既になってしまっているのですが、
以下もう少し詳しく説明を加えます。

まず、ｘｙｚ系からXYZ系への変換を考えたいので
「ＡＸをAｘ，Ａｙ，Ａｚと方向余弦で表す」事を考えます。
そこで、ベクトル\(\overrightarrow{A}\)のＸＹＺ系の各軸への射影を１つずつ考えます。
すると、ベクトルの終点から軸に下ろした垂線の足と始点までの距離は、
実はそれがそのまま「ＸＹＺ系における座標成分」になっています。

すると「X軸からのｘ軸」「X軸からのｙ軸」「X軸からのｚ軸」への方向余弦を考えて、公式に当てはめればXYZ系でのベクトル\(\overrightarrow{A}\)の「X成分」が得られるという流れです。
それが AX＝AｘcosθXｘ ＋AｙcosθXｙ ＋AzcosθXｚの式になります。

Y軸についても同様に「Y軸からのｘ軸」「Y軸からのｙ軸」「Y軸からのｚ軸」への方向余弦を考え、
Z軸についても同様に「Z軸からのｘ軸」「Z軸からのｙ軸」「Z軸からのｚ軸」への方向余弦を考えて
AY＝AｘcosθYｘ ＋AｙcosθYｙ ＋AｚcosθYｚ および
AZ＝AｘcosθZｘ ＋AｙcosθZｙ ＋AｚcosθZｚ の式を得ます。

逆変換の式の場合

同じ考え方で、XYZ系の成分で表されたベクトルをｘｙｚ系の成分で表す逆変換の式も作れます。
ただし「考え方」が同じでも使う方向余弦が違ってくるので注意も必要です。【余弦の値自体はｘ軸からＹ軸の方向余弦はＹ軸からｘ軸への方向余弦と同じものを使えます。cosθ＝cos(－θ)であるため。】

ｘｙｚ系からの変換を考える時には、使う方向余弦は次のようになります。

Aｘを表すために使う方向余弦Aｙを表すために使う方向余弦Aｚを表すために使う方向余弦
「ｘ軸からX軸」cosθXx
「ｘ軸からY軸」cosθYx
「ｘ軸からZ軸」cosθZx		「ｙ軸からX軸」cosθXｙ
「ｙ軸からY軸」cosθYｙ
「ｙ軸からZ軸」cosθZｙ		「ｚ軸からX軸」cosθXｚ
「ｚ軸からY軸」cosθYｚ
「ｚ軸からZ軸」cosθZｚ

XYZ系からの変換の時とは微妙に違っていて、各変換の式で使用する方向余弦のうち１つは共通していて残り２つは異なっています。（行列表示で言えばcosθXxなどの対角成分は共通していて、残り２つが違うものになっています。）

式で使うベクトル\(\overrightarrow{A}\)の成分についてはXYZ系での成分であるAｘ，Ａｙ，Ａｚを使用します。
これらによって、ｘｙｚ系での成分であるAｘ，Aｙ，Aｚを表す式を得るわけです。

すなわち
Aｘ＝AXcosθXｘ ＋AYcosθYｘ ＋AZcosθZｘ
Aｙ＝AXcosθXｙ ＋AYcosθYｙ ＋AZcosθZｙ
Aｚ＝AXcosθXｚ ＋AYcosθYｚ ＋AZcosθZｚ の３式が導出されます。

局所的には直交曲線座標への変換にも適用可能である件

上記の方向余弦による直交座標間のベクトルの変換公式は、
局所的には極座標や球面座標などの「直交曲線座標」にも適用可能です。
その事についてもここで簡単に触れておきます。

ここで「局所的に」というのは、直交曲線座標においては１つ１つの点において２つまたは３つの座標曲線（極座標だと同心円と放射状に伸びる直線）の接線ベクトルが互いに直交するので、そこに限定して見れば「直交座標とみなせる」という事を指します。

ただし直交曲線座標では一般的に、そのような局所的には直交座標の軸とみなせる接線ベクトルも位置を変えれば向きが変わってしまいます。ですので直交曲線座標においては「向きが異なる局所的な直交座標」が至るところに存在するという感じです。

そのため、直交曲線座標に対して上記の変換公式を使う時には方向余弦を微分や偏微分を使って表します。そのようにする事で、変換の式が座標変数による関数として表せるので、結果的に領域全体での変換を表す事が可能になります。これは微分方程式に対して基本ベクトルを変更する形での極座標変換を行う時などに重要になります。

基本ベクトルを変更しない形での微分方程式の極座法変換もあり、その場合には方向余弦を使った公式は不要になります。
方向余弦を使った変換公式を適用する必要があるのは力ベクトルなども含めたベクトル場の成分をｘ，ｙ，ｚではなくｒ，θ，φで表し、ｒやθによる変化を考えたい場合です。

直交座標から直交曲線座標へのベクトルの成分の変換を行う時には方向余弦を微分や偏微分によって表す事になります。微積分・ベクトル解析的な考察は多少必要ですが、方向余弦による変換の公式自体は直交座標同士の変換の場合と同じ形で考える事ができます。図で、方向余弦はCの文字と添え字によって略記しています。
直交曲線座標への変換での方向余弦の具体的な関数形は表し方が２通りあり、いずれも微分・偏微分によって表されます。

公式４：直交座標変換における方向余弦の関係式

上記は９つの方向余弦を使った「成分についての座標変換の公式」でしたが、
９つの方向余弦自体に対して成立する関係式も公式として存在します。

直交座標の変換における方向余弦同士の関係式

■ J，K ＝X，Y，Z のそれぞれ（J≠K）に対して次式が成立します。
$$\large{ \cos\theta_{Jx}\cos\theta_{Kx}+\cos\theta_{Jy}\cos\theta_{Ky}+\cos\theta_{Jz}\cos\theta_{Kz}=0 }$$ ■ ｊ＝x,y,z のそれぞれに対して次式が成立します。 $$\large{ \cos^2\theta_{Xj}+\cos^2\theta_{Yj}+\cos^2\theta_{Zj}=1 }$$ ■ j, k ＝ x,y,z のそれぞれ（j≠ｋ）に対して次式が成立します。
【ｊ＝ｋの時は第２式になります。】 $$\large{ \cos\theta_{Xj}\cos\theta_{Xk}＋\cos\theta_{Yj}\cos\theta_{Yk}＋\cos\theta_{Zj}\cos\theta_{Zk}=0 }$$ ■J＝X，Y，Z のそれぞれに対して次式が成立します。
（第１式の左辺でJ＝Kとした時に相当。） $$\large{ \cos^2\theta_{Jx}+\cos^2\theta_{Jy}+\cos^2\theta_{Jz}=1 }$$ J≠Kおよびｊ≠ｋのもとで
第１式の意味は「XYZ系の２つの軸からのｘｙｚ系の１つの軸への方向余弦の積の和は０になる」
第２式の意味は「ｘｙｚ系の１つの軸からのXYZ系の各軸への方向余弦の２乗和は１になる」
第３式の意味は「ｘｙｚ系の２つの軸からのXYZ系の１つの軸への方向余弦の積の和は０になる」
という事になります。
第３式でｊ＝ｋとした場合が第２式、
第１式でＪ＝Ｋとした場合が第４式であり、値が変わる事になります。
（ｊ＝ｋとｊ≠ｋおよびＪ＝ＫとＪ≠Ｋの場合分けで全体を２式にまとめる事もできます。）
第２式と第４式は、空間内の直交座標系の任意のベクトルに対して「各軸への方向余弦の２乗和は１になる」という公式と実は同じものであるという見方もできます。

これらの公式は「暗記」するようなものではなく、このような規則的な関係が成立するという認識のもと、もし必要であれば適宜参照すればよいと考えるべきでしょう。後述する「原点を共有する直交座標間の変換の前後でベクトルの内積は不変である」事の証明ではこれらの関係式の一部を使います。

この図での各方向余弦は、略記で記しています。公式が表す結果で考えると、要するに和を考えると０になる関係式と１になる関係式がそれぞれ２つずつ、計４つ存在します。ｘｙｚ系の軸とＸＹＫ系の軸の対応関係から整理すると比較的見やすいかもしれません。

$$ \left(\begin{array}{c} A_X\\ A_Y\\ A_Z\end{array}\right) = \left(\begin{array}{lcr} \cos\theta_{Xx} &\cos\theta_{Xy}&\cos\theta_{Xz}\\ \cos\theta_{Yx} &\cos\theta_{Yy}&\cos\theta_{Zy}\\ \cos\theta_{Zx} &\cos\theta_{Yz}&\cos\theta_{Zz}\end{array}\right) \left(\begin{array}{c} A_x\\ A_y\\ A_z\end{array}\right) =\left(\begin{array}{lcr} C_{11} &C_{12}&C_{13}\\ C_{21} &C_{22}&C_{23}\\ C_{31} &C_{32}&C_{33}\end{array}\right) \left(\begin{array}{c} A_x\\ A_y\\ A_z\end{array}\right)$$ のように方向余弦を略記して、さらに行列の要素に対応する番号で表す時には
上記の公式は次のようにも書けます。 $$\sum_{n=1}^3C_{Jn}C_{Kn}=0\hspace{5pt}(J\neq K)$$ $$\sum_{n=1}^3(C_{nj})^2=1$$ $$\sum_{N=1}^3C_{Nj}C_{Nk}=0\hspace{5pt}(j\neq k)$$ $$\sum_{n=1}^3(C_{Jn})^2=1$$ （J，K＝１，２，３は、ここでは行の番号です。ｊ，ｋ＝１，２，３はここでは列の番号。）

公式例行列要素での表記
　cosθJｘcosθKｘ
＋cosθJｙcosθKｙ
＋cosθJｚcosθKｚ＝０
（J≠Kの時）		　cosθXｘcosθZｘ
＋cosθXｙcosθZｙ
＋cosθXｚcosθZｚ＝０
【X，Z軸からの方向余弦の積の和】		$$\sum_{n=1}^3C_{Jn}C_{Kn}=0\hspace{5pt}(J\neq K)$$
　cos２θＸｊ
＋cos２θＹｊ
＋cos２θＺｊ＝１
（第３式でｊ＝ｋの時）		　cos２θＸｙ
＋cos２θＹｙ
＋cos２θＺｙ＝１
【ｙ軸への方向余弦の２乗和】		$$\sum_{n=1}^3(C_{nj})^2=1$$
　cosθXｊcosθXｋ
＋cosθYｊcosθYｋ
＋cosθZｊcosθZｋ＝０
（j≠kの時）		　cosθXｘcosθXｚ
＋cosθYｘcosθYｚ
＋cosθZｘcosθZｚ＝０
【ｘ，ｚ軸への方向余弦の積の和】		$$\sum_{N=1}^3C_{Nj}C_{Nk}=0\hspace{5pt}(j\neq k)$$
　cos２θJｘ
＋cos２θJｙ
＋cos２θJｚ＝０
（第１式でJ＝Kの時）		　cos２θZｘ
＋cos２θZｙ
＋cos２θZｚ＝０
【Z軸からの方向余弦の２乗和】		$$\sum_{n=1}^3(C_{Jn})^2=1$$

証明

証明はいずれも内積計算を使いますが、２乗和の形の式はそれ以外の方法でもできます。
ここで考えるベクトルは任意のベクトルではなく「始点と終点が軸上にあるベクトル」です。
以下、そのようなベクトルを「軸に重なるベクトル」と呼ぶ事にします。
１つの座標系における軸に重なるベクトルであっても、別の座標系から見た成分で書くと通常のベクトルとして扱われる事になり、その事をここでの証明でも使います。

第１式

第１式については、X，Y，Z軸の異なる２つの軸は直交しますから、それらの軸上のベクトル同士の内積は０です。そこで、ベクトルの成分で内積を計算して０に等しいとする事で証明されます。（同じ１つの軸同士【公式でJ=K】であれば当然直交はせず、内積は大きさの２乗になります。それは第４式の証明です。）

J≠Kの時に J 軸と K 軸（例えばX軸とZ軸）は直交するので、
大きさが P（＞０）のJ軸上のベクトル\(\overrightarrow{P}\)について成分はｘｙｚ系での座標で書ける事に注意すると
\(\overrightarrow{P}\)＝ P (cosθJｘ，cosθJｙ，cosθJｚ)
同じように大きさがQ（＞０）であるK軸に重なるベクトル\(\overrightarrow{Q}\) は次のように書けます。
\(\overrightarrow{Q}\)＝ Q (cosθKｘ，cosθKｙ，cosθKｚ)
２つのベクトルは直交するので内積は０であり、
\(\overrightarrow{P}\cdot\overrightarrow{Q}\)＝PQ(cosθJｘcosθKｘ＋cosθJｙcosθKｙ＋cosθJｚcosθKｚ)＝０
PQ≠０なので J≠K であれば
cosθJｘcosθKｘ＋cosθJｙcosθKｙ＋cosθJｚcosθKｚ＝０

第２式

第２式については、ｘｙｚ系の軸に重なるベクトルから見て考えます。
ｘｙｚ系のｊ軸（例えばy軸）に重なる大きさ（ｐ＞０）のベクトル\(\overrightarrow{p}\)を考えて、
成分をXYZ系の座標として書きます。
方向余弦はXYZ系からｘｙｚ系へのものを選んで使う事ができ、
ｋ軸からＸ，Ｙ，Ｚに向かうものを選ぶ事に注意すると次のように書けます。
\(\overrightarrow{p}\)＝ ｐ (cosθXｊ，cosθYｊ，cosθZｊ)
同じベクトル同士の内積\(\overrightarrow{p}\cdot\overrightarrow{p}\)を考えるか、
成分で計算したベクトルの大きさ＝ｐ２と考える事で結果の式を得ます。
\(\overrightarrow{P}\cdot\overrightarrow{P}\)＝ｐ２(cos２θXｊ＋cos２θYｊ＋cos２θZｊ)＝ｐ２
ｐ＞０なので
cos２θXk＋cos２θYk＋cos２θZk＝１

この式は第３式でｊ＝ｋとして考えた場合でもあります。

第３式

第３式はｘｙｚ系から見て、第１式の時と同じように考えます。
ｊ，ｋ＝ｘ，ｙ，ｚでｊ≠ｋのもとで、ｐ＞０およびｑ＞０が大きさである
ｊ軸とｋ軸に重なる２つのベクトルを考えると、２つのベクトルは直交します。
両者をＸＹＺ系の座標で書き、内積を成分で計算して０になるとおくと結果の式を得ます。
\(\overrightarrow{p}\)＝ ｐ(cosθXj，cosθYj，cosθZj)
\(\overrightarrow{q}\)＝ ｑ (cosθXk，cosθYk，cosθZk)
\(\overrightarrow{p}\cdot\overrightarrow{q}\)＝ｐｑ(cosθXjcosθXk＋cosθYjcosθYk＋cosθZjcosθZk)＝０
ｐ＞０かつｑ＞０なのでｊ≠ｋであれば
cosθXjcosθXk＋cosθYjcosθYk＋cosθZjcosθZk＝０

第４式

第４式は、第１式において大きさがP （＞０）の１つのベクトル同士の内積か大きさを成分で計算する事で結果の式を得ます。
\(\overrightarrow{P}\cdot\overrightarrow{P}\)＝P２(cos２θJｘ＋cos２θJｙ＋cos２θJｚ)＝P２
P＞０なので
cos２θJｘ＋cos２θJｙ＋cos２θJｚ＝１

第２式と第３式はｘｙｚ系から見て計算を考えましたが、得られた方向余弦の関係式はＸＹＺ系をｘｙｚ系に変換する場合でも成立しているので必要があれば使ってもよい事になります。
また、第２式と第４式に関しては成分を考えている座標系だけから見れば「ある１つのベクトル」を考えている事になります。そのため、前述の「方向余弦の２乗和は１になる」という公式と実は同じものであるという見方もできます。

方向余弦を使った直交座標の変換の前後において内積は不変である事の証明

座標変換をした時に値が変わらない量（「不変量」）についての考察は数学的に重要で、扱う対象によっては物理学でも重要となる場合もあります。

ところで前述の原点を「共有する直交座標同士のベクトルの成分の変換」は、ベクトル自体はいじっていないはずなので変換前と変換後で大きさは「同じはず」です。もしも、現に計算したらベクトルの大きさの値が変わってしまうなどという結果が出たら整合性がとれず困った事になります。
しかし実際は計算をしてもベクトルの大きさは同じ値に保たれる事が数式でも分かります。
そして実は、変換前と変換後ではベクトルの大きさだけでなく内積が同じ値に保たれているのです。

方向余弦を使った座標変換の前後における内積

２つのベクトルの成分を、原点を共有する２つの直交座標間で変換するとします。
\(\overrightarrow{A}\) ＝（Aｘ，Aｙ，Aｚ）および\(\overrightarrow{B}\) ＝（Bｘ，Bｙ，Bｚ）を考えて、
変換後の座標はそれぞれ
（AX，AY，AZ）および（BX，BY，BZ）であるとします。
この時に２つのベクトルの内積\(\overrightarrow{A}\cdot\overrightarrow{B}\) の値は、変換前のｘｙｚ系の座標成分で計算しても、
変換後の座標成分で計算しても同じ値になります。 $$\overrightarrow{A}\cdot\overrightarrow{B}=A_xB_x+A_yB_y+A_zB_z=A_XB_X+A_YB_Y+A_ZB_Z$$ 同じベクトル同士の内積を考える事により、
変換の前後でベクトルの大きさも同じ値に保たれる事も確認される事になりす。
（外積ベクトルについては変換によって異なるベクトルに変化してしまいます。）

証明

変換後の成分で内積を計算し、変換前の内積の値に等しくなる事を示します。

２つのベクトルの変換について、使用する方向余弦は「座標軸から座標軸へのもの」なので共通して使う事ができます。

  • AX＝AｘcosθXｘ ＋AｙcosθXｙ ＋AｚcosθXｚ
  • AY＝AｘcosθYｘ ＋AｙcosθYｙ ＋AｚcosθYｚ
  • AZ＝AｘcosθZｘ ＋AｙcosθZｙ ＋AｚcosθZｚ
  • BX＝BｘcosθXｘ ＋BｙcosθXｙ ＋BｚcosθXｚ
  • BY＝BｘcosθYｘ ＋BｙcosθYｙ ＋BｚcosθYｚ
  • BZ＝BｘcosθZｘ ＋BｙcosθZｙ ＋BｚcosθZｚ

さて、これの内積を計算するとなるとX成分だけで見ても９つの項ができる事になりますが
規則性があるので全体としても３項の和の塊が９つという形です。
さらに前述の座標変換時の方向余弦に関する関係式を使うと、実は多くの部分が０になるのです。

  1. AｘBｘcos２θXｘ＋AｘBｘcos２θYｘ＋AｘBｘcos２θZｘ＝AｘBｘ
    【∵cos２θXｘ＋cos２θYｘ＋cos２θZｘ＝１】
  2. AｘBｙcosθXｘcosθXｙ＋AｘBｙcosθYｘcosθYｙ＋AｘBｙcosθZｘcosθZｙ＝０
    【∵cosθXｘcosθXｙ＋cosθYｘcosθYｙ＋cosθZｘcosθZｙ＝０】
  3. AｘBｚcosθXｘcosθXｚ＋AｘBｚcosθYｘcosθYｚ＋AｘBｚcosθZｘcosθZｚ＝０
    【∵cosθXｘcosθXｚ＋cosθYｘcosθYｚ＋cosθZｘcosθZｚ＝０】
  4. AｙBｙcos２θXｙ＋AｙBｙcos２θYｙ＋AｙBｙcos２θZｙ＝AｙBｙ
    【∵cos２θXｙ＋cos２θYｙ＋cos２θZｙ＝１】
  5. AｙBｘcosθXｙcosθXｘ＋AｙBｘcosθYｙcosθYｘ＋AｙBｘcosθZｙcosθZｘ＝０
    【∵cosθXｘcosθXｙ＋cosθYｘcosθYｙ＋cosθZｘcosθZｙ＝０（２番目の計算と同じ）】
  6. AｙBｚcosθXｙcosθXｚ＋AｙBｚcosθYｙcosθYｚ＋AｙBｚcosθZｙcosθZｚ＝０
    【∵cosθXｙcosθXｚ＋cosθYｙcosθYｚ＋cosθZｙcosθZｚ＝０】
  7. AｚBｘcosθXｚcosθXｘ＋AｚBｘcosθYｚcosθYｘ＋AｚBｘcosθZｚcosθZｘ＝０
    【∵cosθXｘcosθXｚ＋cosθYｘcosθYｚ＋cosθZｘcosθZｚ＝０（３番目の計算と同じ）】
  8. AｚBｙcosθXｚcosθXｙ＋AｚBｙcosθYｚcosθYｙ＋AｚBｙcosθZｚcosθZｙ＝０
    【∵cosθXｙcosθXｚ＋cosθYｙcosθYｚ＋cosθZｙcosθZｚ＝０（６番目の計算と同じ）】
  9. AｚBｚcos２θXｚ＋AｚBｚcos２θYｚ＋AｚBｚcos２θZｚ＝AｚBｚ
    【∵cos２θXｚ＋cos２θYｚ＋cos２θZｚ＝１】

ここでは一応全部記してみましたが、
「２番目と５番目」「３番目と７番目」「６番目と８番目」は
掛け合わせる方向余弦の順番が違うだけで実質的に同じ計算であり、しかも値が０になります。
つまり６式については実は３組のほぼ同じ計算の式で、しかも０になって消えるわけです。
残るのは他の３つだけで、それらは方向余弦の部分が上手い具合に１になります。
よって、XYZ系に成分を変換後の内積の値は
AｘBｘ＋AｙBｙ＋AｚBｚとなり、
これは変換前の内積の値に一致するわけです。

シグマ記号で計算する場合、１～３の番号を使った処理も可能です。

XYZ系からｘｙｚ系への逆変換の式でも、内積の不変性は同様に証明も同様に可能です。

乗じる項の順番が異なるだけで実質的に同じ計算になる２組の箇所が３つあったのはあながち偶然ではなくて、実は行列の非対角部分でＣ１２とＣ２１のような転置の配置にある要素の組がそれらに該当します。
また、計算結果が０にならなかった部分は対角部分の３つです。
ここでの変換の場合に方向余弦が行列の要素に対応するような結果の式であったので、そのような規則性が見れるわけです。

上記の証明について、シグマ記号を使った証明も記します。
番号を使ってやる事も可能ですが、ここではアルファベットのままやる方法を書きます。
方向余弦はcosθXｚ＝CXｚのような略記号を使います。$$\large{\overrightarrow{A}\cdot\overrightarrow{B}＝\sum_{J=X,Y,Z}A_JB_J}$$ $$\large{=\sum_{J=X,Y,Z}\left\{\left(\sum_{j=x,y,z}C_{Jj}A_j\right)\left(\sum_{k=x,y,z}C_{Jk}B_k\right)\right\}}$$ $$\large{=\sum_{J=X,Y,Z}\left(\sum_{j,k=x,y,z}C_{Jj}C_{Jk}A_jB_k\right)}$$ $$\large{=\sum_{j,k=x,y,z}\left\{A_jB_k\left(\sum_{J=X,Y,Z}C_{Jj}C_{Jk}\right)\right\}}$$ この式をよく見ると、１つのJを決めてｊ，ｋ＝ｘ，ｙ，ｚについて加え合わせた時に、
前述の公式によりｊ＝ｋの場合以外は０になる事が分かります。 $$j\neq kの時、\large{ \cos\theta_{Xj}\cos\theta_{Xk}＋\cos\theta_{Yj}\cos\theta_{Yk}＋\cos\theta_{Zj}\cos\theta_{Zk}=0なので、 }$$ $$j\neq kの時、\large{A_jB_k\left(\sum_{J=X,Y,Z}C_{Jj}C_{Jk}\right)=0}$$ よって内積はｋ＝ｊの項だけ考えればよい事になりますが、
ｋ＝ｊの時は同じ形の式が１になるので結局、方向余弦は全て式から無くなります。
整理すると、次のようになります。 $$ \large{\overrightarrow{A}\cdot\overrightarrow{B}=\sum_{j=x,y,z}\left\{A_jB_j\left(\sum_{J=X,Y,Z}C_{Jj}C_{Jj}\right)\right\}} $$ $$\large{=\sum_{j=x,y,z}\left(A_jB_j\right)}$$ これによってXYZ系の成分による内積の結果と、
ｘｙｚ系の成分による内積の結果が等しい事が示されます。

逆三角関数

恭平

逆三角関数とは「三角関数の逆関数」で、正弦、余弦、正接のそれぞれに対して存在し、
それぞれ「逆正弦関数」「逆余弦関数」「逆正接関数」と呼んで Arcsinｘ，Arccosｘ，Arctanｘ
もしくは sin－１ｘ，cos－１ｘ，tan－１ｘ のように書きます。
あるいは arcsinｘ，arccosｘのように書く事もできますが、
それらは記述法によっては Arcsinｘ等と区別して意味を持たせる事もあります。

逆三角関数が使われる事が比較的多いのは微積分においてです。そのため、この記事の後半では微積分的な内容がやや多くなります。また、どちらかというと数学的な内容が中心になりますが逆三角関数のいくつかの使用例についても説明します。

※三角関数のベキ乗は、習慣的に(sinｘ)2＝sin2ｘのように書かれます。
しかし、一般的にはsin－１ｘは逆正弦関数（＝正弦関数の逆関数）であって、
１／(sinｘ)を意味しない事が多いです。
一般的に、三角関数の逆数に関しては１／(sinｘ)＝(sinｘ)－１（＝cosecｘ） と書き、
負のベキ乗（あるいは逆数のベキ乗）に関しては
{１／(sinｘ)}2＝１／(sin2ｘ)＝(sinｘ)－２（＝cosec2ｘ）などのように書きます。
一般的に、ｆ(ｘ)の逆関数はｆ－１(ｘ)と記します。
表記体系としては一応 sin－１ｘを１／sinｘと勘違いしないようにはなっていますが、
当サイトでは基本的に逆三角関数は Arcsinｘや Arccosｘの表記を使用しています。

また、「余接（cot）」「正割(sec)」「余割(cosec)」などは三角関数の「逆数」です。
例えばsecθ＝１／(cosθ)であって、それらは「逆三角関数」とは別物になります。
余接関数等にも逆関数を考える事はできますが、正弦・余弦・正接の逆三角関数と比べると使用頻度は低いと言えます。

種類と基本的性質

通常の正弦関数ｙ＝sinｘに対してはｘの値を決めればｙが定まるわけですが、理論的にはｙに対してｘの値も計算できるというふうにも見れます。つまりｘ＝f(ｙ) のように考えるわけです。これが一般的な逆関数の考え方ですが、それを三角関数について考えたものが逆三角関数です。

逆三角関数（三角関数の逆関数）
  • ｙ＝sin ｘの時、ｘ＝Arcsinｙ（もしくはsin －１ｙ）と書き、逆正弦関数と呼びます。
  • ｙ＝cosｘの時、ｘ＝Arccosｙ（もしくはcos－１ｙ）と書き、逆余弦関数と呼びます。
  • ｙ＝tanｘの時、ｘ＝Arctanｙ（もしくはtan－１ｙ）と書き、逆正接関数と呼びます。

Arcsinｘと書く場合は、「アークサインエックス」のようにも読む事があります。
同様にArccos, Arctan は「アークコーサイン」「アークタンジェント」と読みます。

例えばｙ＝sinｘに対して
ｘ＝π／２の時にはｙ＝sin(π／２)＝１であるので、π／２＝Arcsin１のようになります。
同様に、例えばｘ＝π／４の時にtanｘ＝１なので π／４＝Arctan１のようになります。
つまり「三角関数あるいは三角比のある値を与える角度は何か？」
という事を表したのが逆三角関数です。

逆三角関数は通常の三角関数と違って、微積分に関して以外の関係式は多くありません。
例えば加法定理のような関係式は基本的に考えないわけです。（ただし通常の三角関数の加法定理と組み合わせて計算をする事はあります。）
積分の時に一応覚えていると良いかもしれない関係式としては
Arcsinｘ＋Arccosｘ＝π／２があります。
ただしこれは後述するように
逆三角関数の値として「主値」を採用する場合において成立するものです。
すなわち、Arcsinｘの値域を [－π／２，π／２]として
Arccosｘの値域を [０，π]とした場合に成立する関係式です。

ですので具体的な意味としては実は難しくないのですが、
数学的には注意点は２つほどあります。

逆三角関数についての数学上の重要な注意点
  • 逆三角関数を単独の関数として扱う時は、他の関数と同じく「ｘを変数として」
    ｙ＝Arcsinｘのように書くのが普通です。（その時、sinｙ＝ｘです。）
    通常の三角関数ｙ＝sinｘに対して逆正弦関数を考えるならｘ＝Arcsinｙとも書きます。
    ただし文字自体は変数をｘとしてもｙとしても、本質的にはどちらでも変わりません。
  • 三角関数は周期関数なので
    ｙ＝sinｘなどにおいてｙの値に対して複数の（無限個の）ｘの値があり得ます。
    例えばｘ＝π／４の時にtanｘ＝１となるのは「ｘ＝π／４もそうだがｘ＝９π／４もそうである」といった話にもなるという事です。
    そのために逆三角関数を考える時には通常、１周期分だけを考えて
    特に０を含む値域（三角関数で言えば定義域）を単調関数になるように選んで使うのが普通です。逆三角関数がその範囲の値である事を指して主値と呼びます。

ｙとｘの文字の使い分けの関係は混乱を生じやすいかもしれませんが、
何の文字を使っているかに関わらずに Arcsin 等の逆三角関数を使う時には
変数とその定義域は「通常の三角関数の値」であり、
逆三角関数の値とその値域は「角度」を考えています。

多くの場合、三角関数ｙ＝sinｘなどを使っている中で逆三角関数を考える場合には
変数と関数を表す文字を区別するためにｘ＝Arcsinｙのように書いて、
微積分などで単独で逆三角関数を最初から使う時にはｙ＝Arcsinｘのように書いたりします。
（後述で少し触れますが同じく逆関数の関係にある指数関数と対数関数の関係と同じように捉えると分かりやすいかもしれません。）

文字としてはｘでなくてもθなどを使っても同じです。

逆三角関数の「主値」について

逆三角関数の変数の定義域および値域としての「三角関数の１周期分」については無限個の区間からどこを切り取っても同じですが、普通は逆三角関数が単調増加または単調減少となるように考えます。
例えば sinx に対しては [－π／２，π／２]で考えれば十分とするわけです。（これは三角関数の定義域で、逆三角関数から見れば値域になります。）

また、普通は三角関数の１周期分を０を含む範囲で考えて、先ほども触れましたが逆三角関数の値がそこに含まれる事を指して主値と呼ぶ事があります。例えば sinｘ＝０となるｘは０，π、２π、・・・のように無限にあり得るわけですが、主値を使うなら Arcsin０＝０です。
何のことわり書きも無ければ、普通は逆三角関数は主値で考えられています。

逆三角関数として「主値以外の一般の値」も含めている場合は 「arcsinｘ」のように書くと決めている表記法もあります。
ただし逆三角関数と言えば普通は主値を考えるので、どの表記法が正しい間違っているの問題ではありませんが、当サイトでは「断り書きがなければ逆三角関数は主値を考える」ものとして、表記方法は特別な意味をこめずArcsinｘのように書くという事にします。

逆三角関数の値域の制限（主値で考えた時）
  • 逆正弦関数 Arcsinｘ の値域：[－π／２，π／２]
  • 逆正弦関数 Arccosｘの値域：[０，π]
  • 逆正接関数 Arctanｘの値域：[－π／２，π／２]

他方で、定義域では Arcsinｘ と Arccosｘ については [－１，１]であり。

Arctanｘの定義域は （－∞，＋∞）です。

３つの逆三角関数で共通して主値で値を考える場合には、
同じ三角関数の値ｘ（これは変数ではなく関数値）に対するArcsinｘとArccosｘについて
sin(Arcsinｘ)＝cos(Arccosｘ)＝sin(π／２－Arccosｘ)であり、
Arcsinｘ＝π／２－Arccosｘ ⇔ Arcsinｘ＋Arccosｘ＝π／２の関係式が成立します。
ここで主値におけるArccosｘの値域は [０，π]、でArcsinｘの値域が [－π／２，π／２]なので
範囲の整合性はとれているわけです。

主値で値域を考える時に成立する式

主値で考える時には次式が成立します。$$\mathrm{Arcsin}x+\mathrm{Arccos}x=\frac{\pi}{2}$$

初等関数としての逆三角関数の位置付け

逆三角関数は、分類としては実は初等関数に含まれます。
少し妙に思えるかもしれませんが、一応それには理由があります。

初等関数とは、程度の低い関数という意味では無くて数学において基礎となっていて非常に多く使う種類の関数をまとめて呼ぶ総称です。そこに実は逆三角関数も含まれるわけです。（初等関数に対する語は「特殊関数」です。多くは積分や級数で表され、ベータ関数、ガンマ関数、ゼータ関数など多数あります。）

具体的には、次の関数およびその四則演算（平方根なども含む）と逆関数、合成関数を指します。

  • 単項式ｘa（aは実数）
  • 三角関数 sinｘなど
  • 指数関数 eｘなど

さてここで「対数関数」lnｘ＝logeｘを敢えて入れませんでしたが、対数関数も初等関数の１つです。ただし、対数関数は指数関数の逆関数です。（指数関数が対数関数の逆関数であると言っても正しい。）そのため、同じ初等関数の中でそれら２つは対になっているわけです。
【双曲線関数 sinhｘなども初等関数の１つですが、指数関数によって定義されます。】

また、単項式についてもｘaとｘ１／aが互いに逆関数の関係になっています。
例えばｘ≧０におけるｙ＝ｘ２の逆関数はｙ＝ｘ１／２＝\(\sqrt{x}\) です。

「逆数」と「逆関数」の違いに注意すると、逆三角関数での話との関連が見えるでしょうか。
ｙ＝ｘの逆数はｙ＝１／ｘ＝ｘ－１ですが、逆関数は全く同じ形のｙ＝ｘです。ｙ＝ｘ２の逆関数はｘ≧０の範囲でｙ＝ｘ１／２になりますが、それに対してｙ＝ｘ－２＝１／(ｘ２)です。
また逆三角関数の値域の話と同様に、
何の条件もなくｙ＝ｘ２に対してｘについて解くとｘ＝\(\pm\sqrt{y}\) であり、解が２つがあり得るわけですがｘ≧０のような制限があるとプラスの値だけに決まります。

そこで「じゃあ三角関数の逆関数ってどういうものか？」というところにつながるわけです。

指数関数にも単項式にも逆関数を考える事ができて、それではつまり、初等関数という枠組みで見ると三角関数だけ逆関数を敢えて考えない数学的な理由は無くて、むしろ考えておいたほうが整合性が色々ととれる事になります。

ただし、指数関数と対数関数の関係のように逆三角関数にも単独で積極的に活用できる性質があるのかというと、他の初等関数と比べるとそういう面は「やや弱い」と言えそうです。

確かに逆三角関数の性質として「角度が値として分かる」というのはあるのですが、そもそも角度というものが特別ないくつかの値以外は把握も測定もしづらいところがあるから三角比や三角関数を考えているのでもあります。

しかし次に見るように、微分と積分について考えると少なくとも数学上の活用方法は出てきます。

逆三角関数の微分の公式

値域を主値で考えた時の逆三角関数の微分公式を挙げておきます。（ただし、微分そのものが積極的に使われるというよりは、むしろその逆演算である積分のほうでの使い道がやや多いです。）

Arcsinｘの微分などと聞くといかにも面倒くさそうですが、実は三角関数の微分に対して逆関数の微分公式を適用するとすぐに導出できるのです。ｘやｙの変数の扱いにだけ注意すれば意外と難しくないのではないかと思います。

通常の三角関数の微分によって得られる導関数はそれぞれ次のようになります。

  • (ｄ／ｄｘ)sinｘ ＝cosｘ
  • (ｄ／ｄｘ)cosｘ＝－sinｘ
  • (ｄ／ｄｘ)tanｘ ＝１＋tan２ｘ＝１／(cos２ｘ)

これらに対して逆関数の微分公式を使うと、変数の表記方法に注意して３つの逆三角関数の微分公式を導出する事ができます。

逆三角関数の微分公式

逆三角関数の値を主値で考えた時、微分による導関数は次のようになります。
■逆正弦関数 Arcsinｘ の導関数
$$\frac{d}{dx}\mathrm{Arcsin}x=\frac{1}{\sqrt{1-x^2}}$$ ■逆余弦関数 Arccosｘ の導関数
$$\frac{d}{dx}\mathrm{Arccos}x=-\frac{1}{\sqrt{1-x^2}}$$ ■逆正接関数 Arctanｘ の導関数
$$\frac{d}{dx}\mathrm{Arctan}x=\frac{1}{1+x^2}$$ ArcsinｘとArccosｘに関してはｘ≠－１かつｘ≠１のもとで考えます。

Arcsinｘ と Arccosｘ については定義域は [－１，１]ですが
微分を考える時はｘ＝±１を除いて (－１，１)の範囲だけで考えます。
その範囲内では平方根の中身は必ずプラスの値になります。
また、よく見ると導関数が定義できる範囲でArcsinｘ と Arctanｘ の導関数は常にプラスの値で
Arccosｘ の導関数は逆に常にマイナスの値です。
実際 Arcsinｘ と Arctanｘは主値を考える時の値域[－π／２，π／２]で単調増加関数であり、
逆に Arccosｘ は主値を考える時の値域[０，π]において単調減少関数です。

これらの公式は比較的簡単な計算により導出できます。
Arcsinｘ と Arccosｘの導関数が符号だけの違いである理由も導出の過程を見ると分かるでしょう。
計算の注意点としては例えば逆正弦関数ではｙ＝Arcsinｘとした時、sinｙ＝ｘであるので逆関数の微分公式にもそれを当てはめる必要があるといった事です。

$$\frac{d}{dx}\mathrm{Arcsin}x=\frac{1}{\frac{d}{dy}\sin y}=\frac{1}{\cos y}=\frac{1}{\sqrt{1-\sin ^2y}}=\frac{1}{\sqrt{1-x^2}}$$

$$\frac{d}{dx}\mathrm{Arccos}x=\frac{1}{\frac{d}{dy}\cos y}=-\frac{1}{\sin y}=\frac{1}{\sqrt{1-\cos ^2y}}=\frac{1}{\sqrt{1-x^2}}$$

$$\frac{d}{dx}\mathrm{Arctan}x=\frac{1}{\frac{d}{dy}\tan y}=\frac{1}{1+\tan^2y}=\frac{1}{1+x^2}$$

ArcsinｘとArccosｘの微分の途中の計算では sin２ｘ＋cos２ｘ＝１の関係を使っています。
Arctanｘの微分においては、途中計算では微分の公式以外には特に何も使わずに
ｙ＝Arctanｘ から tanｙ＝ｘであるという関係だけを使っています。

この導出の過程でArcsinｘの導関数については cosｙ＝\(+\sqrt{1-\sin^2y}\)のように考えています。（マイナスではなくプラスの値としています。）これはArcsinｘを主値で考えており、
値域（三角関数から見れば定義域）を [－π／２，π／２]として考えているためです。
その範囲ではcosｙ≧０となります。（ただしここではxosｙ＝０となる端点を除いています。）
他方でArccosｘについては値域を [０，π]として考えているのでその範囲ではsinｙ≧０です。
（先ほどと同じく実質はsinｙ＞０で考えます。）
ゆえにsinｙ＝\(+\sqrt{1-\cos^2y}\)としています。

逆関数の微分公式

逆三角関数に限らず、逆関数一般について次の関係式が成立します。 $$\frac{dy}{dx}=\frac{1}{\Large{\frac{dx}{dy}}}$$ この式を実際の計算で使う時にはｙとｘの関係について注意が必要です。
ｙ＝Arcsinｘの時にはｘ＝sinｙですから、ｙをｘで微分した時に逆関数の微分公式での分母は「ｘ＝sinｙをｙで微分した導関数」つまり cosｙが入ります。

逆三角関数の積分の公式

さて、微分が分かれば積分のほうも分かる事になりますが、逆三角関数の導関数は意外にも「式としては三角関数が全然関係ない」という形になっています。ですので図形問題や三角関数を考えているわけではなくても積分に使える場合があるのです。

原始関数が逆三角関数で表される不定積分

平方根の中身が０より大きくなる定義域において、次の積分公式が成立します。 $$\int \frac{1}{\sqrt{1-x^2}}dx=\mathrm{Arcsin}x+C$$ $$\int -\frac{1}{\sqrt{1-x^2}}dx=\mathrm{Arccos}x+C$$ $$\int \frac{1}{1+x^2}dx=\mathrm{Arctan}x+C$$ $$\int \sqrt{a^2-x^2}dx=\frac{1}{2}\left(x\sqrt{a^2-x^2}+a^2\mathrm{Arcsin}\frac{x}{a}\right)+C$$ Cは任意の実数定数です。
４番目の式については部分積分の公式を使って導出するもので、実用性は別問題として
「逆三角関数を使って原始関数を表せる」という例です。（置換積分でも計算は可能。）

このような形の関数の積分を考える時には置換積分や部分積分を考える必要はなくて、そのまま逆三角関数を当てはめる事ができます。

これらの積分の式について原始関数が Arcsinｘと Arccosｘになる２式を特に見比べると、
被積分関数が符号だけの違いとなっています。
ここで「符号が違うだけで積分の結果が変わるものか？」と妙に思えるかもしれませんが、
Arcsinｘ＝－Arccosｘ＋π／２の関係があるので、Arcsinｘと Arccosｘは互いに変換が可能です。
不定積分においてはπ／２は任意定数に含める事ができるので、Arcsinｘのほうの不定積分の式の両辺に－１を乗じた場合には式としてはArccosｘのほうの不定積分の式に変える事はできます。

例１：逆正接関数のマクローリン展開と角度計算

逆三角関数はある三角関数の値から角度を逆算できる関数ではありますが、関数としての実態が分からないと結局特別な値以外は簡単には計算できない事になってしまいます。

「それでも別に支障ない」と言ってしまえばそれまでですが一応、マクローリン展開（ｘ＝０におけるテイラー展開）を使えば逆三角関数の近似値をｘから直接計算する事は可能です。

ただし、計算しやすい形になっているのは逆正接関数Arctanｘのマクローリン展開ですので、
それについて説明をします。

展開式（無限級数展開）の内容

Arctanｘのマクローリン展開は、意外かもしれませんが正弦関数や余弦関数のマクローリン展開に形は似ていて、式自体はそれほど複雑ではありません。

逆正接関数Arctanｘのマクローリン展開

逆正接関数Arctanｘはマクローリン展開可能（ｘ＝０でテイラー展開可能）であり、
|ｘ|＜１において次式で表す事ができます。 $$\mathrm{Arctan}x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\frac{x^9}{9}-\frac{x^{11}}{11}+\cdots$$ （ｘ＝１においても一応この式は収束します。）

この式で、てきとうにｘ＝１／５などどしてみると、
Arctanｘ＝１／５－１／(５３・３)＋１／(５５・５)－・・・
４項目以降はほぼ０であると考えると、
Arctanｘ＝１／５－１／３７５＋１／１５６２５－・・・≒０．１９７４≒０．０６２８π
これは度数法で言うとおおよそですが１８０×０．０６３５８≒１１．３°です。

このような数値の計算は、計算ソフトや関数電卓で直接的に計算できるならそれを使えばよいという話でもあるのですが、一応このように計算もできるという事です。（また、ソフト等を使うにしても逆三角関数によって「角度」を計算できる事は理系の人であれば一応知っておいてもよいのではないかと思います。）参考までにおおよその値の例をいくつか挙げておきます。

tanｘArctanｘ（＝弧度法での角度）\(a\pi\)の形で表す時度数法での角度 [ °]
0.990.7800.248\(\pi\)44.71
0.90.7330.233\(\pi\)41.99
0.80.6740.215\(\pi\)38.66
0.70.6110.194\(\pi\)34.99
0.50.4640.148\(\pi\)26.57
0.30.2910.093\(\pi\)16.70
0.10.09970.032\(\pi\)5.711

尚、tan(π／４)＝１ですので Arctan１＝π／４≒0.786[rad]で、度数法では４５°です。

また、０に近い角度であればArctanｘ≒ｘとも言えます。
ただし同じくマクローリン展開からsinｘ≒ｘも同様に分かるので、０に近い角度であれば通常の正弦関数で考えたほうがむしろ早い事にはなります。

参考までに、Arcsinｘのマクローリン展開は |ｘ|＜１の範囲で次式のようになります。
これはArcsinｘの導関数を２項定理によって展開する事で得られますが、Arctanｘと比較して結構面倒な形だと言えそうです。$$\mathrm{Arcsin}x=x+\sum_{n=1}^{\infty}\left(\frac{1\cdot3\cdot5\cdots(2n-1)}{2\cdot4\cdot8\cdots(2n)}\frac{\large{x^{2n+1}}}{2n+1}\right)$$

Arctanｘのマクローリン展開の導出

この式は、前述の微分公式を使って普通にマクローリン展開を考えて導出しようとすると、実は結構大変です。というのも、１階と２階の微分はよいとしても、３階、４階・・・と高階微分を計算していくと形が複雑になるためです。

しかし実は、１階の微分後に幾何級数展開（等比級数による展開）する事でArctanｘのマクローリン展開は導出できるのです。また、それによって各高階導関数のｘ＝０における微分係数も判明する事になります。（これは、そのように考えてよいという定理があります。）

まず(ｄ／ｄｘ)Arctanｘ＝１／(１＋ｘ２)であるわけですが、
|ｘ|＜１であればこれは幾何級数が収束する値として考える事ができて、
具体的には次のようになります。
１－ｘ２＋ｘ４－ｘ６＋・・・＝１＋(－ｘ２)＋(－ｘ２)２＋(－ｘ２)３＋(－ｘ２)４＋・・・
これは、「公比が－ｘ２である等比級数」「公比が－ｘ２である等比数列の項数を無限大にした極限」と言っても同じです。

よって、|ｘ|＜１の範囲では(ｄ／ｄｘ)Arctanｘ＝１－ｘ２＋ｘ４－ｘ６＋・・・

そこで、この関数については項別積分が可能なので（※無限級数に対して項別積分が可能であるのは「収束円の内部においてだけ」という条件が必要なので注意）、|ｘ|＜１のもとで各項を積分すると次のようになります。積分変数をｔとして、０からｘまでの定積分という形にします。

$$\int_0^x\left(\frac{d}{dt}\mathrm{Arctan}t\right)dt=\int_0^x\left(1-t^2+t^4-t^6+\cdots\right)dt$$

$$\mathrm{Arctan}0=0に注意すると\int_0^x\left(\frac{d}{dt}\mathrm{Arctan}t\right)dt=\mathrm{Arctan}xであるので$$

$$\mathrm{Arctan}x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots$$

このようにして得られた級数は、実はマクローリン展開に等しくなります。
（無条件にではなく、ここでの場合はそうなります。）

無限級数に対して項別積分が可能であるかの数学的な問題を避けたい場合には、有限の和に対して積分をする方法もここでは適用できます。
S＝１＋(－ｘ２)＋(－ｘ２)２＋(－ｘ２)３＋(－ｘ２)４＋・・・＋(－ｘ２)ｎ　
両辺に－ｘ２を乗じると次式です。
－ｘ２Ｓ＝(－ｘ２)＋(－ｘ２)２＋(－ｘ２)３＋(－ｘ２)４＋(－ｘ２)5＋・・・＋(－ｘ２)ｎ＋(－ｘ２)ｎ＋１
両辺について１式目から２式目を引くと次式です。
(１＋ｘ２)Ｓ＝１－(－ｘ２)ｎ＋１
⇔Ｓ＝１／(１＋ｘ２)－(－ｘ２)ｎ＋１／(１＋ｘ２)
【そのため、|ｘ|＜１であればｎ→∞でＳ→１／(１＋ｘ２)】
ここで、敢えて極限を考えずに式を整理すると有限のｎに対して
Ｓ＋(－ｘ２)ｎ＋１／(１＋ｘ２)＝１／(１＋ｘ２)です。
そしてSに対して元の式を代入すると、
１／(１＋ｘ２)＝１＋(－ｘ２)＋(－ｘ２)２＋(－ｘ２)３＋・・・＋(－ｘ２)ｎ＋(－ｘ２)ｎ＋１／(１＋ｘ２)
これは有限の項の和ですので、項別積分は可能です。
そこで項別積分を実施すると、有限の範囲でのマクローリン公式（ｘ＝０におけるテイラー公式）を作れます。その後で、積分型の剰余項の収束について考える必要があります。（結果は剰余項はｎ→∞で０に収束します。）

例２：ライプニッツ級数の導出

ライプニッツ級数とは、数学的に成立するという事以上の意味はそれほど無いとも言われますが円周率を無限級数で表す式です。さらに、各項は簡単な有理数で表されているという「不思議な式」です。

ライプニッツ級数を導出する方法は複数ありますが、実は逆正接関数を使う方法がその１つです。

ライプニッツ級数

次の無限級数は収束し、値は円周率の１／４倍になります。
$$1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}+\cdots=\frac{\pi}{4}$$ これは「近似値」とは少し違うもので、「π／４を極限値として持つ」という意味において成立する「等式」になります。

ところで、この式に非常に似た形の式をこの記事内で先ほど考察していて、
それが逆正接関数 Arctanｘのマクローリン展開です。実の所、Arctanｘのマクローリン展開で
「ｘ＝１と置いたもの」はライプニッツ級数に他なりません。

それは偶然ではなく、きちんと証明できます。ただし Arctanｘのマクローリン展開を幾何級数から導出する時には |ｘ|＜１の条件をつけていましたから、単純に「ｘ＝１を代入」するのは少し危ない操作であると言えます。もしかしたら、ｘ＝１では無限級数は無限大に発散するかもしれないからです。

しかし実際は、ｘ→１とした時にもｘ－ｘ３／３＋ｘ５／５－ｘ７／７＋・・・は収束します。

ライプニッツ級数が収束する事自体は実は比較的簡単な考察により分かる事で、ｎ項目までの和Ｓｎについて奇数番目と偶数番目を分けて考える事で証明できます。

S２ｎ－１に対してＳ２ｎはマイナスの項が加わって少し減りますが、S２ｎ＋１でまた少し増えます。しかし項の絶対値自体は減り続けるため、S２ｎ－１の値までは戻りません。
よってS２ｎ－１＞Ｓ２ｎ＋１です。
すなわち奇数番目までの和だけに着目すると｛S２ｎ－１｝は単調減少数列となっています。
逆に遇数番目までの和Ｓ２ｎに着目すると｛Ｓ２ｎ｝は単調増加数列となります。
さらに、プラスとマイナスが交互に現れるので必ずS２ｎ－１＞Ｓ２ｎでもある事から
任意の自然数ｎに対してS２ｎ＜S２ｎ－１＜S１＝１により｛Ｓ２ｎ｝は上に有界であり、
S２ｎ－１＞Ｓ２ｎ＞Ｓ２＝２／３であり、｛Ｓ２ｎ－１｝は下に有界です。
つまり両者ともに有界な単調数列なので｛Ｓ２ｎ－１｝と｛Ｓ２ｎ｝はそれぞれ収束し、
さらにＳ２ｎ－Ｓ２ｎ－１を考えてみると各項の絶対値は０に近づいて行くので
ｎ→∞でＳ２ｎ－Ｓ２ｎ－１→０です。
つまりｎ→∞で｛Ｓ２ｎ－１｝と｛Ｓ２ｎ｝は同じ値に収束します。
すなわち、級数全体も収束する事になります。（ただし、極限値はまだ不明です。）
この事は実はライプニッツ級数に限らず、プラスマイナスが交互に現れる交代級数について「項の絶対値が単調減少でｎ→∞で０に収束する」という条件があれば級数も収束するという定理があります。（ライプニッツの定理と呼ばれる事があります。）

Arctanｘ自体はｘ＝１以上でも全実数において値を持ちます。Arctan１＝π／４です。
（π／４は度数法で言えば４５°の角度です。）

そこで|a| ＜１に対してπ／４－（a－a３／３＋a５／５－a７／７＋・・・）を考えます。
Arctan１＝π／４であり、
|a| ＜１に対してはマクローリン展開により、
Arctan a＝a－a３／３＋a５／５－a７／７＋・・・です。
よって、π／４－（a－a３／３＋a５／５－a７／７＋・・・）＝Arctan１－Arctan a となります。

ここでa→１の極限を考えますが、
Arctanｘは連続関数なのでa→１の極限ではArctan a→Arctan１です。
それは当然と言えば当然の関係ではあるのですが、
それによってマクローリン展開の式もArctan１に収束する事が分かります。
つまりはa→１で a－a３／３＋a５／５－a７／７＋・・・→π／４となるわけです。

「Arctanｘが連続関数である事」の部分を少し詳しく見ると次のようになります。
まずtanｘが連続関数であり、「狭義単調増加（ｘ＜ｗに対してf(ｘ)＜ｆ(ｗ)となる）または狭義単調減少であればその逆関数もまた連続であり、ｘ＝１においても連続」となります。
今、ｆ(ｘ)＝Arctanｘとするとｘ＝１で連続であるから
「１を含むある開区間Ｕがあって、任意の実数ε＞０に対してＵの区間の長さを十分小さくすれば、Ｕに含まれる任意の実数ｘに対して |ｆ(１)－ｆ(ｘ)|＜εとなるようにできる」
という事になります。
つまり先ほどの|a| ＜１であるaについて任意の実数ε＞０に対して
|ｆ(１)－ｆ(ｘ)|＜εとなる「１を含む開区間U」に含まれているものを選べば、
任意の実数ε＞０に対して|ｆ(１)－ｆ(a)|
＝|Arctan１－Arctan a|＝ |π／４－（a－a３／３＋a５／５－a７／７＋・・・）|＜ ε
よって、a→１の極限では
a－a３／３＋a５／５－a７／７＋・・・→ π／４という事になります。

さてここで、「aを１に置き換えて１－１／３＋１／５－１／７＋・・・＝π／４」としても大体合っているのですが、より正確にやるのであればここでは概略だけに留めますが次の定理を使います。おそらく聞き慣れないかもしれませんが、連続性定理とかアーベルの連続性定理などと呼ばれます。

連続性定理

$$(-\rho,\rho)で収束する\sum_{n=0}^{\infty}a_nx^nがある時$$ $$\sum_{n=0}^{\infty}a_n\rho^nも収束する\Rightarrow\lim_{x\to{\rho -0}}\sum_{n=0}^{\infty}a_nx^n=\sum_{n=0}^{\infty}a_n\rho^n$$ ρ（ ＞０）は「収束半径」、開区間（－ρ，ρ）は「収束円」とも言います。
極限「ｘ→ρ－０」は「左極限」（もしくは「左側極限」）を表し、
「ρよりも小さい値として近づく」という意味を持ちます。

この定理は一体何を言っているのかというと、ここでの話で具体的に言うと
まず|ｘ|＜１でマクローリン展開により
Arctanｘ＝ｘ－ｘ３／３＋ｘ５／５－ｘ７／７＋・・・となるのでこの級数は収束しています。
次にｘ＝１の時に相当する式である１－１／３＋１／５－１／７＋・・・は
収束する事が個別の考察で分かっている状況です。しかし極限値は不明です。
そこで連続性定理によれば
１－１／３＋１／５－１／７＋・・・の極限値は
ｘ－ｘ３／３＋ｘ５／５－ｘ７／７＋・・・
の左側極限ｘ→１－０の極限値に等しいという事になります。
そして、ｘ－ｘ３／３＋ｘ５／５－ｘ７／７＋・・・のｘ→１－０の時の極限値は
Arctanｘの連続性によりArctan１＝π／４という事が分かっているので、
１－１／３＋１／５－１／７＋・・・＝π／４という結果を得るという流れです。 $$|x|<1 で\mathrm{Arctan}x=x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdotsであり、収束する。$$ $$x=1に相当する1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}-\frac{1}{11}+\cdotsは収束する事が示されている。$$ $$今、\mathrm{Arctan}xの連続性により\lim_{x\to{1-0}}\left(x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots\right)=\mathrm{Arctan}1=\frac{\pi}{4}$$ $$連続性定理により1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots=\lim_{x\to{1-0}}\left(x-\frac{x^3}{3}+\frac{x^5}{5}-\frac{x^7}{7}+\cdots\right)$$ $$=\mathrm{Arctan}1=\frac{\pi}{4}$$

ライプニッツ級数を導出する他の方法としては、４分円（円の１／４）の面積を積分で計算する方法があります。ただし通常のｘ軸方向の積分ではなく、ｙ軸を利用した少し工夫が凝らされた計算になります。実はその場合でもArctanｘのマクローリン展開を考えた時と同様に幾何級数展開による計算を行います。

例３：マチンの公式による円周率の表現

再び数学的な話ではありますが、円周率を表す式は実は１つではなくたくさんあります。ライプニッツ級数は「その１つ」であり、不思議な式ではありますが「収束の速さが遅い」事でも実は知られています。収束の速さが遅いという事は、直接計算してもなかなか「３．１４・・・」が出てこない事を意味します。

他方で収束が速い円周率の公式も知られていて、その１つがマチンの公式という逆三角関数で表されるものです。ここでは通常の三角関数における正接の加法定理を使った証明方法を簡単に説明します。

マチンの公式

次の式で円周率を表せるという事が知られています。 $$4\mathrm{Arctan}\left(\frac{1}{5}\right)-\mathrm{Arctan}\left(\frac{1}{239}\right)=\frac{\pi}{4}$$ これもライプニッツ級数同様に「等式」として成立する関係式であり、
さらにこの式に関しては極限の計算などは特に必要としません。

ここではこの奇怪な式が「確かにπ／４に一致する」事の確認を優先する形で証明を述べます。

最初に結論を言うと、マチンの公式の左辺は正接関数に対する「角度」であり、その角度を持つ正接の値が１になる事で「角度＝π／４」という事が言えます。

$$示すべき式：\tan\left(4\mathrm{Arctan}\left(\frac{1}{5}\right)-\mathrm{Arctan}\left(\frac{1}{239}\right)\right)=1$$

普通の角度で考えるなら tan(４θ１＋θ２)＝１となる事を証明する事になります。

加法定理を使うと、tan(４θ１＋θ２)＝｛tan(４θ１)－tanθ２｝／[１＋{tan(４θ１)}(tanθ２)}ここで、少し面倒ですが４θ１に対して倍角の公式（加法定理でも同じ）を２回使います。
tanθ１＝１／５とすると上手く行くのでその値を代入します。

$$\tan(2\theta_1)=\frac{2\tan\theta_1}{1-\tan^2\theta_1}=\frac{2}{5}\cdot\frac{25}{24}=\frac{5}{12}$$

再度、倍角の公式を使います。具体的な数値を入れます。

$$\tan(4\theta_1)=\frac{2\cdot\frac{5}{12}}{1-\left(\frac{5}{12}\right)}=\frac{5}{6}\cdot\frac{144}{119}=\frac{120}{119}$$

これを、最初のtan(４θ１＋θ２)＝｛tan(４θ１)－tanθ２｝／[１＋{tan(４θ１)}(tanθ２)}に代入します。
θ２の値は結論から言えば１／２３９ですが、ちょっとここでは「確かにその値にすればよい」という事を式を解く形で見てみる事にしましょう。
tanθ２＝Xとおきます。

$$\frac{\frac{120}{119}-X}{1+X\frac{120}{119}}=1\Leftrightarrow\frac{120}{119}-X=1+X\frac{120}{119}$$

$$\Leftrightarrow X\frac{239}{119}=\frac{1}{119}\Leftrightarrow X=\frac{1}{239}$$

これを見ると、「２３９」という謎の半端な数字が１２０＋１１９である事が分かります。以上から、結論が完全に分かっている前提での証明でしたが確かにマチンの公式が成立している事が分かります。

$$\frac{\frac{120}{119}-\frac{1}{239}}{1+\frac{1}{239}\frac{120}{119}}=\frac{28680-119}{28441+120}=\frac{28561}{28561}=1$$

$$よって、\tan\left(4\mathrm{Arctan}\left(\frac{1}{5}\right)-\mathrm{Arctan}\left(\frac{1}{239}\right)\right)=1なので$$

$$4\mathrm{Arctan}\left(\frac{1}{5}\right)-\mathrm{Arctan}\left(\frac{1}{239}\right)=\frac{\pi}{4}$$

Arctanｘのマクローリン展開からマチンの公式の左辺を計算すると、
おおよそ４×０．１９７４－１／２３９≒０．７８５≒π／４となり、確かに公式の内容が成立している事を見れます。【Arctan(１／２３９)≒１／２３９としました。】
しかし上式を見れば分かるようにマチンの公式自体は近似式ではなく「等式」であり、しかも極限を含んでいない事が特徴です。

実は円周率を表す式としては「マチン型」というタイプのものが複数あって、比較的有名なものだとオイラーによるものとガウスによるものがあります。いずれもπ／４を逆正接関数の具体的な値の和や差で表す公式です。

例４：有理関数の積分に関する定理

これもまた数学の理論的な話ではありますが、間接的には応用にも関わる問題として
「有理関数（多項式の分数で表される関数）の一般的な積分は原始関数としてどのように表せるか」
というものがあります。

実はそれは初等関数のみで表す事ができ、しかも有理関数、対数関数、逆正接関数とそれらの合成関数さえあれば（理論上は）足りる」という結果を述べる定理があります。
意外かもしれませんが「逆正接関数Arctanｘ」が必要な関数として入っているわけです。

有理関数の積分

２つの多項式P(ｘ)とＱ(ｘ)がある時、P(ｘ)／Ｑ(ｘ)で表される有理関数の不定積分は理論上、次の関数によって表す事ができます。

  • （別の）有理関数V(ｘ)／W(ｘ)
  • 対数関数（底は e）
  • 逆正接関数 Arctanｘ
  • これら３つの合成関数
また、置換積分を行う事で三角関数で構成される有理関数も。S(ｔ)／T(ｔ)の形の積分にできるので有限回の操作で原始関数を見つける事が理論上は可能です。

ここで「理論上」という語を付したのは「数学的に可能であるという事」と「それが便利であるか・使いやすいか」という事は別の問題である事も多いからです。

しかし理論上の話ではあっても、「原始関数を探す形で積分はどこまで計算できるのか？」という疑問に対して「三角関数の使用も含めて有理関数の範囲では、原始関数は初等関数の組み合わせで必ず導出する事が一応可能である」という一定の答えを述べている定理でもあります。

有理関数とは

有理関数とは例えば次のようなものです。 $$\frac{P(x)}{Q(x)}=\frac{p_0+p_1x+p_2x^2+p_3x^3}{q_0+q_1x+q_2x^2+q_3x^3+q_4x^4}$$ $$具体例：\hspace{5pt}\frac{P(x)}{Q(x)}=\frac{2-x+3x^2+x^3}{1+x+2x^3-x^4}$$ 三角関数の有理関数の例 $$\frac{1-\tan^2x}{1+\tan^2 x}$$

定理の証明の概略を記すと、まず分子の次数のほうが分母よりも大きい場合には多項式の割り算をして、分母の次数のほうが大きい状態にします。

次に分母の多項式を因数分解して、そこから部分分数展開をする事を考えます。

「因数分解と言うができないような多項式だったらどうするのか」と思われるかもしれませんが、実は任意の多項式は何かしらの複素数（実数を含めて）を用いて理論上は因数分解できる事が知られています。それはいわゆる代数学の基本定理による帰結です。

計算をすると、任意の多項式は次の３つの項に分類して分ける事ができます。

  • 分母が定数である（１を含めて）多項式
  • 分母が１次式のベキ乗で分子は定数である項
  • 分母が２次式のベキ乗で分子は１次式である項

因数分解をした時に実数以外の複素数が含まれている場合には共役を上手く使って虚数単位が式に現れないように工夫します。分母が２次式のベキ乗の項にはその意味があります。

さてその段階に至ると原始関数を探す形で積分ができます。この時に、使用する初等関数の種類は理論上３つであるという事が言えるのです。

  • 単項式と多項式および有理関数：
    分母に分母に定数以外が含まれない多項式および１／{(ｘ－a)ｎ}【ｎ≧２】、
    分母が２次の項に由来するｘ／{(ｘ２＋１)ｎ}【ｎ≧２】
  • 対数関数：１／(ｘ－a)および分母が２次の項に由来するｘ／(１＋ｘ２)の項
  • 逆正接関数：２次の項に由来する１／(１＋ｘ２)の項

こうして見ると積分をする時に問題が生じるのが「分母の式」であって、１／(１＋ｘ２)の項を処理する時にどうしても必要なのが逆正接関数という事になります。
その項の不定積分は前述のように Arctanｘ＋Ｃです。

複素数の極形式（極表示）と偏角

恭平

複素数の極形式（あるいは「極表示」）の定義と計算方法を説明します。これは三角関数と複素数の密接な関係を表すもので、複素数を平面図形的に扱える根拠ともなっています。

目次：

  1. 極形式とは？三角関数と複素数の密接な関係
  2. 複素数の乗法と除法、ド・モアブルの定理

考え方の基本は、複素数の定義と、ｘｙ平面上の極座標の考え方を組み合わせるというものになります。それによって、複素数の乗法と除法（掛け算と割り算）には、独特の性質を持つ事が分かるようになります。

BGM:MUSMUS　CV:CeVIOさとうささら

複素数の極形式とは？三角関数と複素数の密接な関係

複素数を三角関数で表現したものを複素数の極形式あるいは極表示と呼びます。じつはこれは、複素関数論や物理学等で、複素数を使う場合に本質的に重要になるのです。

複素数を次のように、三角関数を使った形で表したものを複素数の極形式と言います。

複素数の「極形式」

$$z=a+biの「極形式」：z=|z|(\cos \theta + i\sin \theta)$$ $$\cos \theta=\frac{a}{|z|}=\frac{a}{\sqrt{a^2+b^2}}\hspace{15pt}\sin \theta=\frac{b}{|z|}=\frac{b}{\sqrt{a^2+b^2}}$$

$$複素数の絶対値 |z| を r で表して、z=r(\cos \theta + i\sin \theta)の形式でもよく書かれます。$$

式だけ見ると唐突で複雑に見えるかもしれませんが、
じつはこれは図形的に理解してから式の意味を整理すると分かりやすいのです。

複素数の実部を直交座標のｘｙ平面のｘ座標とみなし、
複素数の虚部（の実数係数部分）をｙ座標とみなす考え方があります。
そのように考えた仮想的な平面を複素平面と言い、
その時のｘ軸に相当する軸を「実軸」、ｙ軸に相当する軸を「虚軸」と呼んだりします。
そのように考えると複素数を図形的に捉える事ができるようになり、考察をさらに進めると複素数の極形式の考え方が出てくるのです。

複素平面と実軸・虚軸
複素数の実部をx座標、虚部の係数をｙ座標にプロットします。このような「複素平面」において、複素数の絶対値は「原点から複素数を表す点までの距離」という図形的意味を持ちます。

複素平面において、まず「絶対値を原点から複素数までの距離」と考えます。すると、通常のｘｙ平面における極座標の考え方を使えば、複素数の実部と虚部を三角関数を使って表せるはず・・・と考察したものが、上記の複素数の極形式の形なのです。

尚、絶対値を平方根で敢えて書いている部分 \(\cos \theta=\Large{\frac{a}{|z|}=\frac{a}{\sqrt{a^2+b^2}}}\)は、
図で表している部分を式で書いた表現になります。
単純に、直角三角形の１つの辺を斜辺で割った値として余弦や正弦を考えています。
（a や b はマイナスの値もとるので、角度は三角関数に対する一般角を考えている事になります。）

三角関数とみなしている項の部分\(\Large{\frac{a}{|z|}=\frac{a}{\sqrt{a^2+b^2}}}\)と\(\Large{\frac{b}{|z|}=\frac{b}{\sqrt{a^2+b^2}}}\)は、
値が必ず -1 以上 +1 以下です。（２乗してみるとすぐに分かります。）
さらに、これらを２乗して互いを加え合わせたものは１に等しくなります。

$$\left(\frac{a}{|z|}\right)^2+\left(\frac{b}{|z|}\right)^2=\left(\frac{a}{\sqrt{a^2+b^2}}\right)^2+\left(\frac{b}{\sqrt{a^2+b^2}}\right)^2$$

$$=\frac{a^2}{a^2+b^2}+\frac{b^2}{a^2+b^2}=\frac{a^2+b^2}{a^2+b^2}=1$$

これらの事が三角関数の定義と調和しており、
そのために、三角関数としてみなせるという事なのです。

この時に、三角関数として表すからには「対応する角度が必ず存在する」はずですが、
それは実際に考える事ができるのです。しかもその仮想的な角度は、とりあえず数学上の辻褄合わせで考えておくというだけでなく、複素数の計算理論において重要な量なのです。

複素数に対して新たに導入した三角関数の角度部分として、新たに設定した実数 θ を、
その複素数の偏角と言います。複素数 z に対して arg z と表記する事もあります。
（英語では偏角の事を argument と言います。）

このように、複素数を「複素平面」に図示して考える時もあります。
この時、複素数同士の積は「複素平面上の『回転』」を表します。
複素数の極形式は、複素数の指数関数表示とも直接的に関わります。

複素数の乗法と除法、ド・モアブルの定理

複素数を極形式で表した時に成立する重要公式があり、それは
「２つの複素数の積は、『絶対値の積』と『偏角の和』で計算できる」というものです。

複素数の乗法・積に関して成立する公式

$$u=|u|(\cos \theta + i\sin \theta),\hspace{10pt}w=|w|(\cos \phi + i\sin \phi)のとき、$$ $$uw=|u||w|\{\cos (\theta+\phi)+i\sin (\theta+\phi)\}$$

この公式において絶対値が１で u ＝ w の時、すなわち絶対値が１の複素数のベキ乗（「ｎ乗」の事）を考えた場合の式は特にド・モアブルの定理と呼ばれる事が多いです。

$$ド・モアブルの定理：(\cos\theta+i\sin)^n=\cos(n\theta)+i\sin(n\theta)$$

他方で除法（割り算）の場合には、絶対値の部分を割り算し、割るほうの複素数の偏角にマイナス符号をつけて掛け算します。つまり、除法の場合は偏角部分を引き算する計算になるのです。

複素数の除法・商に関して成立する公式

$$u=|u|(\cos \theta + i\sin \theta),\hspace{10pt}w=|w|(\cos \phi + i\sin \phi)のとき、$$ $$\frac{u}{w}=\frac{|u|}{|w|}\{\cos (\theta-\phi)+i\sin (\theta-\phi)\}$$

この除法に関するほうの公式は、乗法の場合において片方の偏角 φ の符号を入れ替えて －φ に置き換えたものとみなす事もできます。
マイナスの角度というのは、
「平面上で通常の角度の向き（反時計回り方向）に対して『逆の方向（時計回り方向）』」に向けての角度と考える事ができますから、複素平面上の図形的な捉え方においても乗法の場合の公式で統一的に捉える事が可能です。

除法のほうの公式を考えてみると、ド・モアブルの定理においてべき乗の指数であるｎは自然数だけではなく、マイナスの整数であってもよい事が分かります。
実数の１は「絶対値が１で偏角が０の複素数」と同じものである事に注意します。

$$例えば、(\cos \theta + i\sin \theta)^{-2}=\frac{1}{(\cos \theta + i\sin \theta)^2}=\frac{1}{\cos(2\theta) + i\sin(2\theta)}$$

$$=\cos (0-2\theta)+i\sin (0-2\theta)=\cos (-2\theta)+i\sin (-2\theta)$$

※さらに考察すると、任意の実数 ｘ に対して (cos Θ + i sinΘ)x＝cos (xΘ) + i sin(xΘ) です。

公式の証明

複素数の乗法および除法、ド・モアブルの定理の成立根拠は三角関数の加法定理です。

まず、極形式で表した２つの複素数の積をそのまま計算してみましょう。
すると、実部には余弦に関する加法定理、虚部には正弦に関する加法定理の形が現れるので、加法定理によって変形するとそれがそのまま公式の証明になるのです。

$$uw=|u|(\cos \theta + i\sin \theta)|w|(\cos \phi + i\sin \phi)$$

$$=|u||w|\{ \cos \theta \cos \phi – \sin \theta \sin \phi +i(\sin \phi \cos \theta + \sin \theta \cos \phi )\}$$

$$=|u||w|\{\cos (\theta+\phi)+i\sin (\theta+\phi)\}【証明終り】$$

割り算のほうの公式は、偏角に関しては前述の考え方と同じで片方の符号を入れ替えて、
絶対値部分については |w|＝１／|w| の場合を考えればよいことになります。

あるいは、分母の複素数の共役複素数を分母と分子に掛けて直接証明してもよく、
偏角が θ である複素数の共役複素数の偏角は -θ になりますから、掛け算のほうの公式を使えばよい事になります。

$$乗法の公式で\phiを-\phiに置き換えてもいいし、次のようにしても結果は同じです。$$

$$\frac{u}{w}=\frac{u\overline{w}}{w\overline{w}}=\frac{|u||w|(\cos \theta + i\sin \theta)(\cos \phi – i\sin \phi)}{|w|^2}=\frac{|u|}{|w|}\{\cos (\theta-\phi)+i\sin (\theta-\phi)\}$$

さらなる考察

この極形式の観点から言うと、虚数単位 i は

$$i = \cos \frac{\pi}{2}+i\sin \frac{\pi}{2}$$

とも書ける事は重要です。
複素数の乗法に関する公式とも合わせて考えると、ある複素数に対して虚数単位 i を掛ける操作は、
「複素平面上では『９０°回転』を意味する」という事が分かります。
物理学や一部の工学では、その分だけ「『位相』を進める」といった表現がされる事もあります。

式で書くと次のようになります。

$$i(\cos\theta+i\sin\theta)=\left(\cos \frac{\pi}{2}+i\sin \frac{\pi}{2}\right)(\cos\theta+i\sin\theta)=\cos\left(\frac{\pi}{2}+\theta\right)+i\sin\left(\frac{\pi}{2}+\theta\right)$$

公式の証明の箇所でも触れましたが、
ある複素数の共役複素数は、偏角の符号を入れ替えたものになります。
その事は図形的に見て確認する事もできますが、
虚部の符号を入れ替える事と、cos(－Θ)＝cos および sin(－Θ)＝－sinΘ の関係から見る事もできます。

$$z=\cos\theta +i\sin\thetaに対して、\overline{z}=\cos\theta -i\sin\theta=\cos(-\theta) +i\sin(-\theta)$$

また、極形式で書いた場合でも「ある複素数と共役複素数の積は、絶対値の２乗になる」という事が確かに成立する事が分かります。ある複素数とその共役複素数は、絶対値は同じである事に注意すると次のような計算になります。

$$z\overline{z}=|z|(\cos\theta+i\sin\theta)\cdot|z|\{\cos(-\theta)+i\sin(-\theta)\}$$

$$=|z|^2\{\cos(\theta-\theta)+i\sin(\theta-\theta)\}=|z|^2(\cos 0+i\sin 0)=|z|^2$$

偏角と回転・反転
虚数単位 i を２乗すると－１になるという計算や、虚部の符号を入れ替えた共役複素数についても、極形式の偏角の観点から複素平面上での図形的に解釈が可能です。

さらに、複素数の極形式を表す別の表記方法として複素数の「指数関数表示」というものがあります。これは「オイラーの式」と呼ばれる事もあります。

$$複素数の指数関数表示：e^{ix}=\cos x +i\sin x$$

e は自然対数の底（ネイピア定数）です。このような複素数が混じった指数関数においても、微積分を含めて通常の指数関数と同様の計算が成立します。複素数の乗法と除法の公式を考えると、指数関数の極形式における乗法や除法の計算と実は調和しています。

例えば指数関数の計算規則に従うと複素数の積は次のようになります。

$$e^{ix}e^{iy}=e^{i(x+y)}$$

これをよく見ると、複素数の極形式における乗法の計算と調和しているのです。

$$(\cos x + i\sin x)(\cos y + i\sin y)=\cos (x+y)+i\sin (x+y) $$

参考：複素数に関するサイト内記事

極座標と球面座標【考え方と変換方法】

恭平

座標変換のうち、理論面でも応用面でも良く使われる極座標と、その3次元版である球面座標について述べます。（※３次元の球面座標の事も極座標と呼ぶ事もあります。）
また合わせて、時々使われる円柱座標についても述べます。

目次：

  1. 基本の考え方：三角関数を使う
  2. 変換方法：極座標
  3. 球面座標
  4. 円柱座標

極座標（polar coordinates）の「極」とは英語で言うと pole 、
北極とか南極で使う意味での「極」（「一方の果て」「端、両端」）になります。
尚、球面座標は英語だと spherical polar coordinates です。

関連事項のリンク（サイト内）

基本の考え方：三角関数を使う

極座標の発想自体は簡単で、
「平面座標のある点と原点とを結ぶと、必ず『長さと角度（ｘ軸から測った角度）』で表せるはず」
という事なのです。

例えば、（１，１）という点は原点からの距離が\(\sqrt{2}\)で角度は\(\pi\)／４（あるいは４５°）です。

（－１，１）という点であれば原点からの距離が\(\sqrt{2}\)で角度は３\(\pi\)／４（あるいは１３５°）です。
図で見ると単純で分かりやすいでしょう。

三角関数と極座標の関係
点（ｘ,ｙ）と原点との距離と、ｘ軸から測った角度を考えます。角度は三角関数の定義を使う限りは度数法でも構いませんが、微積分を使う場合には弧度法で扱う必要があります。

極座標は、原点を中心とする円と原点を通る直線から構成される曲線座標でもあります。曲線座標のうち、最も簡単で便利でもあるものの１つです。

3次元で球面上の点と見なす場合には、後述しますように、原点からの長さに加えて角度を２つ使用します。

物理学での応用

極座標や球面座標を使う事によって、曲線の概形の把握が容易になる事や、微分方程式の解法が容易になる事があります。例えば、力学では等速円運動の分析において極座標を使うと簡単に中心力が働く事を導出できます。
また、万有引力が働くと軌道として楕円があり得るという理屈は、運動方程式を極座標変換する事で手計算で導出可能です。この時、軌道は条件によって円や放物線でもあり得る事が分かります。
（※運動方程式も含めて、微分方程式を座標変換する時はちょっとした面倒な計算が必要です。）
その他に、量子力学で水素原子の電子軌道の式を導出する時にも、基本の方程式で球面座標への変換が行われる事で手計算が可能となり、相対性理論でも時空の歪みが方向には依存しない（等方である）事を条件に課す時に座標の空間成分の一部が極座標・球面座標の形であると考えて理論が組み立てられます。

それらの微分方程式等を考える時に、強引にｘｙｚの座標で考える事も不可能ではないのですが、手計算で計算を進める事は非常に困難になるのです。

変換方法：極座標

実際に変換をする時には、三角関数（図で直感的に考えるなら三角比）を使用します。図を描いてみると次の三点で必ず直角三角形を作れる事に起因します：

  1. ある座標の点
  2. その点からｘ軸に降ろした垂線の足
  3. 原点

そこで、原点からある点までの長さをｒ、ｘ軸から測った角度をθとすると、
三角比の計算というか定義通りに、次の関係が成立します。

極座標変換の式
  • ｘ＝ｒcosθ
  • ｙ＝ｒsinθ

※この時に、θの範囲は全実数ですが、ｒは０以上の実数という事になります。

この時に、座標が負の値であっても正弦と余弦を三角関数として考えれば、正しく関係が満たされるのです。

極座標変換の式
直角三角形を作って考えます。ｘｙ平面の座標は、プラスマイナスの符号もそのままつけて考えます。

また、ｘとｙの値からｒとθを表す事もできます。

  • \(r=\sqrt{x^2+y^2}\)
  • \(\cos \theta=\Large{\frac{x}{\sqrt{x^2+y^2}} }\)\(\hspace{10pt}\sin \theta=\Large{\frac{y}{\sqrt{x^2+y^2}}}\)

※逆三角関数を使えば強引に θ＝・・・の形にもできますが、一般にはあまりメリットがありません。

高校生の方であれば、これらの関係式は暗記するのではなく、ｘとｙの式を２乗して加えるか、図の三角形の関係から直ちに理解できるように努める事が勧められます。

尚、これらの考え方は複素数の極形式の考え方に直結するものとなります。座標の原点回りの回転を考える時には複素数の極形式を使ったほうが良い場合もあります。（※回転に関しては、特にそれを群と見なす時には行列で考えたほうが良い事もあります。いずれの場合も、回転で基本となっているのは加法定理です。）

特定の関数で表された曲線を、極座標で表された点の集まりとして表示する事もできます。

例えばｙ＝ｘ２を強引に極座標で表すには、ｘ＝ｒcosθとｙ＝ｒsinθをそのまま代入すればよいのです。

すると、ｒsinθ＝ｒ２cos２θ　⇔　sinθ＝ｒ(１－sin２θ) のような関係になります。
そのような関係式を満たすｒとθの組み合わせの点の集まりが、ｙ＝ｘ２で表される放物線と全く同じものを表すという事です。

尚、半径Ｒの円の式に極座標変換を当てはめると、ｒ＝Ｒという形の式になります。
（ｒは座標の目盛で、Ｒは何かしらの定数です。ｒ＝一定の値という事です。）

ｘ２＋ｙ２＝Ｒ２にｘ＝ｒcosθとｙ＝ｒsinθを代入すると
ｒ２cos２θ＋ｒ２sin２θ＝Ｒ２
⇔　ｒ２(cos２θ＋sin２θ)＝Ｒ２
⇔　ｒ２＝Ｒ２　⇔　(ｒ－Ｒ)(ｒ＋Ｒ)＝０
ｒとＲは正の数だからｒ＝Ｒ

このように極座標で表す利点があるかないかは、その時々によって異なります。一般的には、円とか球とか、そういったぐるりと１周回るものを考える時や、周期性のあるものを考える時に極座標を使う計算上の利点がある場合が多いかとは思います。

球面座標

次に、球面座標を考えてみましょう。考え方自体は、2次元平面での極座標と同じなのです。

球面座標への変換の式
  • ｘ＝ｒsinφ cosθ
  • ｙ＝ｒsinφ sinθ
  • ｚ＝ｒcosφ

半径ｒは「球の半径」である事と、角度φの取り方に注意。
「sinφ cosθ」は、sinφ と cosθ との掛け算です。

θとφという２つの角度を使いますが、まずｚ座標から考えてみる事がポイントです。

まず「ｚ軸」「原点」「点（ｘ,ｙ,ｚ）」が作る角度をφとします。
そして、ｚ座標をｚ＝ｒcosφと表すのです。

球面座標
球面上の点を（ｘ,ｙ,ｚ）とおいて、最初にｚ座標から考えます。次に、球面上の点からｚ＝０のｘｙ平面上に垂線を下ろします。この時の「垂線の足」となる点は、球面上ではなく球面の内側に位置します。（ｒsinφ ＜ ｒ の関係に注意。）

次に、ｘｙ平面上で測った角度も必要になります。ｚ＝０での平面を考えて、この面でのｘ軸から測る角度をθとします。「ｘ軸」「原点」「球面上の点からの垂線の足（ｘ,ｙ）」が成す角をθとするという事です。

ここで、先ほどのφを使うと、原点から垂線の足までの距離はｒsinφになります。（余弦ではなく正弦になります。）

すると、ｘとｙは、「半径をｒsinφと見なした時」の平面の極座標と全く同じ考え方で表す事ができるというわけです。つまり、半径であるｒsinφに、それぞれcosθとsinθを掛ければよいという事です。

ｘ＝(ｒsinφ) cosθ ＝ｒsinφ cosθ,　ｙ＝(ｒsinφ) sinθ ＝ｒsinφ sinθ という事になり、球面座標への変換の式が完成するわけです。暗記しようと思うといかにも面倒な式ですが、図で見ると非常に単純なものを意味する式である事が分かるかと思います。

円柱座標

最後に、円柱座標についても見ておきます。これは、３次元空間の点を円柱の側面として座標を考えるという事ですが、実は発想は非常に単純です。

まず、円柱には必ず底面となる円がありますから、底面がｘｙ平面上にあるとすればｘとｙについては極座標と全く同じ式を使えます。

ではｚ座標はどうするのかというと、実は「何も変換しないでそのままｚの値を使う」というふうにします。ｚ＝ｚとするのです。この単純な発想を受け入れると、円柱座標は次のようになります。

円柱座標への変換式
  • ｘ＝ｒcosθ
  • ｙ＝ｒsinθ
  • ｚ＝ｚ

ｚ座標を無視すると、普通の平面での極座標と全く同じ形です。
場合によってはｚ＝ｈなどのように置き換えはしますが、意味は同じです。

実に単純である事が分かると思います。

円柱座標

このように、図も使ってシンプルに捉えれば難しいものではない事が理解できるでしょう。

三角関数の加法定理【証明】

恭平

三角関数の加法定理とは、三角関数の角度部分を和や差の形で表す時、個々の角度に対する三角関数の積と和などの組み合わせで計算できるという公式です。
（英：compound angle formulae）

目次：

  1. 定理の内容
  2. 証明
  3. 具体例・応用例・覚え方
  4. 外積を使った証明方法

高校数学の中では、その後に続く理論でも使うという意味では加法定理は重要な部類に入る関係式の１つであると言えます。

尚、対数関数についても「加法定理」という言葉を使用する事がありますが、ここでは三角関数についてのものを述べます。

定理の内容

■ 正弦と余弦の加法定理４式　■ 正接関数の加法定理

正弦と余弦の加法定理４式

三角関数の加法定理は、正弦・余弦・正接について存在しますが正弦と余弦の４式は次のようになります。

加法定理（正弦関数と余弦関数）

２つの角度をＡとＢとすると、次の関係式が成立します。

  1. sin(Ａ＋Ｂ)＝sinＡcosＢ＋cosＡsinＢ
  2. sin(Ａ－Ｂ)＝sinＡcosＢ－cosＡsinＢ
  3. cos(Ａ＋Ｂ)＝cosＡcosＢ－sinＡsinＢ
  4. cos(Ａ－Ｂ)＝cosＡcosＢ＋sinＡsinＢ

これらの角度の範囲は、三角関数での定義を使用するなら任意の実数になります。
負の数や２直角\(\pi\)を超える値になってもよいし、それらをＡやＢとして代入する事もできます。

これら４式について、１つの符号を反転させればもう１つの式が得られるので
「実質は正弦と余弦について１つずつ」の２つであると見なすことも可能です。

これは、－Ｂ＝＋Ｂのように考えて式をまとめても支障はないという意味です。
sin(Ａ－Ｂ)＝sin(Ａ＋(－Ｂ))＝sinＡcos(－Ｂ)＋cosＡsin(－Ｂ)＝sinＡcosＢ－cosＡsinＢ
cos(Ａ－Ｂ)＝cos(Ａ＋(－Ｂ))＝cosＡcos(－Ｂ)－sinＡsin(－Ｂ)＝cosＡcosＢ＋sinＡsinＢ
のように導出はすぐにできるので、覚えるのは４式ではなく２式でも計算はできます。

４式でやるか２式でやるかは、理解しやすいほう・覚えやすいほうの考え方でよいと思います。
１つの角度の符号を反転させて別の式の導出をするという考え方は証明でも使います。
また、証明の時に最初に証明されるのはcos(Ａ－Ｂ)の式である都合上、最初から４式で考えたほうが理解しやすいという考え方もあります。

正接関数の加法定理

正接関数にも加法定理はありますが、正接は (正弦)／(余弦)で考えれば済む事と、使用頻度が比較的少ない事からここでは参考までに記しておきます。

正接関数の加法定理

正接関数の加法定理の式は次の通りです： $$\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A\tan B}$$ $$\tan (A-B)=\frac{\tan A-\tan B}{1+\tan A\tan B}$$

これらの式は、正弦関数と余弦関数の加法定理が成立するという前提で示されます。

$$\tan (A+B)=\frac{\sin (A+B)}{\cos (A+B)}=\frac{\sin A \cos B +\cos A\sin B}{\cos A\cos B-\sin A \sin b}=\large{=\frac{\frac{\sin A}{\cos A}+\frac{\sin B}{\cos B}}{1-\frac{\sin A}{\cos A}\frac{\sin B}{\cos B}}}$$
$$\tan (A-B)=\frac{\sin (A-B)}{\cos (A-B)}=\frac{\sin A \cos B -\cos A\sin B}{\cos A\cos B+\sin A \sin b}=\large{=\frac{\frac{\sin A}{\cos A}-\frac{\sin B}{\cos B}}{1+\frac{\sin A}{\cos A}\frac{\sin B}{\cos B}}}$$

このようになる事が根拠であり、
後者の式は tan(－θ)＝tanθの関係を前者の式の結果に代入する事でも得られます。

証明

■ 考え方：三角比の範囲の場合
■ 一般角の場合①　余弦 cos (Ａ－Ｂ)の式の証明
■ 一般角の場合②　残り３式の導出　

考え方：三角比の範囲の場合

証明はいきなり一般の角度の場合でもできるのですが、まず図形上の考え方を見るために０°～９０°の範囲における三角比の中で加法定理が成立する事の説明をしましょう。

図のように単位円の「第１象限」の部分で２つの角度の考えて三角形を作ります。
ここで、２つの角度の差を考えます。図で言うと\(\alpha－\beta\) です。
具体的な角度を入れるなら、例えば６０°－１５°＝４５°などを考えています。

その差をとった角度の正弦や余弦をどのように考えるのかというと、図のように点Ａから点Ｂまでの距離をもとの正弦と余弦で表し、さらに△ＡＯＢに余弦定理を使用するのです。この時、線分ＡＢの距離は三平方の定理で計算できます。

線分ＡＢの長さは三平方の定理で計算できます。

余弦定理で組み立てた式に三角比の公式 sin２θ＋cos２θ＝１ を適用すると、余弦に関する加法定理の関係式cos(Ａ－Ｂ)＝cosＡcosＢ－sinＡsinＢが得られるのです。

これはとりあえず０°～９０°の範囲の図形的な位置関係から関係式を導出するものですが、じつは三角関数として実数全体の範囲で一般の角度を考える場合でも、基本的な考え方は同じなのです。

  • ２つの角度の２つの三角形を作り、その角度の差によりもう１つの三角形を考える。
  • 三角形は、単位円周上の２点と原点で構成する。
  • 円周上の２点間の距離を三平方の定理で表し、さらに余弦定理を適用する。

この基本的な考え方のもとで証明をしていきます。
尚、その場合だと得られるのは余弦の「差」に関するcos (Ａ－Ｂ)の式になりますが、その式が証明されると変数の置き換えで残り３式も証明されるという形になります。

一般角の場合①　余弦 cos (Ａ－Ｂ)の式の証明

実数全体を範囲とする拡張された角度（一般角）でも加法定理が成立する事の証明は、一般的には次のように座標上の単位円周上の２点を考えて角度を統一的に扱います。

考え方自体は三角比の範囲の時と同じで、２点の「長さ」（プラスの値）を上手に使うのです。

まず単位円周上の２点（ｘ１,ｙ１）と（ｘ２,ｙ２）を考え、
これらの座標を（cosＡ,sinＡ）および（cosＢ,sinＢ）とおいてもよい事から始めます。
つまり(１,０)から２点まで測った角度をそれぞれＡおよびＢとしています。

このときの２点の位置関係は、ｘ座標で言うとどちらがどちらよりも大きくても（あるいは等しくても）構わず、むしろどちらの場合でも統一的に扱って証明の計算を進められる事がポイントです。

つまり、鋭角の場合・鈍角の場合・負の角度の場合・・といった場合分けをしなくてもよいという事です。

余弦の場合は、負の角度を代入しても同じ絶対値の正の角度を代入した時と同じ値である事【cos(－θ)＝cosθ】もポイントです。結論を言うと、加法定理のうち余弦の cos(Ａ－Ｂ)に着目するととうまくいくのです。

単位円周上の２点と原点で作られる三角形に注目します。この時に原点を頂点とする部分の角度はＡ－Ｂになります。（これは円周上の２点の位置関係によってプラスの値にもマイナスの値にもなります。）

この三角形に、余弦定理を適用します。余弦定理は辺の長さと１つの余弦に関して、実数全体の範囲の角度で正しい関係式を作ります。

★２点の座標をベクトルと考えて
「ベクトルの長さと内積は回転によって不変だから」・・という論法でやる事も可能です。

２点の長さの出し方は三角比の範囲の時と同じで三平方の定理を使います。（座標上の２点の距離の一般的な計算方法でもあります。）余弦定理で必要なのは２乗の形なので、長さを２乗した形は次のようになります。

(cosＡ－cosＢ)２＋(sinＡ－sinＢ)２
＝cos２Ａ＋cos２Ｂ－２cosＡcosＢ＋sin２Ａ＋sin２Ｂ－２sinＡsinＢ
＝２－２cosＡcosＢ－２sinＡsinＢ

【cos２Ａ＋sin２Ａ＝１、cos２Ｂ＋sin２Ｂ＝１なのでこのように式が簡単になります。】

他方、三角形の残りの２辺は単位円の半径ですから長さはともに１です。この条件のもとで余弦定理を考えてみると次のようになります。

(cosＡ－cosＢ)２＋(sinＡ－sinＢ)２＝１２＋１２－２・１・１・cos(Ａ－Ｂ)
⇔２－２cosＡcosＢ－２sinＡsinＢ＝１＋１－２cos(Ａ－Ｂ)
⇔ cos(Ａ－Ｂ)＝cosＡcosＢ＋sinＡsinＢ

【最後の式変形は両辺にある定数の「２」を消し、さらに両辺をー２で割り整理したものです。】

このように、加法定理のうち余弦の「差の形」のものが成立する事が分かります。この形は２乗の展開式に由来するものというわけです。また、角度の差をとる時に２つの項がプラスで結ばれる理由も証明の過程から比較的明確であるかと思います。２点間の距離の計算による２乗の展開式由来なので同符号というわけです。

この場合の角度には、三角関数の変数としての実数全体の範囲の任意の角度を代入しても成立します。これは余弦定理が実数全体の範囲で角度を代入した場合にも正しい関係式を作っているためです。円周上の２点と原点が同一直線上に並んで「三角形を作らない」場合にでも点同士の距離と余弦関数の値の正しい関係を表しています。

一般角の場合②　残り３式の導出

正弦と余弦に関する加法定理の残り３式はどのように導出するのかというと、それらはcos(Ａ－Ｂ)＝cosＡcosＢ＋sinＡsinＢをもとに出すのです。

まず、Ｂがプラスでマイナスであってもこの関係式は成立しますから、Ｂの部分を－Ｂに置き換えるとcos(Ａ＋Ｂ)＝cosＡcos(－Ｂ)＋sinＡsin(－Ｂ)＝cosＡcosＢ－sinＡsinＢとなります。

正弦のほうはどうするのかというと、ＢをＢ＋\(\pi\)／２に置き換えます。

cos(Ａ＋Ｂ＋\(\pi\)／２)＝cosＡcos(Ｂ＋\(\pi\)／２)－sinＡsin(Ｂ＋\(\pi\)／２)＝－cosＡsinＢ－sinＡcosＢ

他方で cos(Ａ＋Ｂ＋\(\pi\)／２)＝－sin(Ａ＋Ｂ) でもあるので、

－sin(Ａ＋Ｂ)＝－cosＡsinＢ－sinＡcosＢ⇔sin(Ａ＋Ｂ)＝sinＡcosＢ＋cosＡsinＢ

正弦の残り１式は、sin(Ａ＋Ｂ) のＢを－Ｂに置き換えて得ます。sin(Ａ＋Ｂ)＝sinＡcos(－Ｂ)＋cosＡsin(－Ｂ)＝sinＡcosＢ－cosＡsinＢ です。

これによって、正弦関数と余弦関数の加法定理４式が確かに成立する事になります。

参考までに、三角比の範囲の場合に cos(Ａ－Ｂ)のＢを－Ｂに置き換えてcos (Ａ＋Ｂ)にした場合の図形的意味は次図のようになります。これを一般化しているのが、三角関数で考えた一般の角度での加法定理です。単位円周上で考えれば、同様の図形的な位置関係を必ず作る事ができます。

三角比の範囲で考えた場合の cos(Ａ＋Ｂ)の図形的な解釈の１つです。三角関数の加法定理において角度部分を ｘ → －ｘ に置き換える操作は単に形式上そうできるというだけではなく、図形上の意味にも必ず対応しています。

具体例・応用例・覚え方

具体例についても見てみましょう。

例えば、９０°＝６０°＋３０°、９０°＝４５°＋４５°といった関係を加法定理は正しく表すでしょうか？

$$\sin\left(\frac{\pi}{3}+\frac{\pi}{6}\right)=\sin\left(\frac{\pi}{3}\right)\cos\left(\frac{\pi}{6}\right)+\cos\left(\frac{\pi}{3}\right)\sin\left(\frac{\pi}{6}\right)$$

$$=\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{2}+\frac{1}{2}\cdot\frac{1}{2}=\frac{3}{4}+\frac{1}{4}=1$$

$$\sin\left(\frac{\pi}{3}+\frac{\pi}{6}\right)=\sin\left(\frac{\pi}{2}\right)=1 で一致します。$$

４５°のほうでやってみても同じで、

$$\sin\left(\frac{\pi}{4}+\frac{\pi}{4}\right)=\sin\left(\frac{\pi}{4}\right)\cos\left(\frac{\pi}{4}\right)+\cos\left(\frac{\pi}{4}\right)\sin\left(\frac{\pi}{4}\right)$$

$$=\frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{2}}\cdot\frac{1}{\sqrt{2}}=\frac{1}{2}+\frac{1}{2}=1$$

こういう形で成立するわけです。

１２０°－６０°＝６０°の場合を今度は余弦のほうでやってみると、

$$\cos\left(\frac{2\pi}{3}-\frac{\pi}{3}\right)=\cos\left(\frac{2\pi}{3}\right)\cos\left(\frac{\pi}{3}\right)+\sin\left(\frac{2\pi}{3}\right)\sin\left(\frac{\pi}{3}\right)$$

$$=-\frac{1}{2}\cdot \frac{1}{2}+\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{2}=-\frac{1}{4}+\frac{3}{4}=\frac{1}{2}=\cos\left(\frac{\pi}{3}\right)$$

加法定理が成立するなら、既知の三角関数の値を使って例えば４５°－３０°＝１５°といった半端な角度の正弦や余弦の値も分かるはずです。「１５°」における正弦の値を加法定理で計算すると次のようになります。

$$\sin\left(\frac{\pi}{12}\right)=\sin\left(\frac{\pi}{4}-\frac{\pi}{6}\right)=\sin\left(\frac{\pi}{4}\right)\cos\left(\frac{\pi}{6}\right)-\cos\left(\frac{\pi}{4}\right)\sin\left(\frac{\pi}{6}\right)$$

$$=\frac{1}{\sqrt{2}}\cdot\frac{\sqrt{3}}{2}-\frac{1}{\sqrt{2}}\cdot\frac{1}{2}=\frac{\sqrt{6}}{4}-\frac{\sqrt{2}}{4}=\frac{\sqrt{6}-\sqrt{2}}{4}$$

この計算値は約 0.2588 で、マクローリン展開で計算した値にほぼ一致します。

４５°＋４５°や６０°＋６０°のような場合は、より一般的にＡに対する２Ａとして「倍角の公式」の形にして捉える事も可能です。和積の公式や積和の公式も、加法定理の幾つかの式を組み合わせて変形したものです。

三角関数の微分公式の証明でも、加法定理を使用して計算を進めます。

加法定理の式の形の「覚え方」としては、複素数を利用する方法もあります。【これらは「説明」や「覚え方」としては有用ですが「証明」にはならないので注意。】

複素数の場合、指数関数表示（オイラーの公式）からｅｉ(θ＋φ)＝ｅｉθｅｉφですが、
cos(θ＋φ)＋ｉsin(θ＋φ)＝(cosθ＋ｉsinθ)(cosφ＋ｉsinφ)
＝cosθcosφ－sinθsinφ＋ｉ(sinθcosφ＋cosθsinφ)
を意味しますから、実部と虚部の値を比較すれば
cos(θ＋φ)＝cosθcosφ－sinθsinφ、sin(θ＋φ)＝sinθcosφ＋cosθsinφ
の関係が成立している事が分かります。
これらは三角関数の加法定理の内容そのものです。

（これはド・モアブルの定理で考えても同じです。
ただし、その定理の証明に加法定理が使用されているので、「加法定理の証明」としては
適切とは言えないのです。）

外積を使った証明

加法定理の別の証明方法として、３次元ベクトルの外積（ベクトル積、クロス積）を使う方法があります。

外積ベクトルは３次元のベクトルに対して考えるものですが、ｚ＝０としたｘｙ平面上の２つのベクトルに対して考える事は一応可能です。

そこで、次の２つのベクトルを考えます。
（角度θとφはプラスの値とします。ベクトルの大きさはどちらも１である事にも注意。）

$$\overrightarrow{a}=\cos\theta\hspace{2pt}\overrightarrow{e_1}+\sin\theta\hspace{2pt}\overrightarrow{e_2},\hspace{10pt}\overrightarrow{b}=\cos\phi\hspace{2pt}\overrightarrow{e_1}-\sin\phi\hspace{2pt}\overrightarrow{e_2}$$

$$\overrightarrow{e_1}=(1,0,0),\hspace{10pt}\overrightarrow{e_2}=(0,1,0),\hspace{10pt}（本当は\overrightarrow{e_3}=(0,0,1)もある。）$$

負の角度を使っても同じ事ですが、ここではプラスの値の角度の正弦にマイナス符号をつけた形で座標を表すとします。

そこで外積ベクトルを考えてみましょう。（外積について成立する公式を使用します。）

$$\overrightarrow{a}×\overrightarrow{b}=(\cos\theta\hspace{2pt}\overrightarrow{e_1}+\sin\theta\hspace{2pt}\overrightarrow{e_2})×(\cos\phi\hspace{2pt}\overrightarrow{e_1}-\sin\phi\hspace{2pt}\overrightarrow{e_2})$$

$$=-\cos\theta\sin\phi(\overrightarrow{e_1}×\overrightarrow{e_2})+\sin\theta\cos\phi(\overrightarrow{e_2}×\overrightarrow{e_1})$$

$$=-\cos\theta\sin\phi(\overrightarrow{e_1}×\overrightarrow{e_2})-\sin\theta\cos\phi(\overrightarrow{e_1}×\overrightarrow{e_2})$$

$$=-(\cos\theta\sin\phi+\sin\theta\cos\phi)(\overrightarrow{e_1}×\overrightarrow{e_2})$$

$$=(\cos\theta\sin\phi+\sin\theta\cos\phi)(-\overrightarrow{e_3})$$

他方で、この外積ベクトルは定義通りに考えれば向きは「ｚ軸のマイナス方向」であり、
大きさは\(|\overrightarrow{a}||\overrightarrow{b}|\sin(\theta+\phi)=\sin(\theta+\phi)\) です。

という事は、

$$\overrightarrow{a}×\overrightarrow{b}=\sin(\theta+\phi)\hspace{2pt}(-\overrightarrow{e_3})$$

という事でもありますから、２つの結果を等号で結べます。

$$(\cos\theta\sin\phi+\sin\theta\cos\phi)(-\overrightarrow{e_3})=\sin(\theta+\phi)(-\overrightarrow{e_3})$$

$$よって、\sin\theta\cos\phi+\cos\theta\sin\phi=\sin(\theta+\phi)【加法定理の証明終り】$$

この場合は、正弦の加法定理が直接示されています。（証明の最後の箇所では見やすいように項の順番だけ入れ替えています。）これを使って残りの３式も証明が可能です。

ここで行った計算は一体何なのかというと、前半で記した証明が三角形の「辺の長さ」を考えたのに対して、この外積を使った証明では平行四辺形の「面積」（三角形でも可能）を使ったという事です。本質的には、座標を使って証明するという同じ部類の２つの証明法と言えます。

余弦定理

恭平

余弦定理とは、三角形の３辺と１つの角の余弦について成立する関係式です。
（英：cosine rule）

特別な場合として余弦定理を直角に対して適用すると三平方の定理の形になります。
（ただし、余弦定理一般を証明するには普通は三平方の定理を使います。）

目次：

  1. 定理の内容
  2. 証明①：鋭角の場合
  3. 証明②：鈍角の場合
  4. 角度の範囲が実数全体の場合

★三角比の余弦（コサイン）と三角関数の余弦関数については別途に述べています。

定理の内容

余弦定理の内容は次のようなものです。

余弦定理

三角形ＡＢＣの辺の長さをＢＣ＝ａ、ＡＣ＝ｂ、ＡＢ＝ｃとして、
∠ＢＡＣ＝θ（長さａの辺ＢＣの対角）とする時、次の関係式が成立します。 $$a^2=b^2+c^2-2bc\cos \theta$$ θは鋭角でも鈍角でも成立し、
θ が直角の時には三平方の定理ａ２＝ｂ２＋ｃ２になります。
また、θ＝０、\(\pi\)の場合は３点が１直線上に並んでいる場合であり、
座標上などで角度に向きをつけている場合には負の角度を代入しても正しい関係式を表します。

三角形のある１辺の具体的な値を知りたい時には「２辺の長さと１つの角度の『余弦』の値が分かれば計算は可能である」という事が、余弦定理の意味と使い方です。

定理の内容

余弦定理を証明する一番シンプルな方法は三平方の定理を使う方法です。（三平方の定理は相似条件・合同条件といった条件だけで証明できます。）

ここでは、対象の角の大きさが鋭角か鈍角で場合分けをして証明します。
式変形も含めてやや詳しく説明していますが、要するに三平方の定理を適切に適用すると関係式を導出できるというのが証明の流れになります。

証明①：鋭角の場合

まず対象の角度の大きさが鋭角の場合です。

この場合、もう１つの角についても鋭角か鈍角かで場合分けしますが、得られる結果は同じになります。どちらの場合でも、三角比の関係を使って上手に直角三角形の辺の関係を作ります。

下図で、∠ＢＡＣ＝θが鋭角のもとで、∠ＡＢＣが鋭角か鈍角かを見ます。

∠ＡＢＣが鋭角の場合（図の上側）、直角三角形を作るように線分ＡＢを延長して点Ｈをとります。この時、直角三角形である△ＡＣＨの底辺部分ＡＨの長さは余弦を使ってｂcosθで表せます。

鋭角の場合の証明

他方、高さ部分もＣＨ＝ｈは正弦を使ってｈ＝ｂsinθと表せますが、単純にこれに三平方の定理を適用してもじつはうまくいきません。そこで、△ＡＣＨだけでなく、△ＢＨＣも直角三角形である事に注目します。すると、ＢＨ＝ｂcosθ－ｃになる事に注するとうまくいきます。

ＢＨ２＋ｈ２＝ａ２ ⇔ (ｂcosθ－ｃ)２＋ｈ２＝ａ２

他方、△ＡＣＨについてＡＨ＝ｂcosθ 、ＣＨ＝ｈのもとで三平方の定理を適用します。

(ｂcosθ)２＋ｈ２＝ｂ２　⇔　ｈ２＝ｂ２－ｂ２cos２θ

つまり、未知数のｈは代入して消す事ができます。

(ｂcosθ－ｃ)２＋ｈ２＝ａ２ に ｈ２＝ｂ２－ｂ２cos２θを代入すると、ｂ２cos２θ－２ｂｃcosθ＋ｃ２＋ｂ２－ｂ２cos２θ＝ａ２
⇔ ａ２＝ｂ２＋ｃ２－２ｂｃcosθ　【ｂ２cos２θの項が消えてあとは順番だけ整理しただけです。】

つまりこの場合では余弦定理が確かに成立する事になります。

次に∠ＢＡＣ＝θと∠ＡＢＣが両方とも鋭角の場合（図の下側）には、点Ｃから辺ＡＢに垂線を下ろせます。その垂線の足をＨとおきます。この場合も先ほどとやり方自体は同じで、△ＡＨＣと△ＣＨＢの２つが直角三角形になり、ＣＨ＝ｈとして余弦と組み合わせて三平方の定理で関係式を作ります。

ＡＨ＝ｂcosθ、ＣＨ＝ｈ、ＢＨ＝ｃ－ＡＨ＝ｃ－ｂcosθ のもとで、

(ｂcosθ)２＋ｈ２＝ｂ２　かつ　(ｃ－ｂcosθ)２＋ｈ２＝ａ２　

前者のほうの式を後者のほうの式にｈ２を代入して消します。
(ｃ－ｂcosθ)２＋ｂ２－(ｂcosθ)２＝ａ２ ⇔ ａ２＝ｂ２＋ｃ２－２ｂｃcosθ

よって、この場合でも余弦定理が確かに成立する事になります。

証明②：鈍角の場合

では、∠ＢＡＣが鈍角の場合はどうするかというと、この場合には余弦に鈍角を入れる必要があるので三角関数として余弦を考える必要があります。結論を先に言うとcos(ｘ＋\(\pi\)／２）＝－sinｘの公式を使います。この関係を認めるうえで、余弦定理の形で辺の長さの関係を表せるという事です。

この時、鋭角である角度 φ を使って、θ ＝ φ＋９０°と表すとこの時の証明はしやすいです。ただ、三角関数を使うので、ここで角度は弧度法で表してθ ＝ φ＋\(\pi\)／２と書く事にします。

この時、図のように△ＡＢＰが直角三角形になるように便宜上の点ＰをＢＣ上において、∠ＡＢＰが直角、∠ＰＢＣ＝φ（鋭角）であると捉えます。（図の位置関係はθが鋭角の場合と少し変えて描いています。）

鈍角の場合の証明

ここで、θ＝∠ＰＢＣ＋∠ＡＢＰ＝φ＋\(\pi\)／２です。この時、ＡＢを延長しＣからその延長線に垂線を下ろして垂線の足をＨとします。

平行線の錯角の関係により∠ＢＨＣ＝∠ＰＢＣ＝φである事に注意し、△ＢＨＣは直角三角形なのでＢＨ＝ｂsinφ、ＣＨ＝ｂcosφと表せます。ここで△ＡＨＣも直角三角形なので三平方の定理で関係式を作ると次のようになります。

(ｃ＋ｂsinφ)２＋(ｂcosφ)２＝ａ２ ⇔ ｃ２＋２ｂｃsinφ＋ｂ２sin２φ＋ｂ２cos２φ＝ａ２

ここでまず、sin２φ＋cos２φ＝１の公式により
ｂ２sin２φ＋ｂ２cos２φ＝ｂ２(sin２φ＋cos２φ)＝ｂ２

すると、ｃ２＋２ｂｃsinφ＋ｂ２＝ａ２

「余弦」定理の証明なのに正弦が出てきてしまったという話ですが、cosθ ＝ cos(φ＋\(\pi\)／２)＝－sinφ　つまりsinφ＝－cosθとなるので、ａ２＝ｂ２＋ｃ２－２ｂｃcosθ　となり、この場合も余弦定理が成立します。

これは三角関数の定義に従って余弦の値を決める時に成り立つもので、具体的な鈍角の値を余弦関数に入れると必ず負の値ですから、符号は必ず反転してプラスになる事に注意する必要もあります。

例えば１２０°（２\(\pi\)／３ [rad]） を角度として代入するなら、
ａ２＝ｂ２＋ｃ２－２ｂｃ・(－１／２)＝ｂ２＋ｃ２＋ｂｃ　のようになります。

理解の仕方としては、θが鋭角であろうと鈍角であろうと、三角関数の定義に従って余弦の値を考える限りは気にせずに余弦定理を使って計算をしてよい、という事になります。

角度の範囲が実数全体の場合

三角関数の定義域（実数全体）を当てはめるのであれば、上記以外の場合にはどうなるでしょう？

まず鋭角でも鈍角でもない角度として「直角」がありますが、これは冒頭でも触れた通り三平方の定理そのものになりますので、別途に証明できて成立します。

次に、０と１８０°（\(\pi\)）の場合ですが、仮に成立するとすると次のような式になります。

θ＝０とき、ａ２＝ｂ２＋ｃ２－２ｂｃ＝(ｂ－ｃ)２　より、ａ＝ｂ－ｃまたはｃ－ｂ

θ＝\(\pi\)のとき、ａ２＝ｂ２＋ｃ２＋２ｂｃ＝(ｂ＋ｃ)２　より、ａ＝ｂ＋ｃ

（もちろん、ａ≧０、ｂ≧０、ｃ≧０という条件のもとでこうなります。）

問題はこれに図形的な意味があるかという事ですが、じつは確かにあります。これらはいずれも、３点Ａ、Ｂ，Ｃが一直線上に並んだ時にあり得る関係式です。そのため、これらの角度においては「三角形はできない」という図形的な意味付けをするのであれば、各点間の距離を表す式として余弦定理は確かに成立すると言えます。

一般の角度の場合
余弦定理を使う時には、通常の平面幾何的な意味では０°＜θ＜１８０°の範囲だけを考えればよいのですが、図形的な意味を拡張してそれ以外の値を代入する事も可能です。

では、１８０°（\(\pi\)）を超える場合はどのように考えられるでしょう。この場合、三角関数の考え方では負の角度が０～－\(\pi\)の場合と同じなので負の角度の場合を考えると、余弦関数の値はマイナス符号をつけない正の値の時と同じ値です。cos(－θ)＝cosθと、三角関数では定義されます。

このような場合に図形上での意味としては、座標やベクトルの関係において角度に反時計回り・時計回りの区別をつける時の事が想定できます。しかしその場合でも「２点間の距離」自体は正の値として考えます。例えば座標上でｘ軸に平行な直線に関して図形を反転させた場合に、座標の符号が変わる事はあっても各点を結ぶ辺の「長さ」自体は変わりません。

この事が、負の値を角度として適用した場合の図形的な意味になります。０≦θ≦\(\pi\) の場合には余弦定理は適用可能ですから、－θを考えた時には cos(－θ)＝cosθ により角度が正の値の時と全く同じ辺の長さの関係式になります。これが、「底辺を軸として三角形を反転させた時にも辺の『長さ』自体については変わらない」事に対応するのです。この意味において、座標上などで角度に向きをつける場合でも、辺の長さの関係だけを問題にする時には余弦定理に負の角度を入れても正しく関係式を作れるという事です。

★言い換えると、余弦定理だけからは「正負の符号も含めた」意味での座標の位置関係を確定させる事はできず、基本的には長さについてのみ計算可能な関係式であるとも言えます。これは三平方の定理と同様の性質です。

\(\pi\)を超える角度の図形的な意味は負の角度の場合と同じとすると、これも余弦定理の角度部分に代入しても三角形の辺の長さの関係は正しく表されている事になります。

三角関数の周期性により、３６０°（２\(\pi\)）を超える角度では１周して全く同じ点に戻るという図形的な解釈のもとでは、それらの角度を代入したとしても同じく三角形の辺の長さの関係は同じく正しく表されます。

以上から、余弦定理は一般的な鋭角、鈍角、直角の三角形を考える場合にも、図形上の適切な意味付けを与える限りにおいては実数全体を余弦の角度として代入しても成立する関係式である、という事になります。