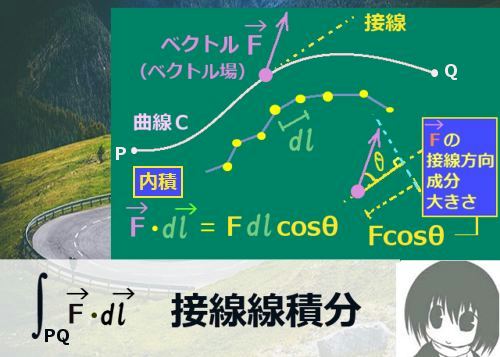
電磁気学や流体力学、数学のベクトル解析の分野で、ガウスの発散定理と並んで重要な定理とも言えるストークスの定理について、その内容・使い方・証明を詳しく説明します。
ストークスの定理はベクトル場に対する数学上の定理です。
スートクスの公式と呼ばれる事もあります。
ストークスの定理とは?内容とイメージ
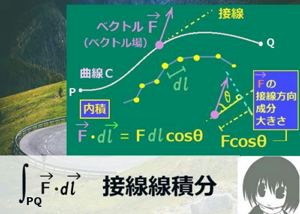
ストークスの定理は、ベクトル場の接線線積分と、ベクトル場の回転に対する法線面積分を等式で結びつける事ができるという数学上の定理です。その内容と証明について詳しく説明します。
定理の内容と表記
ベクトル場の変数x、y、zは独立変数で、ベクトル場の回転の計算(偏微分含む)もまずその条件下で行われます。次に、対象となる関数を積分する時点で曲面上あるいは曲線上という制約がつく…すなわちz=z(x,y)といった形の式が一部の変数に代入されて互いに独立ではなくなるとします。
$$ベクトル場は\overrightarrow{F}=(F_1(x,y,z),F_2(x,y,z),F_3(x,y,z))であるとします。$$
$$曲面S上でz=z(x,y)という制約がつく時は$$
$$F_1(x,y,z)=F_1(x,y,z(x,y))のように記す事にします。$$
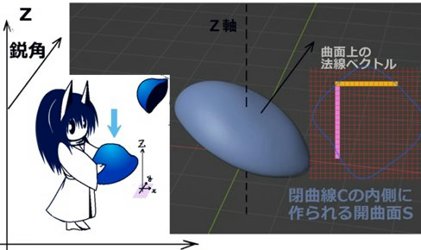
空間内の閉曲線 C に対して、
そのCを外周として共有する任意の開曲面 S に対して
ベクトル場の接線線積分と法線面積分についての次の式が成立します。
$$\oint_C\overrightarrow{F}\cdot d\overrightarrow{l}=\int_S\mathrm{rot}\overrightarrow{F}\cdot d\overrightarrow{s}$$
ただし右辺のベクトル場の回転の計算はx、y、zが独立変数であるという条件下で行われ、
法線面積分を考えた時点で「\(\mathrm{rot}\overrightarrow{F}\)」という関数全体に対して曲面S上という制約がつきます。
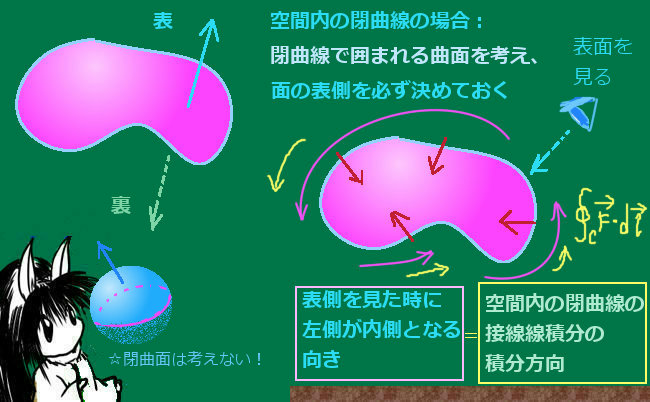
接線線積分を考える C は閉曲線ですが、曲面 S は閉曲面ではなく開曲面を考えます。
開曲面Sの表裏は、接線線積分の積分方向に合わせて決まります。
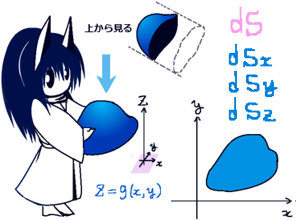
\(d\overrightarrow{s}\) =(dsx,dsy,dsz)のもとで、
曲面Sのyz平面、xz平面、xy平面への射影をそれぞれSyz, Sxz, Sxy とします。
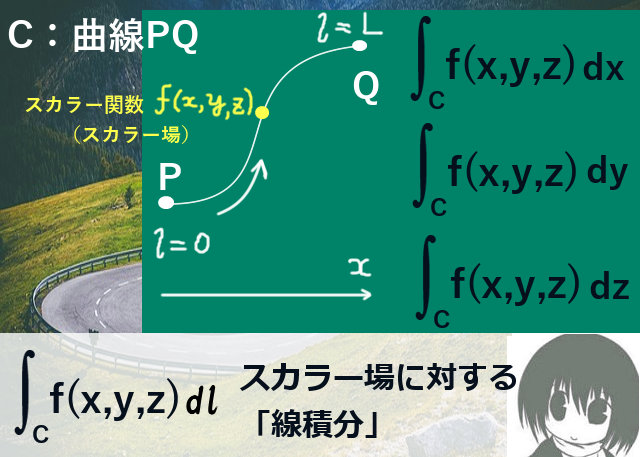
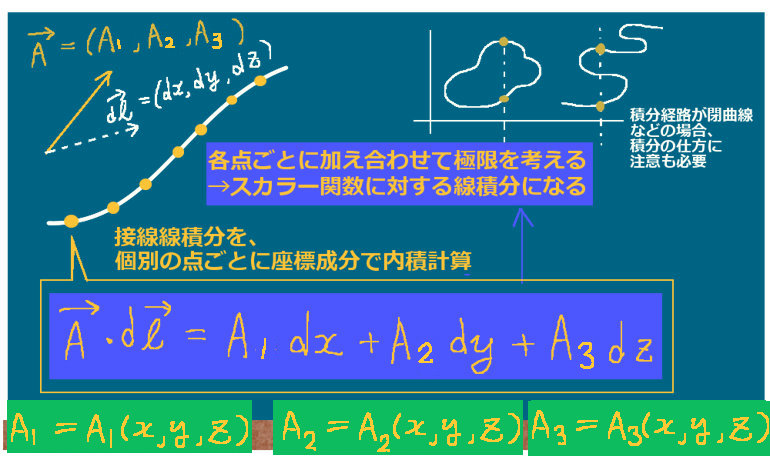
上式の左辺のベクトル場に対する接線線積分をスカラー場(ここではベクトル場の成分)に対する線積分に分解した場合には、次の3式が成立します。
【左辺はそれぞれxのみの関数、yのみの関数、zのみの関数とします。】
$$\int_C F_1(x)dx=\int_{Sxz}\frac{\partial F_1(x,y,z)}{\partial z}ds_y-\int_{Sxy}\frac{\partial F_1(x,y,z)}{\partial y}ds_z $$
$$\int_C F_2(y)dy=\int_{Sxy}\frac{\partial F_2(x,y,z)}{\partial x}ds_z-\int_{Syz}\frac{\partial F_2(x,y,z)}{\partial z}ds_x $$
$$\int_C F_3(z)dz=\int_{Syz}\frac{\partial F_3(x,y,z)}{\partial x}ds_x-\int_{Sxz}\frac{\partial F_3(x,y,z)}{\partial z}ds_y $$
これらスカラー関数の線積分に関する3式の右辺は、
ベクトル場の回転のx成分そのものではなくて、「ベクトル場の回転の各成分に含まれる項を組み合わせた式」です。
例えばxに関する偏微分はベクトル場の回転の第2成分と第3成分に含まれていて、そこから取ってきて組み合わせています。
また、これら3式の両辺を加え合わせると、もとのベクトル場の接線線積分に対するストークスの定理の形になります。

「ベクトル場の回転」はベクトルです。次のように偏微分を使って表されます。
「ベクトル場の発散」はスカラーである事との違いに少し注意。$$\mathrm{rot}\overrightarrow{F}=\left( \frac{\partial F_3}{\partial y}-\frac{\partial F_2}{\partial z} ,\hspace{5pt} \frac{\partial F_1}{\partial z}-\frac{\partial F_3}{\partial x} ,\hspace{5pt} \frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial y} \right)$$
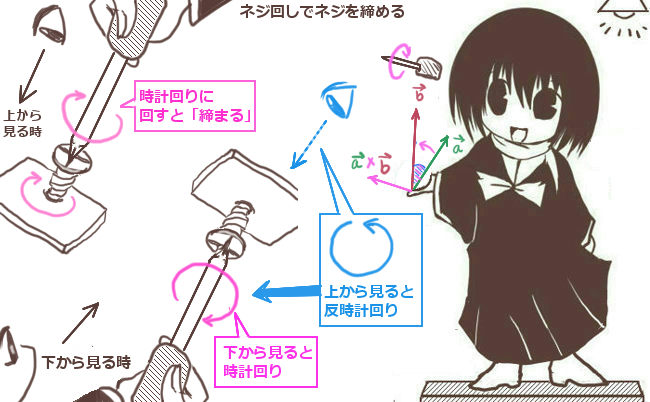
ストークスの定理を適用する事で、ベクトル場の回転は「閉曲線の接線線積分」という文字通りの「回転」するイメージの図形的な意味を持つと解釈する事が可能になります。
のちの証明での計算のための注意点を挙げますと、ベクトル場の「回転」における偏微分は3変数x,y,zを独立変数として扱って計算をするものです。つまり、xで偏微分するならyとzは単純に定数扱いするという意味です。
それに対して、「曲面上のベクトル場」「曲線上のベクトル場」という条件が付くと3変数は独立では無く、曲面上であれば2変数だけが独立、曲線上であれば3変数とも従属関係という事になります。これが証明の1つにおける計算では重要になります。
積分の表記方法についての注記
ストークスの定理は、ガウスの発散定理と比較すると数学的な内容は少し込み入っています。
積分の表記方法は書籍などによって異なる事がありますが、この記事では数式の表現を明確にするために1つの表記方法に統一をします。
この記事では、紛らわしさを避けるために「プライスマイナスの符号がついた面積要素」を考える面積分(法線面積分およびその成分によるスカラー関数の積分)を表すときには積分記号は1つだけつけて、二重積分として累次積分(1変数の場合の定積分計算の繰り返し)によって計算してよい事を表すときには積分記号を2つ付けています。積分する領域全体を表すSなどの記号はどちらの場合でも適宜使用しています。$$面積分(面積要素に符号がある):\int_{Sxz}\frac{\partial F_1(x,y,z)}{\partial z}ds_y$$
$$二重積分(累次積分が可能):\int\int_{Sxz}\frac{\partial F_1(x,y,z)}{\partial z}dxdz$$
この例ではSは曲面上の領域で、Sxzはxz平面上の領域です。
面積要素を積分変数とする場合には、曲面の場所によってプラスマイナスの符号が入れ替わる事があります。そのため、法線ベクトルの成分を積分変数とする時でも領域は曲面であると記すようにしています。
二重積分を累次積分で計算できる形で書いた時には、平面上の点に対応するスカラー関数の積分を行えばよいという事で領域を平面と考えて問題ない事になります。
書籍によっては面積分に対しても積分記号を2つ付けている事もあり、表記方法は一定していませんがこの記事では混同を避けるために表記方法を統一するという事です。
面積分の積分変数のプラスマイナスの符号の扱いについても表記方法をここで明確にしておきます。面積分の場合は表面と裏面とで面積要素ベクトルの向きが逆であり、つまり「プラスマイナスの符号が異なる」事になります。
累次積分(1変数の定積分計算を続けて行う)として二重積分を計算する場合には、
最終的な積分の結果が領域の分割の方法には依存しない事から
|dsx|=|dydz|
|dsy|=|dxdz|
|dsz|=|dxdy|
と考えて、積分の中で置き換える事ができます。
ここで絶対値記号をつけているのは、状況によって符号の違いがある事を表しています。
曲面の表側と裏側の設定等により、例えばdsz=dxdyで計算できる場合と、
dsz=-dxdyとする必要がある場合があります。$$ds_y=dxdzの場合:$$
$$\int_{Sxz}\frac{\partial F_1(x,y,z)}{\partial z}ds_y=\int\int_{Sxz}\frac{\partial F_1(x,y,z)}{\partial z}dxdz$$
$$ds_y=-dxdzの場合:$$
$$\int_{Sxz}\frac{\partial F_1(x,y,z)}{\partial z}ds_y=-\int\int_{Sxz}\frac{\partial F_1(x,y,z)}{\partial z}dxdz$$
図形的なイメージ
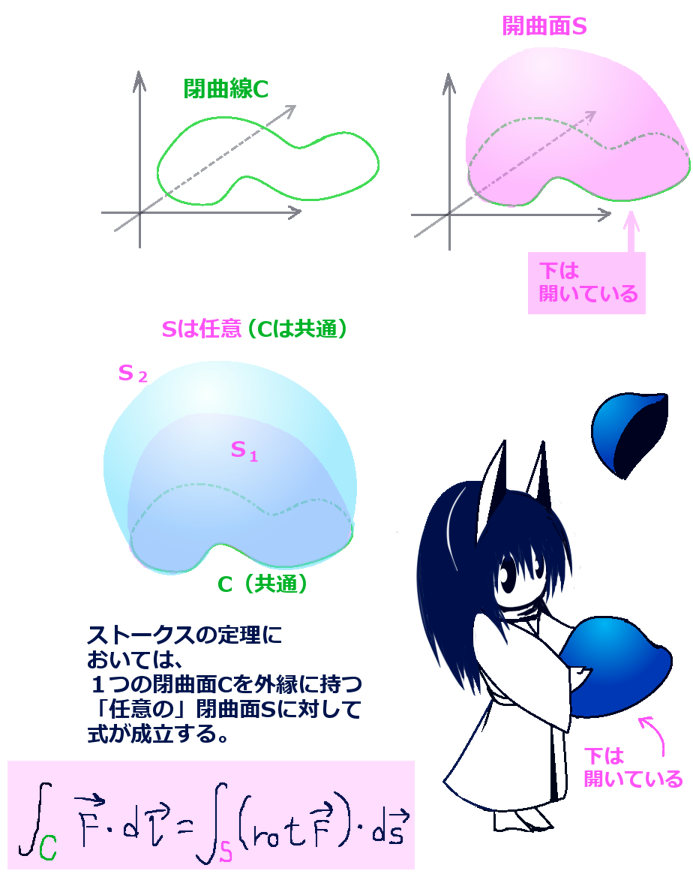
ストークスの定理の図形的なイメージは次のような感じです。
まずループ状に閉じた閉曲線 C があります。
その内側に膜が張ってあって、「閉曲面にはしない」という条件で任意の曲面の形に変形させる事ができるとします。
その時に「どんな形の曲面 S についてもストークスの定理の形の式が成立する」・・という事です。
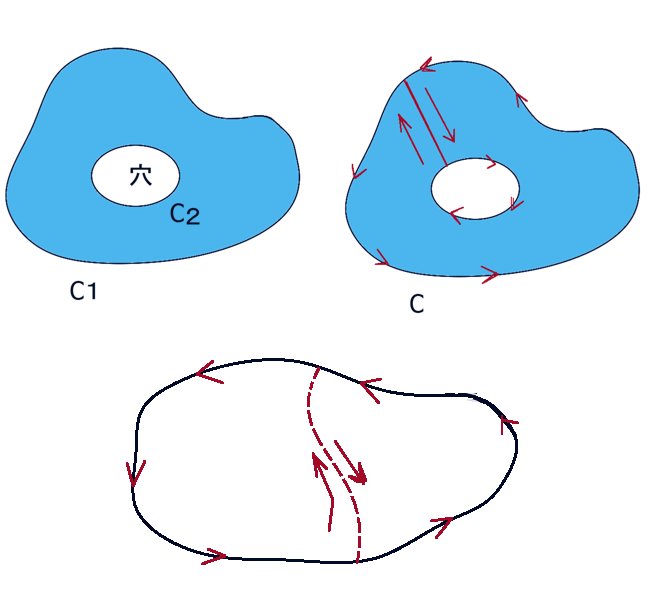
では、開曲面Sには穴のような破れがあった場合はどうでしょうか。
実はその場合でもストークスの定理は成立します。穴を作る閉曲線と元の閉曲線を1本の線で結ぶと大きな1つの閉曲線が作られるためです。付け足してしまった線については、その線を向きだけが異なる2つの線が重なっていると考えるとその線上での接線線積分の合計は「プラスマイナスが打ち消して」ゼロになって積分の値に影響しません。
ただし、そのような場合には「穴」を構成する部分について接線線積分の向きを全体の接線線積分の向きに合わせる必要があります。例えば「穴」が1つだけある場合には元々の外側の接線線積分の向きが1つの方向から見て反時計回りであれば、内側の「穴」を作る閉曲線では逆向きの時計回りで考えないとストークスの定理は成立しません。
また「穴」がある場合の考察から、ストークスの定理は1つの閉曲線に対して任意の「分割」を行える事も理解できます。
曲面として「閉曲面」を考えてしまうとどうなる?
ストークスの定理において曲面は「開曲面」を考えます。
では、曲面として「閉曲面」を考えてしまうとどうなるのでしょうか?閉曲面とは球面のような閉じた曲面です。(トーラスのような図形も含めます。)
閉曲線Cを境にして2つの開曲面に分割すると、その両方に対してストークスの定理が成立します。簡単な図形的考察と計算によって、もし曲面の表側を閉曲面に対して一貫して「内側から外側に向かう向き」と決めるなら、「閉曲面全体を積分領域とした時の、ベクトル場の回転の法線面積分の値は必ず0になる」という別の公式が得られます。
証明その1:積分と偏微分の計算を直接進める方法
ストークスの定理を数学の解析学的に「厳密に」証明する方法もありますが、考え方が非常に複雑で物理学等への応用とのつながりも見えにくいものです。そこで、ここでは比較的シンプルに考える2つの証明方法を説明します。
証明時の偏微分の計算の扱い方
ストークスの定理の証明を考える時には偏微分の扱いに特に注意する必要があります。
例えば、「偏微分をしてできた偏導関数」を積分する場合には、x、y、zが独立変数であるという条件下で計算した偏導関数がまずあります。
ベクトル場の各成分であるスカラー関数についての偏微分です。
もしyで偏微分するなら、xとzは定数扱いになります。 $$F_1(x,y,z)に対して\frac{\partial F_1}{\partial y}=\frac{\partial }{\partial y}F_1(x,y,z)=\frac{\partial F_1(x,y,z)}{\partial y}$$ そのような偏導関数があるなかで、
特定の曲面S上での法線面積分を考える時に初めてz=z(x,y)という従属関係ができます。
つまり、計算としては「偏微分を行った後の関数に対して、積分をする時点でz=z(x,y)を代入する」といった形になります。
変数をどのように考えるのかを敢えて強調して書くなら、積分時には次のようになります。 $$偏導関数\frac{\partial F_1}{\partial z}(x,y,z)に対してz=z(x,y)を代入して\hspace{5pt}\frac{\partial F_1}{\partial z}(x,y,z(x,y))$$
他方、F1(x,y,z)に対して
「曲面S上にあるという条件」を初めから課すとします。
具体的には1つの変数がz=z(x,y)という関数の形になり、
スカラー関数全体は F1(x,y,z(x,y))のように書けます。
そこで例えばyによる偏微分を行うとどうなるでしょうか?
この場合には、先ほどの場合とは計算結果が変わるのです。
偏導関数は異なる形になるのです。
その場合には、yの変化によるF1の第3成分(z成分)の変化も生じ、
それによるF1全体の変化も変わってしまうという事です。
しかし、実はその事がまさにストークスの定理の数式的な意味の1つになっています。
分かりやすくするために、具体的なスカラー関数をてきとうに考えてみます。
例えばF(x,y,z) =x2+y2+z2であったとしましょう。3変数が互いに独立なら、これを例えばyで偏微分すれば偏導関数は2yになります。xとzは定数扱いです。
それに対して、同じ関数に対してz=3yという条件がついたとしましょう。この時にはF(x,y,z) =F(x,y,z(y))=x2+y2+(3y)2=x2+10y2ですから、yで偏微分すれば偏導関数は20yになりますから全く異なる結果です。その違いが生じるのは、z=3yという条件によりyを変化させるとzも変化するためです。その違いが計算結果に現れます。
合成関数の偏微分公式で考えても同じになります。
z=3yという条件下ではF(x,y,z)を偏微分すると次のようになります。
$$\frac{\partial F}{\partial y}=\frac{\partial }{\partial y}F(x,y,z(y))$$
$$=\frac{\partial F(x,y,z)}{\partial y}\frac{\partial y}{\partial y}+\frac{\partial F(x,y,z)}{\partial z}\frac{\partial z(y)}{\partial y}$$
$$=\frac{\partial F(x,y,z)}{\partial y}+\frac{\partial F(x,y,z)}{\partial z}\frac{\partial }{\partial y}(3y)$$
$$=2y+2z\cdot 3=2y+2\cdot 3y\cdot 3y=2y+18y=20y$$
この式で、F(x, y, z) と書いた部分は3変数が互いに独立である場合の関数という意味です。その部分においては、yで偏微分するならxとzは定数扱いになるという事です。
スカラー関数の線積分の計算
ベクトル場の第1成分(x成分)であるF1(x,y,z)を考えます。これはスカラー関数で、スカラー場とみなせます。まず、接線線積分において内積をとってスカラー場の線積分の形にした積分についてまず考えます。
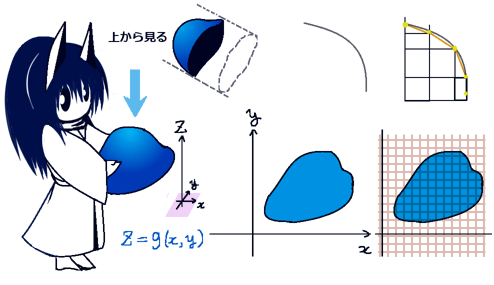
閉曲線Cは凹凸のない形状を考え、閉曲面Sはxy平面上の1点に対してz座標が1つ決まるような形状で、表側の面からの法線ベクトルはz軸のプラス方向の向きに対して鋭角になるものとします。
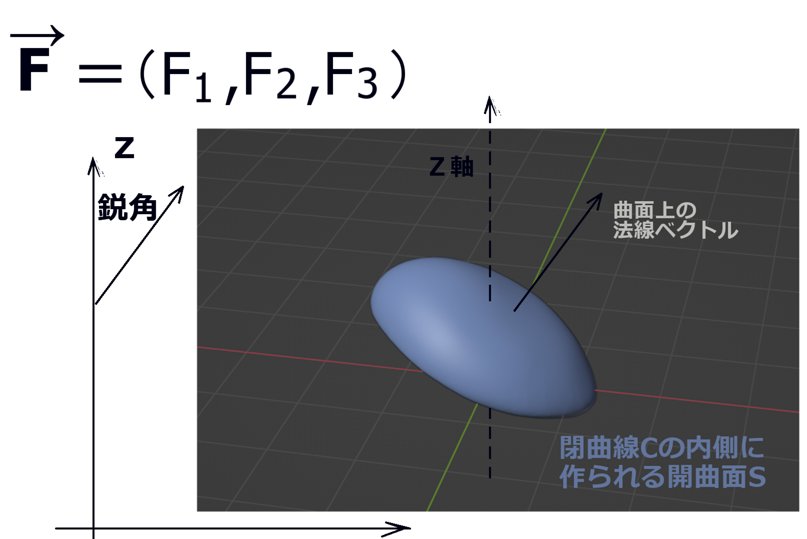
次に曲面の「xy平面への射影」を考えます。これは積分領域の射影を考えるのであって、ベクトル場の射影(つまりz成分を無視する)では無い事に注意。
ベクトル場に関しては、zに対して「積分領域の曲面の式」であるz=z(x,y)を代入する事で見かけ上zを消去します。のちに偏微分の計算をする時にはこのzの式は重要になってきます。
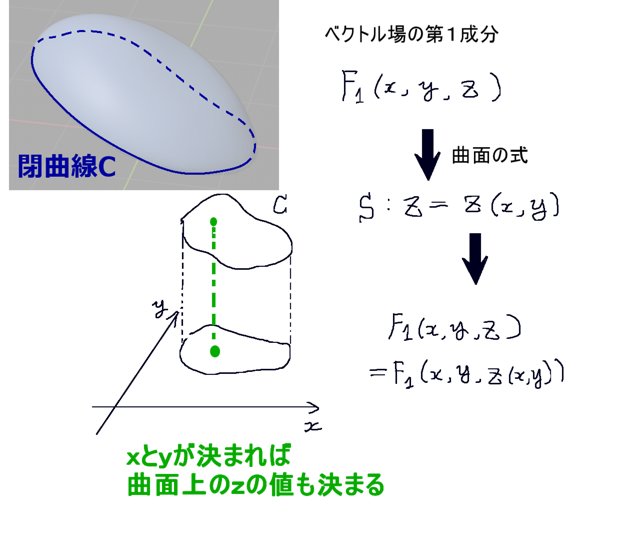
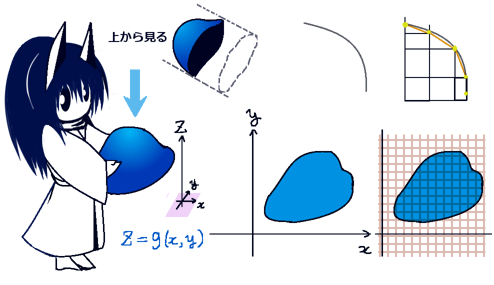
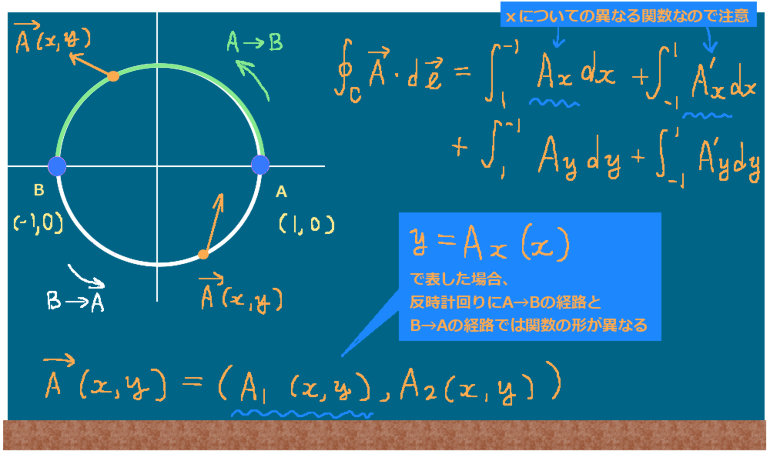
具体的な定積分(1変数の定積分)を考えようとする時、全体の射影された積分の経路に対してxについての異なる形の2つの関数が必ず存在します。これは、元々の曲線として必ず「閉曲線」を考えるためです。
xy平面で考えると、「上半分」と「下半分」に分かれる事になります。
ここでは経路を表す曲線を表す関数に対して、
xy平面上で見た閉曲線の上半分を表す場合には添え字のU、
下半分を表す場合には添え字のLをつける事にします。
また、射影されたxy平面上の閉曲線をCxy(ベクトル場の第1成分 F1 を F1xy(x,y,z(xy)) とします。)
その上半分の経路をCxU(そこではF1 を F1xyU(x,y,z(xy)) とします)
下半分の経路をCxL(そこではF1 を F1xyL(x,y,z(xy)) とします)
という名前にしておきます。
積分変数xの積分区間は [a, b] (=CxP)であるとして、線積分を行う時には反時計回りに回るようにして「行き」と「帰り」があるので往復を考えた便宜的な長方形状の経路をCxPRとしてます。
- Cxy:閉曲線 C をxy平面上に射影してできた閉曲線上 F1 =F1xy
- CxU:閉曲線Cxyの「上半分」(積分の方向は b→a)F1 =F1xyU
- CxL:閉曲線Cxyの「下半分」(積分の方向は a→b)F1 =F1xyL
- CxP:xに関する積分区間 [a, b] (閉曲線Cxyのx軸への射影)
ストークスの定理においては「閉曲線内」も計算上考えますが、その場合も平面(例えばxとy)の位置における「閉曲面上」のベクトル場だけを考えます。そのため、元々のベクトル場F1(x,y,z)において互いに独立になり得る変数は1つだけです。最初に想定した曲面の形では例えばxy平面上の点を指定すればzの値も定まるので、曲面上の値を考える時にはF1=F1(x,y,z(z,y))の形になっています。
偏微分の計算上、3変数を独立したものとして扱う場合にはF1=F1(x,y,z)と書く事にします。
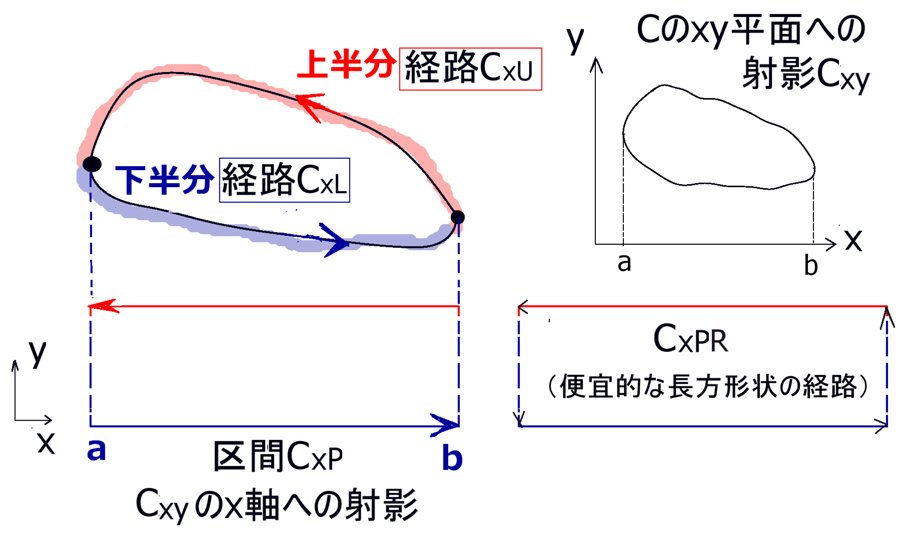
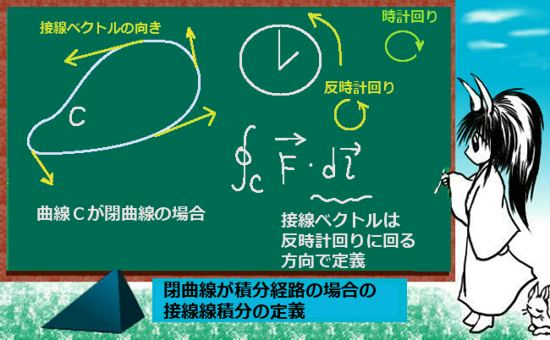
現在考えている条件下では、xy平面を上から見て反時計回りに回る方向が接線線積分の向きです。
そのため、閉曲線Cをxy平面に射影した曲線の下側が「xが増加する向きで積分する部分」であり、
上半分側が「xが減少する向きで積分する部分」になります。
まずはxy平面で考えるわけですが、1変数による線積分を行う場合に限っていえば積分変数がxであればxz平面への射影でも同じ事になります。つまり3次元空間内に閉曲線がある時、積分経路としては元の閉曲線が指定されていれば1変数の線積分の積分区間は確定します。そのため、1変数の線積分の積分経路に関しては統一的に元の閉曲線Cで表記する事にします。
$$\int_{Cxy} F_{1xy}(x,y(x),z(x,y))dx=\int_C F_{1xy}(x,y(x),z(x,y))dx$$
次に、開曲面Sに対して、xy平面上でz=(x,y)と考えます。
さらにx軸上の区間では曲線の「上半分」と「下半分」に分ければそれぞれに対してy=y(x)の関係を考える事はできますからベクトル場の第1成分F1はxだけの式で表現できる事になります。
「上半分」と「下半分」でy=y(x)の式の形も違いますから
それを強調してここでは上半分に関してはy=yU(x)などと書き、
下半分に関してはy=yL(x)のように書く事にします。
$$\int_C F_{1xy}(x,y(x),z(x,y))dx$$
$$=\int_a^bF_{1xyL}(x,y_L(x),z_L(x))dx+\int_b^aF_{1xyU}(x,y_U(x),z_U(x))dx$$
$$=\int_a^bF_{1xyL}(x,y_L(x),z_L(x))dx-\int_a^bF_{1xyU}(x,y_U(x),z_U(x))dx$$
$$=-\int_a^b\left(F_{1xyU}(x,y_U(x),z_U(x))-F_{1xyL}(x,y_L(x),z_L(x))\right)dx$$
積分区間をa→bの向きに統一して1つの積分記号に収めて、次の計算のために「上半分」のほうが前に来るように順序を変えています。
閉曲線としてまとめて積分経路を考えている時(ここで言えばCxyなど)には積分の方向が変わる時点でxの関数としての形も変わるものとして考えています。
「偏導関数の定積分」を考える
次に積分の中身で差の形になっている部分を、引き算の形である事に注目して
yに関する偏微分を使った「偏導関数の定積分」で表す事を考えます。
(※「偏微分の定積分」と言っても同じ意味になりますが、ここでは関数である事を強調して「偏導関数の…」と表現しています。)
発想的にはガウスの発散定理での証明と同じになります。
数式の意味が分かっていれば省略可能ですが「xだけの関数」と「互いに独立であるxとyが変数の関数」である事を区別するために、ここでは前者の場合のアルファベットをキャピタルで、後者を小文字で書く事にします。
つまりF1xyU(x,y(x),z(x))=f1xyU(x,y,z(x,y))であり、F1xyL(x,y(x),z(x))=f1xyL(x,y,z(x,y)) であるとします。
さきほど計算を進めた積分の中身だけで考えると次のようになります。積分区間はそれぞれのxによって定まる2つのyなので、便宜的にY1(x)からY2(x)までであるとします。yが閉曲線の内部を動く事になり、そこではF1=F1xyS(x,y,z(x,y))と書く事にします。
$$【前述の式の積分の中身】F_{1xyU}(x,y_U(x),z_U(x))-F_{1xyL}(x,y_L(x),z_L(x))$$
$$=\int_{Y2(x)}^{Y1(x)}\frac{\partial}{\partial y}\left\{f_{1xyU}(x,y,z_U(x,y))-f_{1xyL}(x,y,z_L(x,y))\right\}dy$$
$$=\int_{Y2(x)}^{Y1(x)}\frac{\partial}{\partial y}F_1(x,y,z_(x,y))dy$$
※ここでのyによる積分の計算は、閉曲線上ではなく「閉曲線の内側」を横断する形です。
(ただしベクトル場は曲面上にあります。)
yの値によって変化するF1を積分するので。xとyは従属では無く独立の関係です。xによって定まるのは「yによる積分区間の端点」だけになります。積分変数はあくまでyですから、定積分の値を直接計算するならxとzを定数扱いにしてyで偏微分したのちzにz=z(x,y)を代入して計算し、定積分の値の結果は「xだけの関数」という事になります。
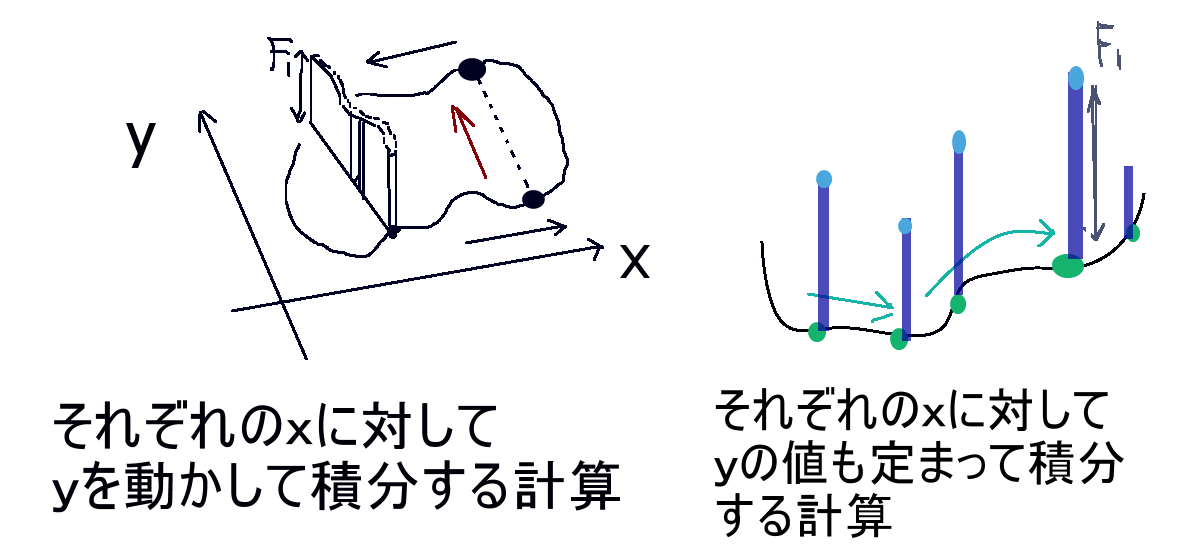
これを、既に導出している線積分の計算式に当てはめます。最初の式から考えて書き直し計算を進めると、次のようになります。偏微分の計算および面積要素の変換公式を使用します。
【偏微分については、ここではF1(x,y,z)のように書かれていたら3変数を独立変数的に扱うものと考えます。つまりyで偏微分するなら残りの変数は定数扱いという意味での計算式になります。】
$$\int_C F_{1xy}(x,y(x),z(x))dx$$
$$=-\int_a^b\left(\int_{Y2(x)}^{Y1(x)}\frac{\partial}{\partial y}F_1(x,y,z(x,y))dy)\right)dx$$
$$=-\int_a^b\int_{Y2(x)}^{Y1(x)}\left(\frac{\partial F_1(x,y,z)}{\partial y}\frac{\partial y}{\partial y}+\frac{\partial F_1(x,y,z)}{\partial z}\frac{\partial z(x,y)}{\partial y}\right)dxdy$$
$$=-\int_{Sxy}\left(\frac{\partial F_1(x,y,z)}{\partial y}+\frac{\partial F_1(x,y,z)}{\partial z}\frac{\partial z(x,y)}{\partial y}\right)ds_z$$
$$=-\int_{Sxy}\frac{\partial F_1(x,y,z)}{\partial y}ds_z -\int_{Sxy}\frac{\partial F_1(x,y,z)}{\partial z}\frac{\partial z(x,y)}{\partial y}ds_z$$
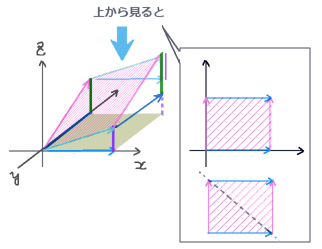
$$=-\int_{Sxy}\frac{\partial F_1(x,y,z)}{\partial y}ds_z +\int_{Sxz}\frac{\partial F_1(x,y,z)}{\partial z}ds_y【∵面積要素の変換公式】$$
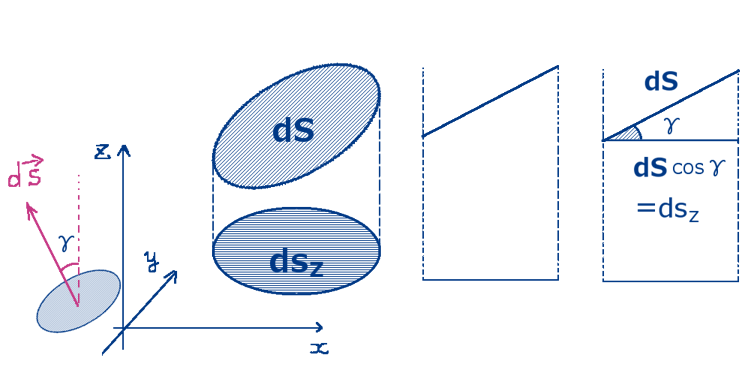
ここで使った面積要素の変換公式はあまり使う機会のない公式ですが次のような形のものです。【※重積分の変数変換の公式とは別物なので注意。】
$$面積要素の変換公式:ds_y=-\frac{\partial z(x,y)}{\partial y}ds_z$$
xy平面とxz平面の面積要素がこの式に従って1対1に対応するので積分領域もxy平面からxz平面に移る事になります。
まとめると次のようになります。
$$\int_C F_1(x,y(x),z(x))dx$$
$$=-\int_{Sxy}\frac{\partial F_1(x,y,z)}{\partial y}ds_z +\int_{Sxy}\frac{\partial F_1(x,y,z)}{\partial z}ds_y$$
これは、接線線積分の側から見た時の内積の項の1つを表す式になっています。同様の手順でyとzによる線積分からも同様の結果が得られ、全て加え合わせる事でここでの閉曲面の設定におけるストークスの定理が導出されます。

証明の計算の流れのまとめを図示すると次のようになります。
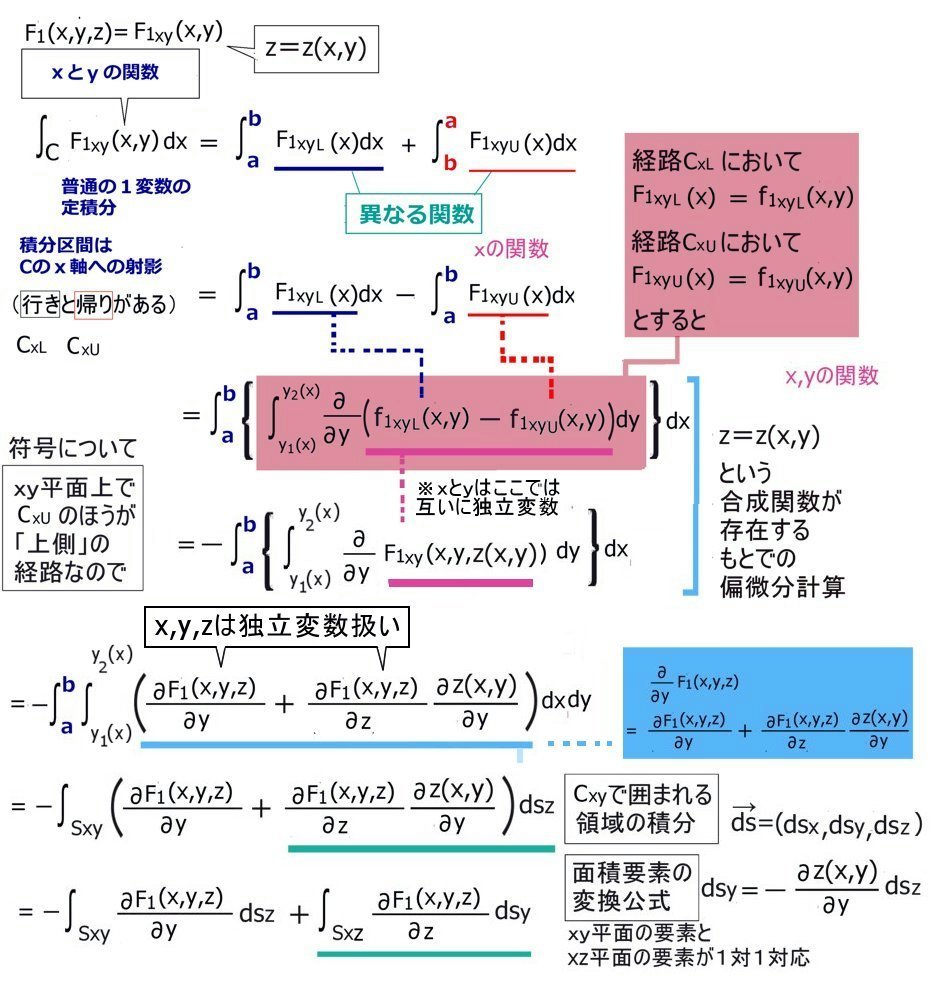
この証明では積分の領域は開曲面Sに依存するのではなく、閉曲線Cに依存するものとなっています。しかも、より正確には閉曲線Cのxy平面等への「射影」の領域に依存しています。つまり定理において開曲面Sの形状は任意でよい事も示せています。
曲面が変化すればその曲面上のベクトル場の具体的な関数形は当然一般的には変化しますが、式の形自体は閉曲線Cの形状に縛られず自由であるという事になります。(最初は変数に従属関係があったのが、最後はあたかも独立変数として扱う計算となったのはこの事に関係があります。)
もちろんここではまだ特定のタイプの曲面に限っての話です。次に、開曲面がここで考察したもの以外の別の形状でも成立する事を見ます。
曲面の形状が変わった時
では、閉曲面Sが最初に設定したもの以外の場合はどうでしょうか。
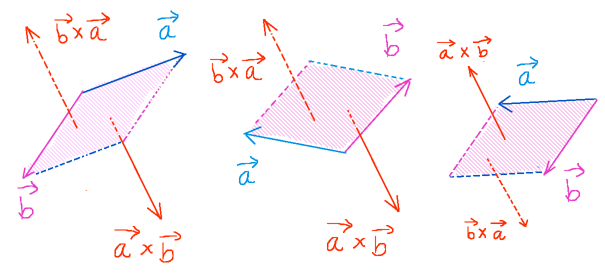
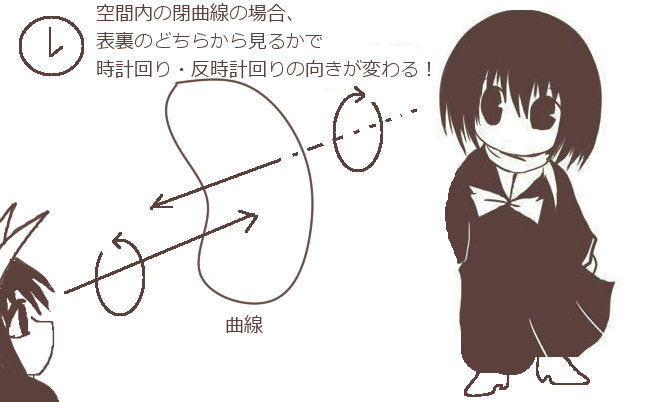
まず、「開曲面Sの表裏が入れ替わった場合」です。
その場合、まず接線線積分の積分方向が逆回りになるので、内積で分解した時の線積分も計算結果の符号が入れ替わったものになります。
他方でその場合には例えばxy平面への射影を考える時に、元々は曲面Sの1つの方向から出る法線ベクトルが逆向きになります。つまり、元々がdsz=+dxdyであれば、曲面の裏表を入れ替えた時にはdsz=-dxdyという変換になります。
すると前述の証明と比較した場合、証明の過程で符号の反転が2回起こるので、「結果は同じになる」という事になります。
また、先に「穴がある場合」でも定理が成立する事は既に見ましたが、そこで考察した分割の方法によって、曲面が任意の形状であっても既に証明済みのタイプに細かく分割して積分値を合計する事で定理が成立する事を示せます。
じゅうたんを折り畳んだような複雑な曲面によって、面積要素ベクトルが他の場所と符号が変わる場合も定理は成立します。この場合には面積要素ベクトルは依然として「表」から出ている事にはなりますが、分割をすると裏表を変えた時のように接線線積分の向きが逆になる事が分かります。従って、裏表を変えた時と同様に定理は成立します。
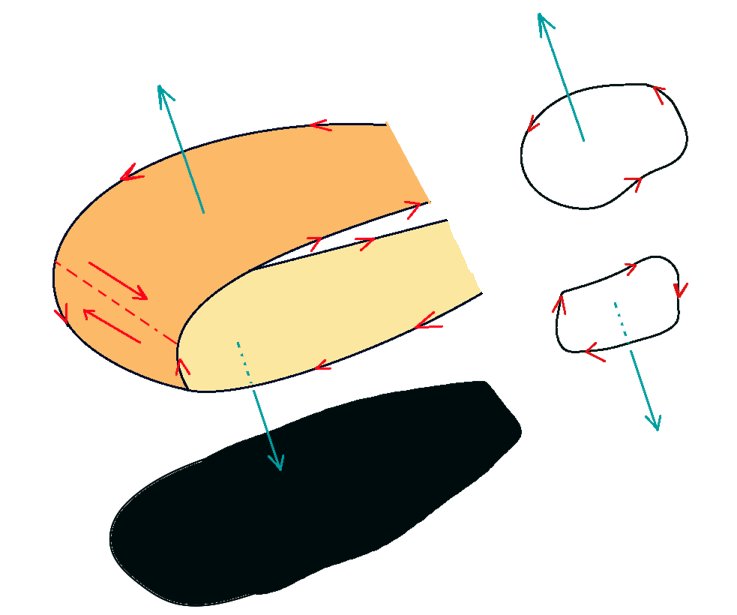
証明その2:微小長方形領域で回転を計算する方法
別の証明方法として、ベクトル場の「回転」をより図形的な回転のイメージに合わせたやり方があります。
この方法では閉曲線のxy平面等への射影領域を、軸に平行な線でメッシュのように「細かい長方形に分割する事」で証明を行います。ただし、それは斜めの線を長方形に強引に近似できるという意味ではありません。そうではなくて、接線線積分や法線面積分の内積を利用した計算によって「結果的に長方形領域の組み合わせで計算ができる」という事です。
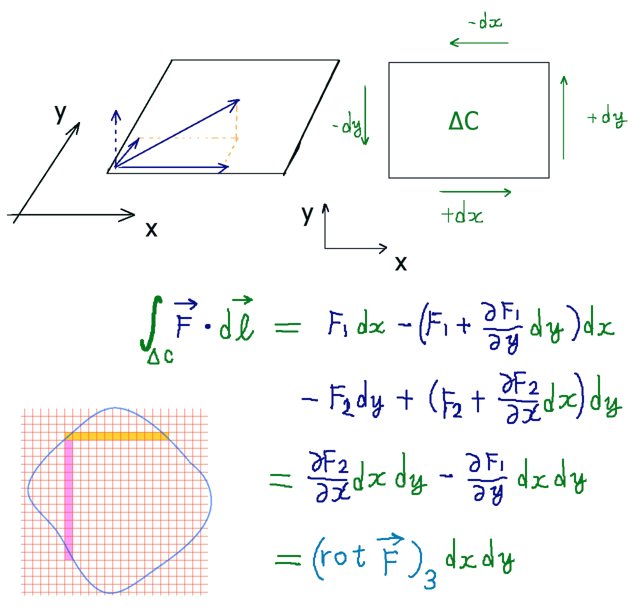
まず最初に、少し奇妙に思えるかもしれませんが閉曲線のxy平面を最初にメッシュ状に細かく分割してしまって、それから1つの微小な長方形領域ΔCに対してベクトル場との「接線線積分を行うかのような和」を考えます。つまり、積分の方向を決めたうえで各辺をベクトルと考えた時のベクトル場との内積をとり、合計するという事です。ただし、微小領域なので1つの辺につきベクトル場の値は1つだけで代表できると考えます。
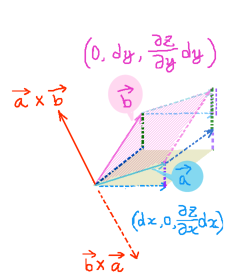
この時に、ベクトル場は3成分ともx,y,zのプラスの方向を向いている条件であるとします。すると、長方形領域ΔCはxy平面上の図形であるわけですからz成分は0です。さらには軸に平行な線で作られた長方形ですから辺をベクトルとみなせば成分はx成分のみかy成分のみという事になります。
長方形領域ΔC辺の長さをdxとdyとすると、
4つの「接線ベクトル」はz成分を省略してそれぞれ
(dx,0),(0,dy),(-dx,0),(0,-dy)です。
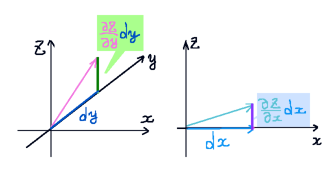
長方形の左端にベクトル場があって、微小の長さを進んで偏微分を使った一次近似の量だけ増えるものとします。少し奇妙なようですが、ベクトル場との内積をとって合計すると次のようになります。
$$\oint_{\Delta C}\overrightarrow{F}\cdot d\overrightarrow{l}=F_1dx+\left(F_2+\frac{\partial F_2}{\partial x}dx\right)dy-\left(F_1+\frac{\partial F_1}{\partial x}dy\right)-F_2dy$$
$$=\left(\frac{\partial F_2}{\partial x}-\frac{\partial F_1}{\partial x}\right)dxdy=\left(\mathrm{rot}\overrightarrow{F}\right)_3dxdy$$
$$\left(\mathrm{rot}\overrightarrow{F}\right)_3はベクトル場の回転の第3成分$$
つまり、回転するように「接線線積分もどき」のようなものを考えると、「ベクトル場の回転」の成分(ここでは第3成分)に面積要素を乗じた量になったわけです。このように最初から「回転のイメージ」が現れるところが先ほどの証明方法と異なる点です。
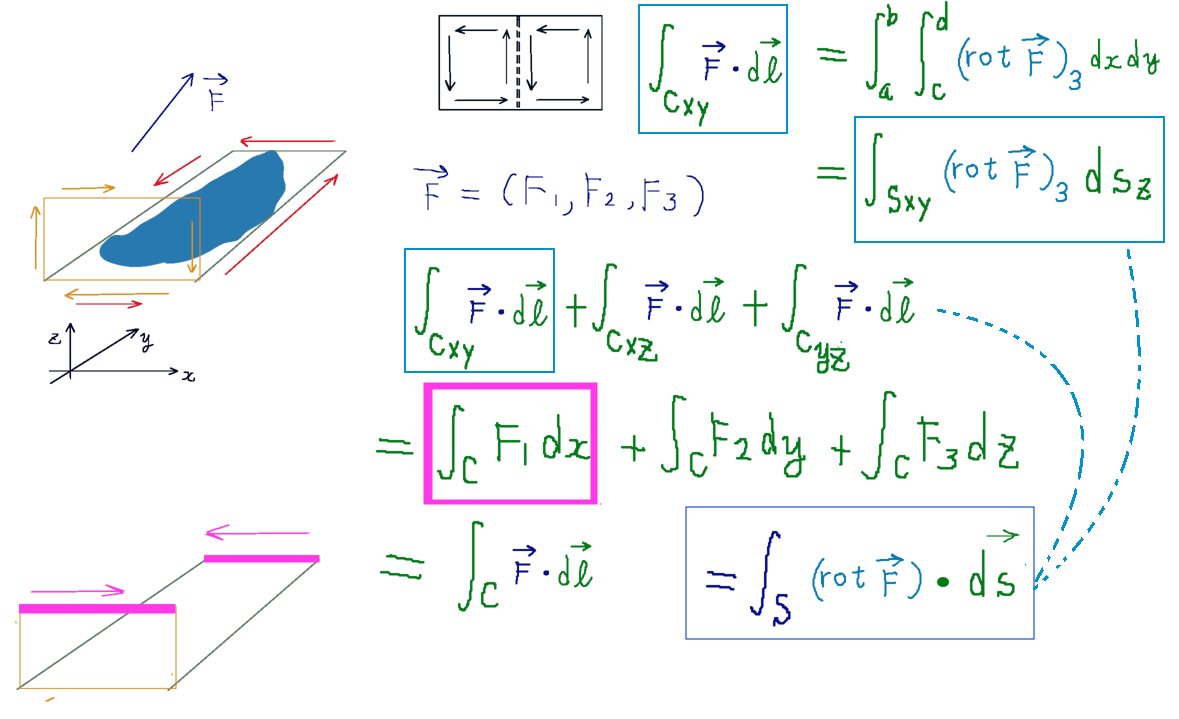
xとyについて積分すれば、ベクトル場の回転の法線面積分の第3成分を得ます。同様の方法で残りの成分も得る事ができます。それで、ストークスの定理の法線面積分側の式ができあがるわけです。
$$3成分について積分して合計すると\int_S\mathrm{rot}\overrightarrow{F}\cdot d\overrightarrow{s}を得る。$$
さてそれでは接線線積分側はどうでしょうか。
メッシュ状に細かく分割した長方形に対してさきほどの式を合計すると、隣り合う辺においては値が打ち消し合って消えます。領域の分割の逆のパターンで、積分する領域の合成が行われるわけです。
すると、長方形を全部合成すると外部の周に相当する部分だけが残ります。これで接線線積分を内積計算した時の1変数の線積分が出てきます。
しかし、じつは単純に計算するとxy平面に対してxの線積分とyの線積分が生じて、xz平面でもxの線積分とzの線積分の両方が生じてしまい謎の「過剰な量」が出てきてしまいます。
ですが注意深く見てみると、xの線積分を行う場所は合計で4箇所できますがそのうちの2つは「同じ線分上で向きだけが異なる線積分」となるので合計すると0になります。そして残り2つで、xに関する線積分の「行き」と「帰り」を表現できているのです。
つまり、一見すると線積分の項が6つできて往復を考えると12項ができてしまいますが半分は打ち消して0になるので1変数の線積分の項が3つでそれぞれに積分区間の往復がある形になります。これで接線線積分側の式も得られてストークスの定理を導出できる事になります。
$$\oint_{Cxy}\overrightarrow{F}\cdot d\overrightarrow{l}+\oint_{Cxz}\overrightarrow{F}\cdot d\overrightarrow{l}+\oint_{Cxy}\overrightarrow{F}\cdot d\overrightarrow{l}$$
$$=\int_CF_1dx+\int_CF_2dy+\int_CF_3dz=\oint_C\overrightarrow{F}\cdot d\overrightarrow{l}$$
$$\oint_{Cxy}\overrightarrow{F}\cdot d\overrightarrow{l}+\oint_{Cxz}\overrightarrow{F}\cdot d\overrightarrow{l}+\oint_{Cxy}\overrightarrow{F}\cdot d\overrightarrow{l}=\int_S\mathrm{rot}\overrightarrow{F}\cdot d\overrightarrow{s}により$$
$$\oint_C\overrightarrow{F}\cdot d\overrightarrow{l}=\int_S\mathrm{rot}\overrightarrow{F}\cdot d\overrightarrow{s}$$
設定した形状のタイプ以外の開曲面に対しても成立する事を調べるのは最初の証明と同じです。この2番目の証明では、閉曲線Cの射影となる領域だけで考えて定理を導出しています。言い換えると必要な射影を与える開曲面であれば形状は任意でも定理が成立するので1つの閉曲線を外縁とする開曲面は任意で良いという事になります。