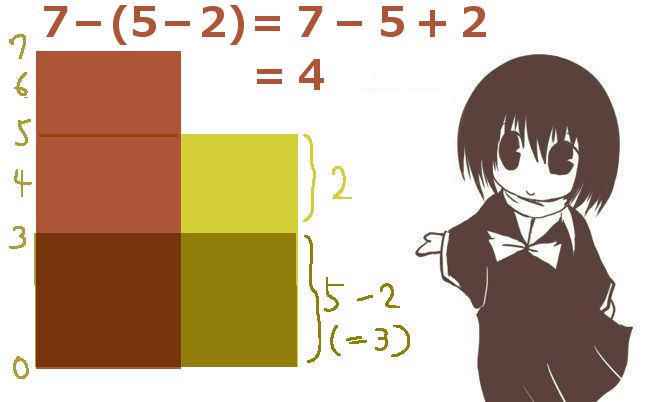「学校での数学の勉強方法は、一体どうしたらよいか?」「数学の成績を伸ばすにはどうしたらよいか?」
こういった事はよく聞かれるので、中学や高校での実践的な勉強法について紹介します。
実践的な勉強法を知り、身に付けよう
よく耳にする「勉強方法」としては、授業の予習復習を欠かさない・1日1時間でも30分でも勉強時間をとる・塾に通う・・等々というものです。これらについて私が聞いていて思うのは、科目の内容には直接的に言及しない一般論が極めて多いという事です。
それらの一般論は間違っているわけではありませんが、よい勉強方法というよりは「成績が良い子の特徴」を拾って列挙しているという面が結構強いのではないかと思います。もっと言うと、数学をあまり知らない人でも、成績優秀者にアンケート調査すれば分かる事を列挙しているようにも聞こえるのです。
よくある一般論的な「勉強方法」
- 毎日の勉強時間の確保(例えば1時間でも30分でも)
- 授業をただ受けるのではなく予習と復習を必ずする
- 塾や予備校に通う
- 将来の夢を明確にする事で勉強への意欲を高める 等
→ 正しい事も言っているが「現に成績が良い子」の特徴の列挙にとどまっている面もあり、成績改善のための根本的な指南にはなりにくい。指摘の範囲が広すぎて具体性を欠いている事も否定できない。
それらの一般論が間違っているわけではなく、時に重要性もある事は強調したうえで、ここではより実践的で実際の数学にも踏み込んだ形でのおすすめできる「勉強方法」について紹介したいと思います。
ここで述べる事は、数学が得意でない人が成績を伸ばすために役立つ事でありますが、すでにある程度得意な人が成績に伸び悩み行き詰った時や、さらに上を目指したい場合にも役立つ方法です。(上記のような一般論だと、予習や復習はしているけれど成績が伸び悩んでいる人などは対処のしようがなくなってしまいます。)
実際に中学校や高校に通っていると勉強や進路に関して難しい事もあろうかと思いますが、まずは学校の数学の授業で教わっている内容が一体何なのかを把握しましょう。それが正直よく分かっていない状態で、「試験があるので公式だけは暗記する」・・というのは一番危険な勉強法です。これは中学でも高校でも、数学の勉強に関して共通に言える事なのです。
数学公式を覚えるために「語呂合わせ」(社会科だと『いい国【1192】作ろう鎌倉幕府』などが有名)を使う事を勧める人もたまにいらっしゃいますが、それを絶対否定はしませんが、その方法はどうしてもどうやっても覚えられない時の最終手段だと思う事をここでは勧めます。そうではない方法についてここでは述べます。
数学の成績を伸ばす手段の1つとして「多くの練習問題を解いてみる」という事は有効な方法です。ただし、それは基礎事項がある程度分かっている(完璧でなくても)時に先に進む手段として効力を発揮するもので、解き方の原理が全く分かっていない状態で練習問題に取り組んでも効果が薄いのです。
従って、数学があまり得意でない場合には、まず基礎事項を把握する事から始めるのが第一歩です。この時、公式だけを見て暗記しようとするのではなく、その公式の意味の説明や解説をよく読み、最初は自分で解かなくてもいいのでどういった計算例などがあるのかをよく見るようにしましょう。
完璧に理解してなくてもいいので、何となくでも分かったら、簡単なものからでよいので練習問題を解いてみてください。そして計算の方法などが分かってきたら、入試問題の過去問題を解いてみるなどしてレベルを上げて行きます。
中学・高校ともに共通する勉強法として大事な事は、わけもわからずに漫然と問題に手をつける事を繰り返すのではなく、基礎事項を理解したうえで問題を多く解くという事です。それによって、基礎事項の理解もより深まるのです。
個々の具体的な基礎事項を勉強する時には教科書や参考書を見てもいいですし、このサイトでは数学の基礎・重要事項についてイラストや図式も使いながら詳しく分かりやすく解説しています。
それらの押さえておくべき基礎事項を分野ごとに具体的に把握し、整理しておく事も重要です。これについては、中学数学・高校数学等に分けて次に具体的に記していきましょう。
★「基礎」とは必ずしも「簡単」という意味では無く、土台になる部分という事です。ただし中学校や高校の範囲では、基礎事項とは「まずは簡単な事項・初歩的な事項」というふうに捉えても差し支えありません。
中学校での勉強法
中学校の数学であれば、まずはマイナスを含んだ式の計算、文字式の展開、文字式の因数分解といったものを教わり、試験にも出題されます。(この試験とは期末試験などの校内のものも、高校入試も含みます。)
中学校の場合、公立の高校入試であれば(どの都道府県でも)おおよそ出題範囲は決まっており、おおよそ次のようなものです。
中学校の数学で扱う基礎・重要事項
- マイナス符号の扱い(マイナス同士の掛け算など)
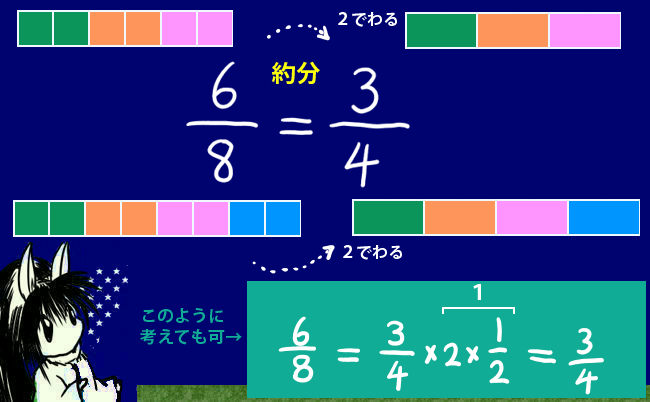
- 文字式の展開と因数分解
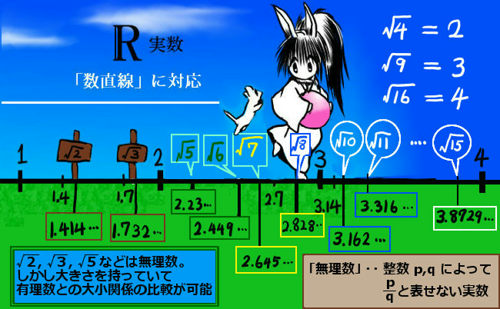
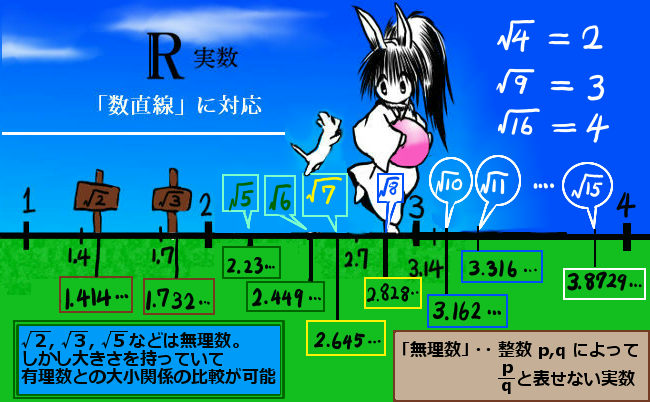
- 平方根の扱い(分母の有理化など)
- 方程式(1次方程式、1次の連立方程式、2次方程式)
- 2次関数と1次関数のグラフ問題(交点など)
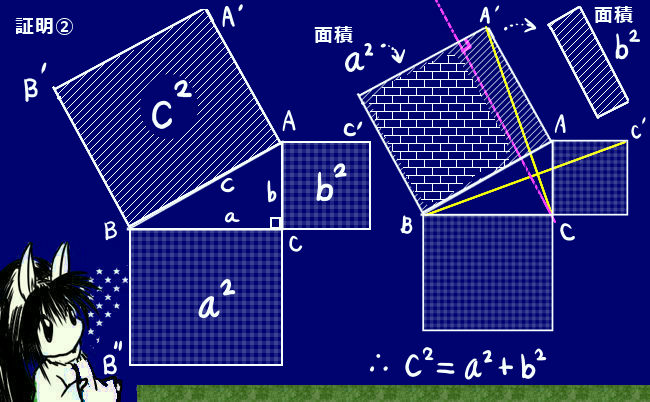
- 図形問題(作図、相似や合同の証明、辺の比・面積計算)【証明問題の勉強法については後述】
- 初歩的な確率の問題(サイコロを2回ふるなど)
- 統計(最頻値・中央値などの用語を把握したうえでのグラフの読み取り)
- 立体に関する計算問題(展開図や平面での切り口)
- 一部、自然数・整数に関する問題(約数、倍数、素数、個数の数え上げなど)
具体的な問題は、例えば次のようなものです。
「-2+5はいくらか」「(-2)×(-3)+1はいくらか」
「(x-2)(x-5) を展開しなさい」
「x2-7x+10を因数分解しなさい」
などのような問題が解ければ、身もふたもない事ですが「数学の成績が上がる」わけです。
※公立高校の入試の場合、多くの都道府県で求められるのはこういうレベルの計算です。ただし学校によっては入試でそれが「正確に」(速く)解ける事が求められます。
ここで、個々の生徒の人によって、問題を見て思う事が違うでしょう。
「暗算レベルですぐに答えられる」
「紙に書いて落ち着いて計算すれば解答を出せる」
「やり方は一応分かっているけれど計算間違いをよくしてしまう」
「そもそも何をどうすればよいのか分からない」
計算は人によって得意不得意あるので解けないからといって悪い事は何もないのですが、成績を上げるにはどうすればよいかという観点からは、まずは当人がどのような理解度にあるのかを把握する事が第一歩です。
これは、本人が自分で気づけば一番良いですが、それができない場合には大人が指摘してあげる事も大事なのです。実際、塾や家庭教師、通信教育の中には、そういった適切な指摘をしながら問題演習を通じて成績向上に導いていくという手法をとっている場合もあります。がむしゃらに問題を解かせるというのも成績向上の手法として否定はしませんが、それは前述のように、あらかじめ一定の理解度のある生徒にとってさらに成績を伸ばすために有効な方法です。
先ほどの問題ですが、-2+5=3ですが、これは結局5-2と同じで、
「足し算と引き算は本質的に順序を入れ替えてもよい」「引き算は『マイナスの数を加える』とみなしてよい」といった事が分かっている前提があるわけです。
次に (-2)×(-3)+1=7ですが、
これは「マイナス同士の掛け算はプラスになる」事と、
「掛け算と割り算は、足し算・引き算よりも優先して行う」という規則を知っているかを問うているわけです。つまり(-2)×(-3)を先に計算して6にする必要があるわけで、-3とその右隣の1を先に掛けたりしてはいけないわけです。【(-2)×(-3+1)の場合には-3+1を先に計算します。】
因数分解の問題の場合には、まずはその逆である式の展開について分かっていて計算もできる事が重要です。x2-7x+10=(x-2)(x-5) ですが、これをすぐに計算できるようにするためには因数分解とは逆の
(x-2)(x-5)=x2-7x+10 という式の展開計算が問題なくできるという前提があります。
そういった点を見落とさず、整理する事が基礎事項を押さえるという事の1つの具体例です。
大事なのは、まずは生徒である本人がそういった計算における「ルール」を正確に知っているかどうかです。知っているのであれば、あとはひたすら問題を多く解いて計算の精度と速さを上げていくという勉強方法は確かに成績向上につながります。しかし正直よく分かっていない状態で、なかば当てずっぽう的に問題を解く事を繰り返している状況になっている場合には一度立ち止まる事も必要です。
結果的に言えば、成績の良い子は多くの公式を暗記してるはずだと思います。しかしそれは、公式の意味や使い方は把握しているうえで、練習問題を通して慣れる事によって記憶を定着させている事が普通なのです。
あやふやな点がある・正直よく分かっていないところがあるという場合は、問題は解かなくていいので基礎にもどりましょう。そこで内容の理解に努めてから、簡単な問題からでいいので練習してみて、分かってきたら問題集や過去問によって速く・正確に解けるように繰り返し解いてみましょう。【速く解ける事は、見直しの時間を確保したり、多少手間がかかる出題があった時に落ち着いて考える時間を確保する事に役立ちます。】
高校入試の場合、公立高校やそれに準じるレベルの私立高校の場合は「難問・奇問」は出さず、基礎事項さえ正確に把握していれば確実に解けるレベルの出題をしている場合が大半です。一部の「難関私立校」を受験したいと思う場合でも、基本問題は確実に速く解けるという事はまず必要であり、そこからさらにやや難しい問題を解く練習を積む事が勧められます。
次に、中学校の数学の中でも「証明問題」に対する勉強はどのように考えたらよいのかについて、少し述べておきます。
証明問題に対する勉強法
中学校に入ると「証明」問題というものが出てきます。これは確かに、一見すると小学校の算数との大きな違いです。
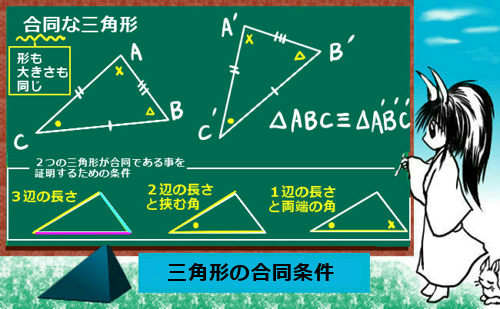
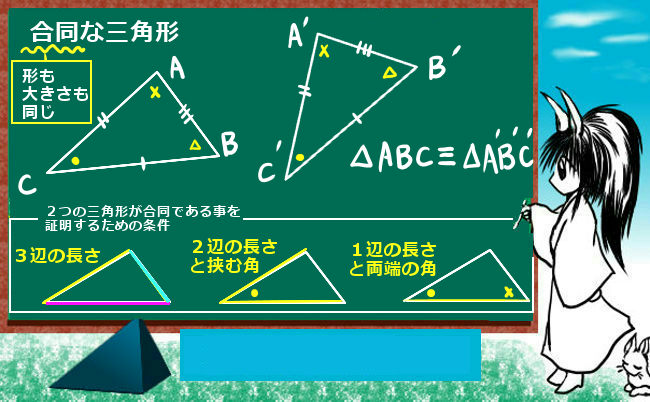
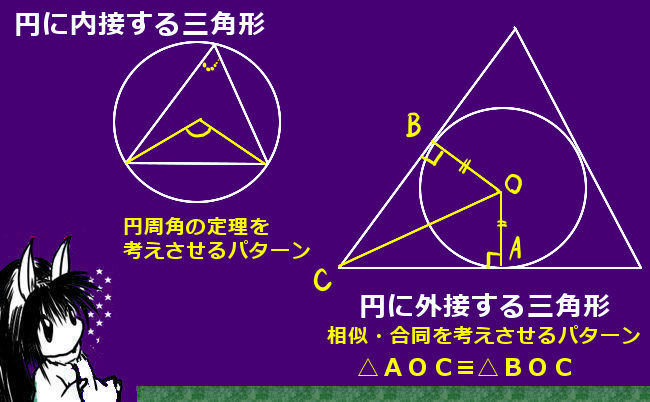
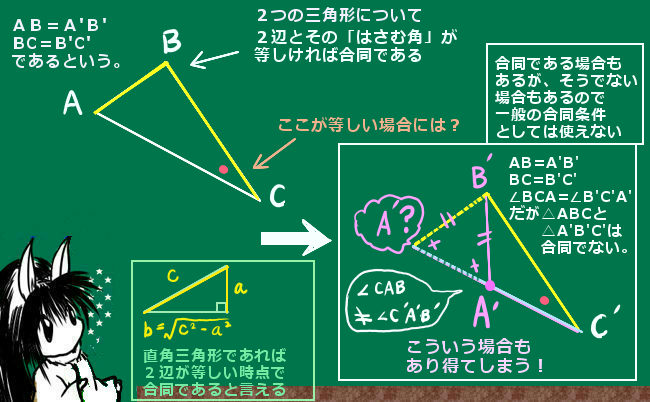
中学校で証明問題というと大抵は図形問題かと思います。これを得意にするためには、基礎となる定理や条件を整理して理解したうえで、入試の過去問題や練習問題を繰り返し解いて練習してみる事が有効です。
ですから基本的には他の計算問題と勉強法は同じというわけです。
大事な事は、問題を一気に解決してくれるような裏テク的な「特別な定理」を探そうとしない事です。
最も基礎になる定理だけをまず理解して整理し、具体的な問題に使う時はどうすればよいのかを問題を解きながら理解し慣れていく事が大事です。
押さえておくべき基礎的な定理や図形の性質は、具体的には次のようなものです。
覚える事項をこういった基礎事項に絞ったうえで、練習問題や過去問題によって使い方を練習していくのが勧められる勉強法です。問題はいくらでも異なるものがありますが、大抵の場合はパターンが限られています。
一部の私立高校の入試などで他に事項が必要と思われる時のみ、過去問題を精査したうえで特別な定理を覚えればよいでしょう。もちろん、入試の受験などを抜きにして、平面幾何の分野に興味を持った場合に教科書に載っていない色々な定理を調べてみるという事は何ら悪い事ではありません。
証明問題について、「論述」をする必要があるという事で苦手意識を持つ人もいるかもしれません。しかし、数学の証明は国語の作文や小論文とは根本的に異なるものです。そのため普段の勉強においても、数学の証明は国語の問題や試験とは全く違うものである事をまずおさえておく必要があります。
数学の証明問題は、読み手を説得させる文章を書く事が目的ではなく、
「数学的に論理的に正しい関係をつなげて(決まった)結論を出す」というだけのものです。
ここで、「論理的に正しい」という事には文学的な意味も哲学的な意味もなく、要するに正しい計算をしているか・正しい定理の内容を書いているか・図形問題であれば正しい辺と角度の関係を書いているかという事なのです。
高校での勉強法
高校数学の場合、難関の国立大・私大の入試で「奇抜」な問題が出題される事があるのでその事に目を奪われがちかもしれませんが、中学校の場合と同じく基礎事項を整理し把握したうえで練習問題・過去問題を使って練習する事が最も勧められる勉強法です。高校の学内の期末試験等の対策も同じになります。
大学入試の場合には個々の大学によって出題傾向や難易度の差が激しい場合もあるので、確かにひとくくりにできない面はあります。しかし、基礎事項を正確に把握している事はどこの大学の入試でも求められます。したがって、普段の勉強でも特殊な問題や「難問」を無理に解く訓練をするのではなくて、まずは基礎事項を組み合わせて解ける問題を確実に解けるようにする事が勧められる勉強法です。つまり基本姿勢は中学校の時と同じでよいのです。
数学科目で高校が中学校と異なる点は、勉強する範囲が広いのでいきなり全ての対策を一度にはできない事です。範囲が広いので、場当たり的に勉強してしまうとつい学習が不足している部分が出てきやすいのです。分かりやすいところからでいいので、1つ1つの分野を確実に把握していく事が重要と言えるでしょう。
高校数学の微積分以外の分野で知っておくべき基礎・重要事項は次のようになります。
高校数学の基礎・重要事項
- 直交座標上の図形と式(1次関数、2次関数、円、軌跡)【3次関数は主に微分の分野】
- 数列(等差数列、等比数列、漸化式、階差数列、数学的帰納法)
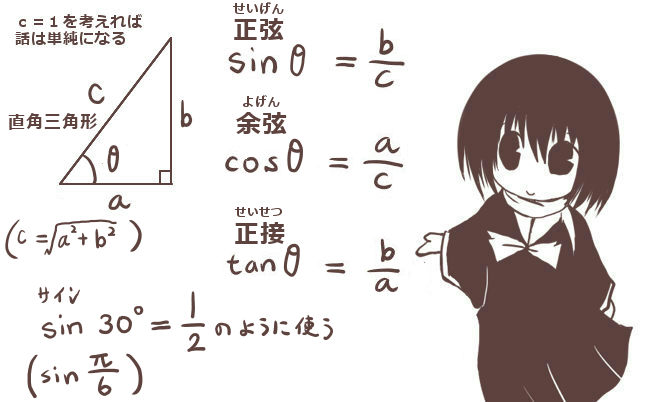
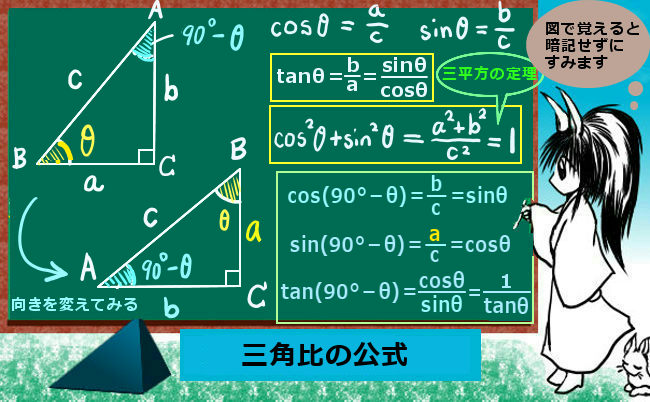
- 三角比と三角関数(基本公式、弧度法、余弦定理、加法定理、極座標)
- ベクトル(基本事項、内積、座標上の平行四辺形の面積など)
- 集合と論理(包含関係、必要・十分条件、対偶証明法、背理法など)
- 指数関数と対数関数
- 場合の数と確率(順列、組み合わせ、条件付き確率、期待値、分散など)
- 統計(中学よりも範囲が少し広い)
- その他小さい事(絶対値記号、和の記号(Σ)、二項定理、解と係数の関係、部分分数、中間値の定理など)
- 行列(基本的に2次の正方行列に関する出題が多い)
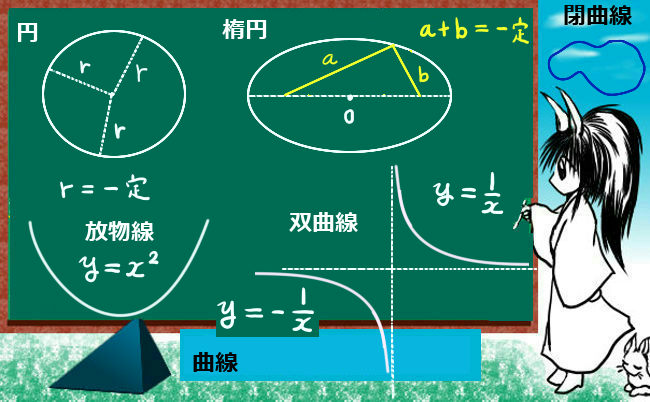
- 2次曲線(楕円、双曲線、一般の放物線)
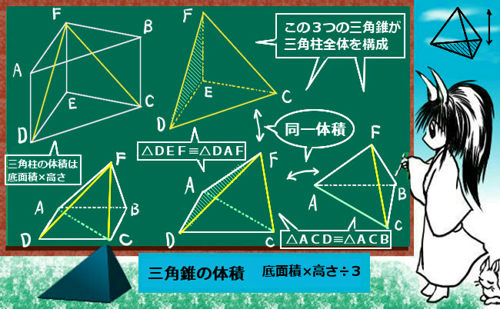
★高校の場合、立体に関する問題は積分で体積を計算させる出題が比較的多いです。
★様々な分野がありますが、最終的には全く別々の切り離されたものではなくて互いに関係しているという事を意識する事も重要かと思います。
高校数学では数学を授業科目として3~6つに分類する事が多いですが、学習時にはあまりこういう分類にはこだわらずに「微積分」と「それ以外」くらいの分類の認識でもよいかもしれません。微積分の問題を解く場合にはそれ以外の事項の基礎知識が欠かせない場合も多いので、まずは「微積分以外」の分野をしっかり勉強しておく事が重要とも言えます。
高校数学では、どうしても「問題が解けない(解答にたどりつかない)」という場合が中学の場合と比べて多く発生すると思います。そういう時には、勉強の1つのコツとして、問題の「解答」を先に見てしまってください。
すると、じつは意外に簡単で基本的な基礎事項をいくつか組み合わせるだけの問題であったりします。それを知ったうえで、再度問題を解いたり他の問題にも手をつけてみて、そういったレベルのものであれば確実に解けるように練習を積んでみる事が勧められます。解答を見ても基礎事項の組み合わせで済むとは到底思えない「難問」の場合は、普段の勉強においても後回しにして放置して大丈夫です。
まずは、基礎事項とその組み合わせからなる問題を確実に・正確に・速く解けるようにしましょう。
基礎事項がよく把握できていない場合は、落ち着いて分からない部分について一度基礎事項を整理し、内容の把握に努めましょう。この時、公式や定理だけを見て暗記しようとしない事が中学校の時以上に重要です。例えば三角関数の分野1つだけとってみても非常に多くの「公式」があり、無理に暗記しようとしても中学の時以上に相当厳しいものがあると思います。
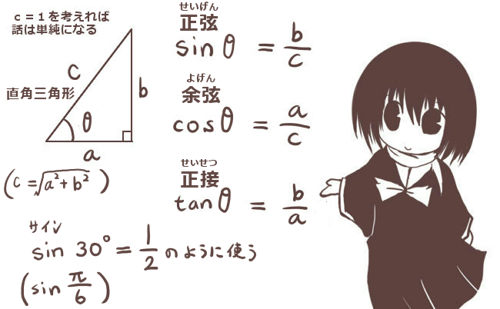
暗記しないでどのように覚えるのかと言われるかもしれませんが、例えば三角関数で言えば正弦と余弦の公式を把握していれば正接の公式は計算で出せますし(その関係自体、重要事項です)、
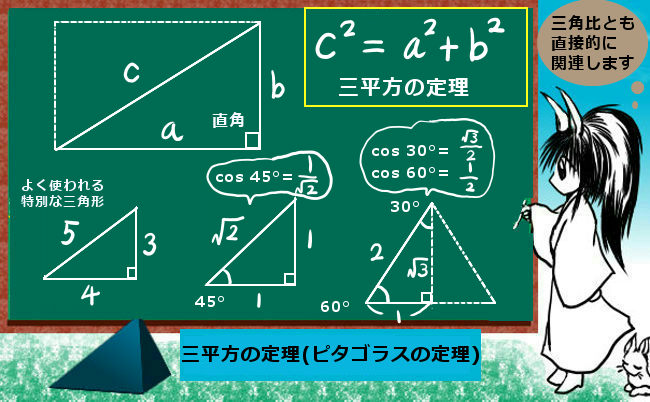
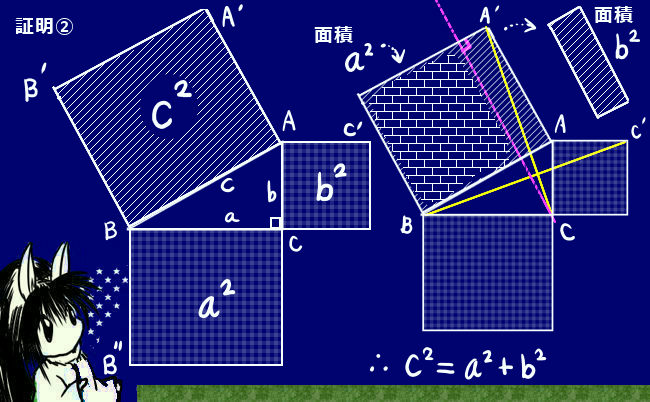
sin2θ+cos2θ=1という基本公式は本質的には「三平方の定理」である事を理解していれば「暗記」の負担は相当に減るでしょう。余弦定理の場合、角度が直角である場合は三平方の定理に他ならない事を知っておけば、定理の内容の大半は全く新規のものではなく既に知っているという事になります。
このように、全ての定理や公式を全く別物と捉えるのではなくて、数学的な関連付けをする事で結果的に暗記する項目を減らせるのです。
そういった「整理された基礎事項の知識」を練習問題や入試問題を解く中でアウトプットしていく事を積み重ねていくと、数学の知識は定着し成績は伸びていきやすいかと思います。
高校数学の場合には「基礎」を正確に押さえる段階に至るまでが、中学の時と比べて労力を要するという面があるかもしれません。その事をあらかじめ踏まえて普段の勉強に取り組むと効率よい学習が可能でしょう。
高校数学の学習で特に気を付けるべき点
- 高校数学では教わる内容の範囲が広い。(それぞれ無関係ではなく関連はある。)
- 公式や定理の数も多く、相互の分野の関連付けをしないと基礎知識の整理が難しい場合もある。
微積分が出題範囲の時
大学の理系の学部の入試では微積分まで問われる事が多いと思います。
微積分の範囲まで学習する場合には、微分の場合には関数の極大・極小を調べてグラフを描く問題、積分の場合には面積・体積を計算する問題が比較的多く、合成関数や積の微分公式、置換積分・部分積分の公式なども合わせて使う場合もあります。また一部、特定の関数の極限を計算させる出題などもあります。
勉強法としては微積分以外の分野と同じように考えます。
ただし微積分に関しては、まず基本になるのが微分のほうで、その計算に慣れてきたら積分のほうに移れるという性格が強いです。(これは積分は微分の逆演算であるという性質によります。)また三角関数や指数関数の知識など、微積分以外の分野の正確な理解が必要な事も多いです。そのため、それらの理解がまだじゅうぶんでない場合には一度戻ってみる事も有効な手段かもしれません。
まとめと結び
こういった勉強法は、中学や高校だけでなく、資格取得などの時にも有効なものです。まず必要な基礎事項を詳しく整理・把握・理解し【それは「公式」の暗記ではありません】、演習問題・試験の過去問題を使って練習を積むというものです。
数学の成績を伸ばすために勧められる勉強法について以上の事を整理しておきます。
まとめ
- 数学を勉強する時には、まずは基礎知識を大事にしよう
- 出題範囲を整理して、勉強不足の分野がないようにしよう
- 公式や定理を無理に暗記するのは避け、内容の理解に努めよう
- 基礎知識がある程度理解できたら、その知識が完璧でなくてもいいので練習問題や入試の過去問題を解いてみるようにする。それによって知識が定着する。
- 理解が不足している場合にはもう一度基礎知識の整理に戻る
- 出題範囲が広い・公式の数が多いといった時には相互の数学的な関連を理解する等の、何らかの工夫が必要がある場合もある
- 高校数学でどうしても解答が出せない場合は解答を見てしまうのも1つの手。基礎知識の組み合わせで解ける事も多く、それを知る事自体が勉強になる。それを踏まえて改めて問題を解くようにする。
大学数学の場合は、必ずしも問題を解く事が学ぶ目的ではないのですが、大学によって試験で高得点をとる事・問題を解く事を重視する方針であるというのであれば、やる事は高校までの勉強法と同じです。
(個人的には、問題を解くという事に関しては多くの人が高校までにじゅうぶんやってきていると思うので、大学ではもう少し学問や研究をするという意味での勉強に重点を置いたほうがよいのではないかという気はいたします。)